Pytorch Note46 生成对抗网络的数学原理
Posted 风信子的猫Redamancy
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Pytorch Note46 生成对抗网络的数学原理相关的知识,希望对你有一定的参考价值。
Pytorch Note46 生成对抗网络的数学原理
全部笔记的汇总贴: Pytorch Note 快乐星球
之前介绍了什么是生成对抗,接下来会用严格的数学语言证明生成对抗网络的合理性。
详细也可以查看GAN的论文Generative Adversarial Networks
首先介绍一下KL divergence,这是统计学的一个概念,用来衡量两种概率分布的相似程度,数值越小,表示两种概率分布越接近。
分别有离散的概率分布和连续的概率分布,定义如下。
-
离散的概率分布
D K L ( P ∣ ∣ Q ) = ∑ i P ( i ) log P ( i ) Q ( i ) D_{KL}(P||Q)=\\sum_{i}P(i)\\log\\frac{P(i)}{Q(i)} DKL(P∣∣Q)=i∑P(i)logQ(i)P(i) -
连续的概率分布
D K L ( P ∣ ∣ Q ) = ∫ − ∞ + ∞ P ( x ) log p ( x ) q ( x ) d ( x ) D_{KL}(P||Q)=\\int_{-\\infty}^{+\\infty}P(x)\\log\\frac{p(x)}{q(x)}d(x) DKL(P∣∣Q)=∫−∞+∞P(x)logq(x)p(x)d(x)
其实本质我们是想将一个随机的高斯噪声 z z z通过一个生成网络 G G G得到一个和真的数据分布 p d a t a ( x ) p_{data}(x) pdata(x)差不多的生成分布 p G ( x ; θ ) p_{G}(x;\\theta) pG(x;θ),其中参数 θ \\theta θ是网络的参数决定的,希望找到 θ \\theta θ使得 p G ( x ; θ ) p_{G}(x;\\theta) pG(x;θ)和 p d a t a ( x ) p_{data}(x) pdata(x)尽可能接近。
可以用下面这张图说明
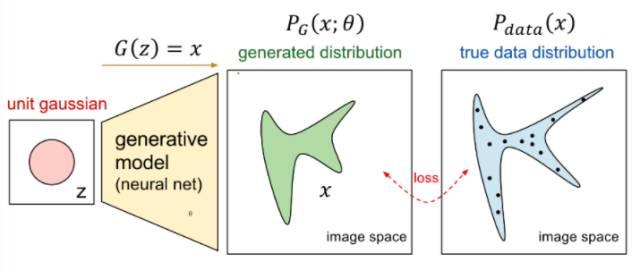
从论文来看,接着我们会从真实数据分布
P
d
a
t
a
(
x
)
P_{data}(x)
Pdata(x)里面取样
m
m
m个点,
{
x
1
,
x
2
,
…
,
x
m
}
\\{x^1,x^2,\\dots,x^m\\}
{x1,x2,…,xm},根据给定的参数
θ
\\theta
θ 可以计算概率
P
G
(
x
i
;
θ
)
P_G(x^i;\\theta)
PG(xi;θ),那么生成
m
m
m 个样本数据的似然 (likehood)就是
L
=
∏
i
=
1
m
P
G
(
x
i
;
θ
)
L=\\prod_{i=1}^{m} P_{G}\\left(x^{i} ; \\theta\\right)
L=i=1∏mPG(xi;θ)
接着我们需要找到
θ
∗
\\theta^{*}
θ∗ 来最大化这个似然估计:
θ
∗
=
arg
max
b
∏
i
=
1
m
p
G
(
x
i
;
θ
)
⇔
arg
max
θ
log
∏
i
=
1
m
P
G
(
x
i
;
θ
)
=
arg
max
θ
∑
i
m
log
P
G
(
x
i
;
θ
)
≈
arg
max
θ
E
x
∼
P
theta
[
log
P
G
(
x
;
θ
)
]
⇔
arg
max
θ
∫
x
P
dota
(
x
)
log
P
G
(
x
;
θ
)
d
x
−
∫
x
P
data
(
x
)
log
P
data
(
x
)
d
x
=
arg
max
θ
∫
x
P
data
(
x
)
log
P
G
(
x
;
θ
)
P
data
(
x
)
d
x
=
arg
min
θ
K
L
(
P
data
(
x
)
∣
∣
P
G
(
x
;
θ
)
)
\\begin{aligned} \\theta^{*}&=\\arg \\max _{b} \\prod_{i=1}^{m} p_{G}\\left(x^{i} ; \\theta\\right) \\Leftrightarrow \\underset{\\theta}{\\arg \\max } \\log \\prod_{i=1}^{m} P_{G}\\left(x^{i} ; \\theta\\right) \\\\ &=\\underset{\\theta}{\\arg \\max } \\sum_{i}^{m} \\log P_{G}\\left(x^{i} ; \\theta\\right) \\\\ &\\approx \\underset{\\theta}{\\arg \\max } E_{x \\sim P_{\\text {theta }}}\\left[\\log P_{G}(x ; \\theta)\\right] \\\\ &\\Leftrightarrow \\underset{\\theta}{\\arg \\max } \\int_{x} P_{\\text {dota }}(x) \\log P_{G}(x ; \\theta) d x-\\int_{x} P_{\\text {data }}(x) \\log P_{\\text {data }}(x) d x \\\\ &=\\underset{\\theta}{\\arg \\max } \\int_{x} P_{\\text {data }}(x) \\log \\frac{P_{G}(x ; \\theta)}{P_{\\text {data }}(x)} d x \\\\ &=\\underset{\\theta}{\\arg \\min } K L\\left(P_{\\text {data }}(x)|| P_{G}(x ; \\theta)\\right) \\end{aligned}
θ∗=argbmaxi=1∏mpG(xi;θ)⇔θargmaxlogi=1∏mPG(xi;θ)=θargmaxi∑mlogPG(xi;θ)≈θargmaxEx∼Ptheta [logPG(x;θ)]⇔θargmax∫xPdota (x)logPG(x;θ)dx−∫xP