论文阅读|Info2vec: An aggregative representation method in multi-layer and heterogeneous networks

Posted 白鳯

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了论文阅读|Info2vec: An aggregative representation method in multi-layer and heterogeneous networks相关的知识，希望对你有一定的参考价值。

论文阅读|Info2vec: An aggregative representation method in multi-layer and heterogeneous networks

文章目录

Abstract

将多层网络中的节点映射到低维向量在社区检测、节点分类和链路预测等方面有广泛应用。首先将异构网络通过图变换得到聚合网络，根据不同层的网络结构生成潜在的信息链接。然后通过聚合节点的结构、接近度和属性等信息，对聚合网络中不同节点之间的相似度进行综合度量。 基于节点具有的综合相似度值，可以使用边缘渗透方法生成上下文图，它为一些重要的下游工作（如分类、聚类和预测等）提供了基础。

Introduction

同一层中的节点，由于其属性不同，可能存在不同的类别。从skip-gram模型发展来的方法有，学习节点的广义表示，然后根据获得的表示向量执行一些下游任务（如分类、聚类、检测等）。

网络中的表征学习侧重于将原始图数据转换为低维向量，同时从结构、接近度和属性等角度保留图的内在属性。这种低维向量允许通过计算来广义理解两个节点之间的相似性，如表示向量之间的欧几里得距离或余弦相似度，以及促进进一步的下游分析。表示向量可以通过使用不同的方法获得，包括降维、矩阵分解和神经网络等。节点嵌入基于随机游走的算法已被广泛使用。

现有表示学习可分为以下三个分支：

  • 侧重于接近度的相似性，如deepwalk（该方法在处理稀疏数据、缺失信息和并行计算的情况下具有优势，应用于网络分类和网络检测，但无法使远离根节点但功能相似的节点建立联系）。Node2vec（深度游走的通用版本，能够学习来自同一社区的节点以及共享相似角色的节点的表示）
  • 同时考虑近邻相似性和结构相似性。如struc2vec（计算层次结构中任意两个节点之间的相似度，然后构造一个加权的多层图来生成节点序列，最后使用skip-gram模型来学习潜在表示。该方法需要大量的计算资源，并且无法捕捉到近邻之间的相似性）
  • 归纳学习强调邻居以及高阶邻居的聚合节点的属性。如GraphSAGE（利用节点特征并将它们合并到学习过程中来训练一组聚合器函数，基于这些函数可以生成看不见的节点的嵌入。 通过将邻域信息与节点特征相结合，该方法在预测节点分类或动态图中的角色方面优于传统基线）

Info2vec从结构、接近度和属性的不同角度聚合信息，以实现更准确的预测。其贡献有：

  • 通过聚合来自不同层的信息将多层异构网络转换为单层网络的方法，使得焦点层上的节点可以与来自支持层的信息很好地连接。
  • 通过考虑领域相似性、结构相似性和属性相似性来引入广义表示学习框架，以通过向量表示节点。所提出的框架优于一些传统的基线方法

Graph Transformation

多层异构图表示为 G L = ( L , E ) G^L=(L,E) GL=(L,E)，其中 L = { G 1 , G 2 , . . . , G m } L=\\{G_1,G_2,...,G_m\\} L={G1​,G2​,...,Gm​}表示层集。在单层 G k = ( V k , E k , A k ) G_k=(V_k,E_k,A_k) Gk​=(Vk​,Ek​,Ak​)中，包含节点集 V k = { v 1 k , v 2 k , . . . , v n k } V_k=\\{ v_1^k,v_2^k,...,v_n^k \\} Vk​={v1k​,v2k​,...,vnk​}，边集 E k = { e i j k } E_k= \\{ e_{ij}^k \\} Ek​={eijk​}，节点 v i k v_i^k vik​和节点 v j k v_j^k vjk​通过边 e i j k e_{ij}^k eijk​连接。

令 ϕ k : v i k ∈ V k → θ i k ∈ A k \\phi _k : v_i^k ∈ V_k → \\theta _i^k ∈ A_k ϕk​:vik​∈Vk​→θik​∈Ak​表示 G k G_k Gk​层的节点 v i k v_i^k vik​具有属性 θ i k \\theta _i^k θik​，其中 θ i k = [ θ i , 1 k , . . . , θ i , t k ] \\theta_i^k = [\\theta_{i,1}^k,...,\\theta_{i,t}^k] θik​=[θi,1k​,...,θi,tk​]。

令 E = { E 12 , E 13 , . . . , E k f , . . . } E=\\{E_{12},E_{13},...,E_{kf},...\\} E={E12​,E13​,...,Ekf​,...}表示两层之间的连接。例如 E k l E_{kl} Ekl​表示层 G l G_l Gl​和层 G k G_k Gk​之间的连接，节点 v i k v_i^k vik​和节点 v j l v_j^l vjl​间的连接边表示为 e i j k l e_{ij}^{kl} eijkl​。

下图是论文中展现的多层异构图：

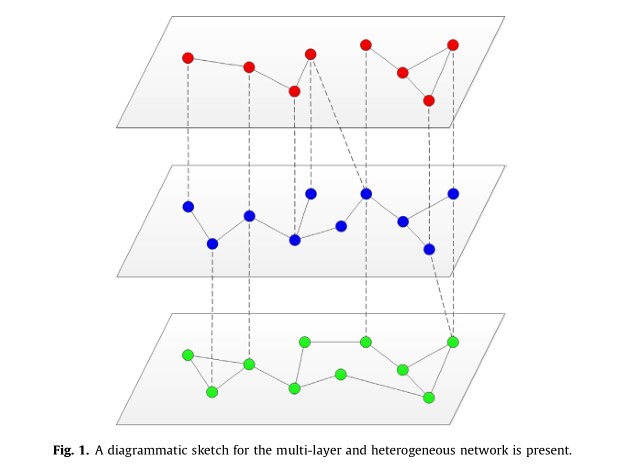
在多层异构网络中，了解支持层中结构或连接的基本信息有助于更好地理解焦点层上的活动。为准确捕获焦点层中节点的身份，需要采取措施聚合来自支持层的信息。实施图转化，将焦点层扩展为聚合网络，将焦点层的信息与支持层的信息相结合。聚合网络应包含焦点层中的所有现有边，以及一些新添加的链接。

考虑到不同网络层链路之间的相互依赖性，焦点层中的两个节点在支持层中具有共同邻居或连接到支持层中的某个边的情况下，在焦点层上更可能有密切的交互。具体来说，对于在焦点层原本没有连接的两个节点，对于以下两种不同的情况，它们之间需要在汇聚网络中建立一条新的链路：

  • 三角形连接
  • 四边形连接

由论文中图可见：

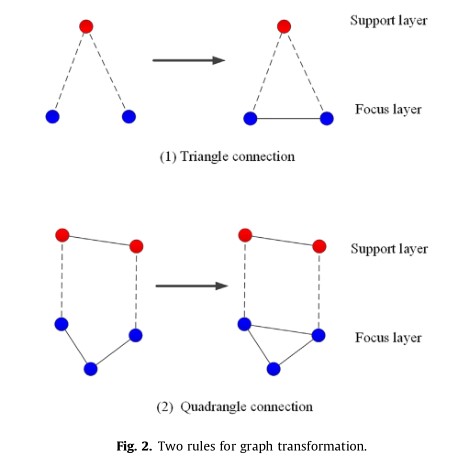
在聚合网络中，节点之间的边比焦点层中的边更密集，聚合的信息更多。图转换后的结果如下所示：

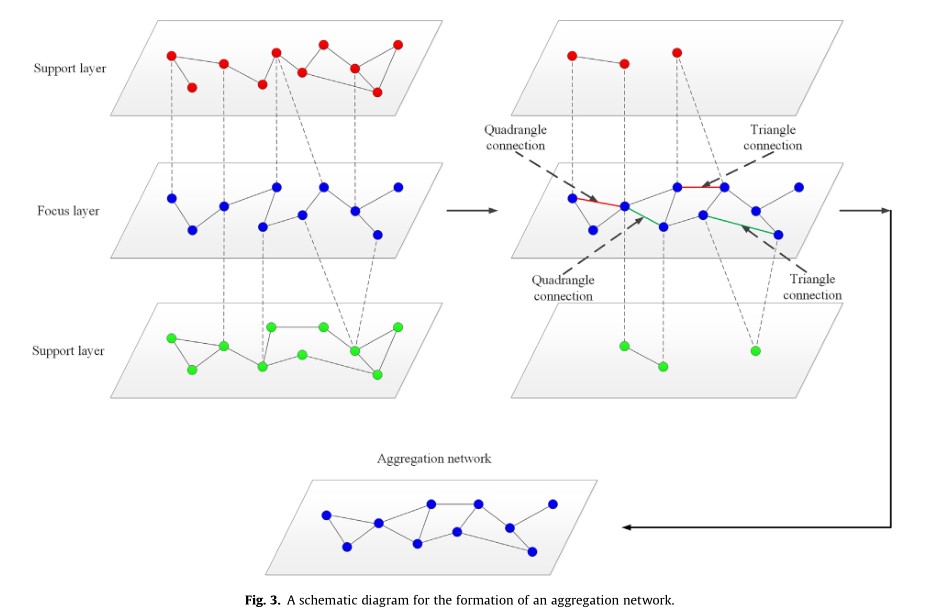
Info2vec: aggregation of information

Measuring similarity

论文采用的三种相似性度量