17.2 无监督数据增强——UDA

Posted 2021-09-08 炫云云

文章目录

• • 有监督数据增强
  • 无监督数据增强
  • 训练技巧
  • • 训练信号退火（TSA）
    • 锐化预测
    • 域相关数据过滤
  • 参考

17.1 自然语言处理中文本数据增强方法

有监督数据增强

所谓数据增强就是在保持标签一致的情况下，通过某种转换方法扩充出类似于真实数据的训练数据。简单而言就是，有一个样本$x$，通过转换函数$q（x）$生成新数据$x_a$，新旧数据有相同的数据标签。通常为了得到的增强数据与原始数据相似，使用的是最大似然估计方法。

数据增强方法可以看成是从有标签数据中扩充出更多的有标签数据，然后用扩充数据进行模型训练。因此，扩充数据相对于原始数据必须是有效的变换（例如图片缩放对图片识别可能有效，图片旋转可能无效）。也因此，如何设计转换函数至关重要。

目前，针对NLP任务的有监督数据增强方法已经取得了很大进展。虽然有成果，但是它通常被比喻成“蛋糕上的樱桃”，只是提高有限的性能，这是由于监督数据通常都是少量的。因此，本文研究了一种基于大量数据的无监督数据增强方法。

无监督数据增强

当前半监督学习中，利用无标签数据去进一步平滑模型的方法，主要归纳为以下两步：

• 有一个输入$x$,然后输出分布 $p_{\theta }(y\mid x)$, 再有一个添加了噪声$ϵ$ 的$x$, 输出分布为 $p_{\theta }(y\mid x,ϵ)$,
• 最后最小化以上两个分布的距离： $\mathcal{D}\left(p_{\theta }(y\mid x)\Vert p_{\theta }(y\mid x,ϵ)\right)$.

这个过程有两点好处：

1. 会让模型对抗噪声的能力得到提高, 当输入发生改变的时候, 输出不会发生大的变化，会比较平滑，
2. 可以把标签信息 丛标签数据传递无标签数据中。

UDA使用最小化无标签数据增强数据和无标签数据的KL散度。公式如下：
$$\underset{\theta }{\min }{\mathcal{J}}_{\mathrm{U}\mathrm{D}\mathrm{A}}(\theta )=\underset{x\in U}{E}\underset{\hat{x}\sim q(\hat{x}\mid x)}{E}\left[{\mathcal{D}}_{\mathrm{K}\mathrm{L}}\left(p_{\tilde{\theta }}(y\mid x)\Vert p_{\theta }(y\mid \hat{x})\right)\right],\text{\hspace{1em}(1)}$$
其中 $\hat{x}\sim \mathrm{q}\left(\hat{\mathrm{x}}\mid \mathrm{x}\right)$ 是数据增强变换, $\tilde{\theta }$ 是当前参数的固定副本，表明梯度不是通过 $\tilde{\theta }$传播的。这里使用的数据增强转换与监督数据增强中使用文本数据增强方法相同。由于数据增强耗时比较大，所以数据增强是离线生成的，单个原始样本会生成多个增强样本。

为了同时使用带标签数据和无标签数据，在计算带标签数据时上加上交叉熵损失和 $\lambda$​ 为权重的公式 1 , 最终公式如公式2所示，模型结构如图1所示。
$$\underset{\theta }{\min }\mathcal{J}=\underset{x,y^{\ast }\in L}{E}\left[p_{\theta }\left(y^{\ast }\mid x\right)\right]+\lambda {\mathcal{J}}_{\text{UDA }}(\theta )\text{\hspace{1em}(2)}$$

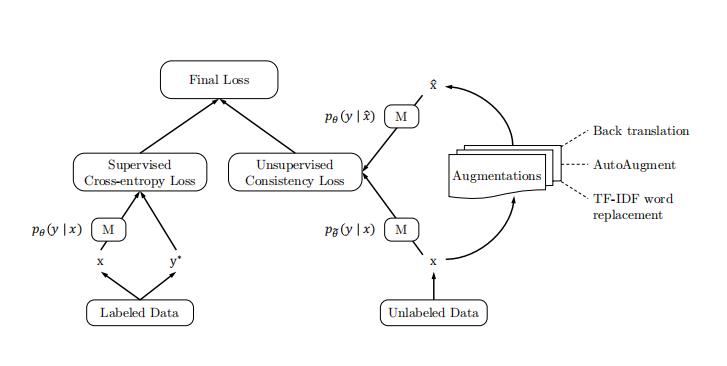
$$图1:UDA训练模型架构，其中M表示模型$$
通过最小化一致性损失，UDA能够使得标签信息从标签数据引入无标签数据。对于大多数实验，将λ设置为1，并对标签数据和无标签数据使用不同的批处理大小。并发现，在一些数据集上，对无标签数据使用更大的batch会带来更好的性能。

相比较于传统的加噪方法，例如：高斯噪声、dropout噪声、或者简单的仿射变换，对不同任务进行针对性的数据增强能够生成更加有效的噪声。它具有以下优点：

（1）扰动的有效性：让增强数据和原始数据使用相同标签在监督学习中取得了良好性能，因此，对于无标签数据的增强也是类似有效的。

（2）扰动的多样性：由于可以对输入数据进行多种方式的改动而不改变数据标签，所以数据增强具有更强的多样性，而例如高斯噪声和贝努力噪声改变了局部信息，因此多样性不好。另外，由于是在一组增强数据集上进行平滑操作，所以数据增强拥有较高的效率。

（3）定向归纳偏差：不同的任务需要不同的归纳偏差。如自动增强，数据增强策略可以直接优化以提高验证性能 每项任务。这种面向性能的增强策略可以学会在原始标记集中找出缺少的或最想要的归纳偏差。虽然自动数据增强策略是应用于监督学习任务中的，但是在本文半监督数据增强中，同样有效。

训练技巧

本节主要介绍一些针对不同问题，不同场景下的训练技巧。

训练信号退火（TSA）

TSA主要是针对标签数据与未标签数据不平衡时的场景。由于有大量的未标签数据需要UDA处理，所以需要一个较大模型，但是由于较大模型很容易在少量标签数据下过拟合，所以，提出了本方法用于解决该问题，即Training Signal Annealing（ 简称TSA)。

TSA的基本原理就是在训练过程中，随着未标签数据的增加，逐步去除带标签数据，从而避免模型过拟合到带标签的训练数据。具体而言，就是在训练的t时刻，设置一个阈值 ${\eta }_t$，当$1/K\le {\eta }_t\le 1$，其中，K是类别数。 当某个标签数据计算的$p_{\theta }\left(y^{\ast }\mid x\right)$大于阈值 ${\eta }_t$ ，就将该标签数据移除出计算损失的过程，而只计算miniBatch里面的其余数据。假定miniBatch样本记作B，那么该策略计算损失如下：
$$\underset{\theta }{\min }\frac{1}{Z}\sum _{x,y^{\ast }\in B}\left[-I\left(p_{\theta }\left(y^{\ast }\mid x\right)<{\eta }_t\right)\log p_{\theta }\left(y^{\ast }\mid x\right)\right]\text{\hspace{1em}(3)}$$
过滤后的样本集合:
$$Z=\sum _{x,y^{\ast }\in B}I(p_{\theta }\left(y^{\ast }\mid x\right)<$$

推荐 ：关于机器学习的十种常用算法

增强半监督人脸识别噪声

一种数据增强方法-非核心词替换

17.2融合关键词的文本增强

根据 Google Play 的政策，我的增强现实应用没有足够的关于家长监督的警告

增强学习 ----- 基本概念