[数值计算-8]:一元n次非线性方程求解-双点区间-弦截迭代法&Python法代码示例
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[数值计算-8]:一元n次非线性方程求解-双点区间-弦截迭代法&Python法代码示例相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119821256
目录
1.1 非线性函数
线性函数是一次函数的别称,则非线性函数即函数图像不是一条直线的函数。非线性函数包括指数函数、幂函数、对数函数、多项式函数等等基本初等函数以及他们组成的复合函数
1.2 非线性函数案例
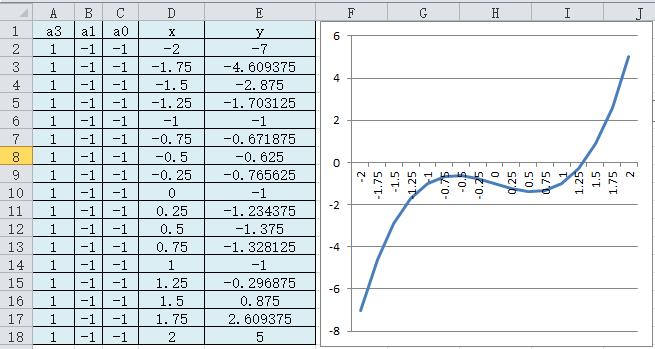
y = f(x) = a3*x^3 + a2*x^1 + a0
另a3 = 1, a2=-1, a0=-1;得到:
y=f(x) = x^3 - x - 1
1.3 非线性函数的几何图形
2. 弦截迭代法求非线性方程解的基本原理
2.1 基本思想
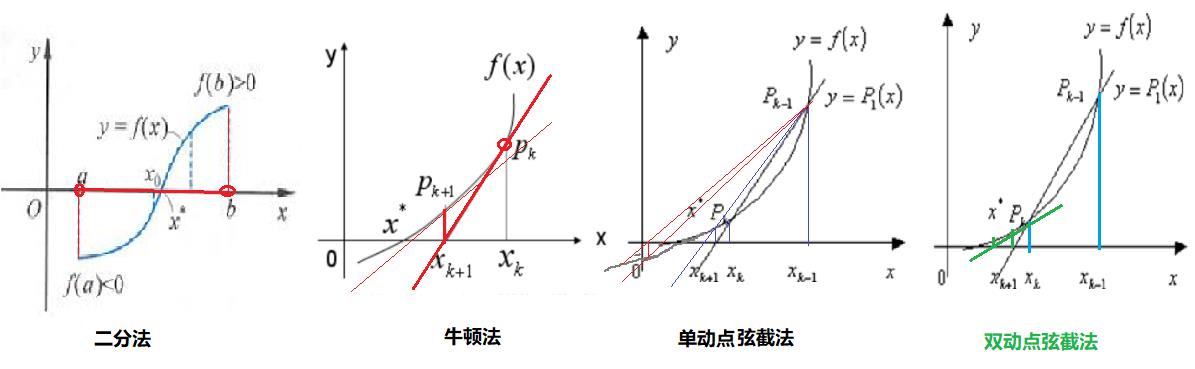
二分法:是使用一个X轴区间上的x值的二分中值点(线性)Xk值,逐渐逼近真实解X。
牛顿法:使用非线性曲线上的一个点切线(线性)与X轴的交点Xk值,逐渐逼近真实解X。
玄截法:使用非线性曲线上的二个点的连线(线性)与X轴的交点Xk值,逐渐逼近真实解X。
本质:
无论那种方法,本质上是用曲线上相关的点构成的直线方程的解(即与x轴的交点)来逼近真实的解。即用线性直线替代非线性曲线,用线性解无限逼近非线性解。
神经元的本质就是一个直线,神经网络就是大量的线性直线构逼近现实的非线性方程。



2.2 确定误差或收敛条件
与牛顿迭代法类似,用Xk+1 - Xk作为误差收敛的条件。

2.2 迭代过程
(1)单动点弦截法:其中一个点相对固定,另一个点使用最新迭代点。
(2)双动点弦截法:每次迭代都使用最新的两个点作为弦的两个端点。
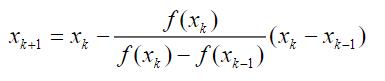
2.3 玄截法的优缺点
3. Python代码示例
(1)源代码
#导入库
from math import *
import time
import numpy
import matplotlib.pyplot as plt
# 一元N次非线性函数
# y=f(x) = x^3 - x - 1
def f(x):
return(1.0*x**3 - 1.0*x**1 -1) #原函数
#定义精度
accuracy = 0.0001
#定义初始弦点
#(-2, 2); (2, -2), (4,6), (-2, 0)
x0 = -2
x1 = 2
#log data
count = 0
x_data = []
y_data = []
#记录初始节点
x_data.append(0)
y_data.append(x1)
#迭代起始时间
start = time.time()
while True:
#新的一轮迭代
#x2 = x1 - (f(x1)/(f(x1) - f(x0))* (x1-x0)
x2 = x1 - (f(x1)/(f(x1)-f(x0))) * (x1-x0)
#迭代后误差
Err = fabs(x2-x1)
#迭代后,更新弦的两个端点
x0=x1
x1=x2
#增加log记录
count = count + 1
x_data.append(count)
y_data.append(x2)
if (Err <= accuracy):
break;
#迭代终止时间
end = time.time()
print("耗时=", end-start)
print("迭代次数=", count)
print("方程解=", x2)
print("实际误差=", Err)
print("\\n迭代过程")
for x in x_data:
print("X{}={}".format(x,y_data[x]))
plt.scatter(x_data, y_data)(2)输出结果
耗时= 0.0
迭代次数= 14
方程解= 1.3247179475513264
实际误差= 1.1443981175807139e-05
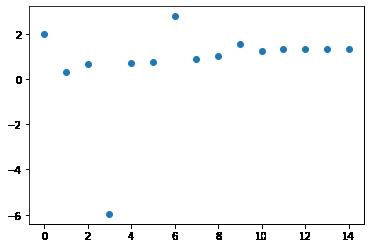
迭代过程
X0=2
X1=0.33333333333333326
X2=0.6764705882352942
X3=-5.9659037832788435
X4=0.7205447258552375
X5=0.7642428766142935
X6=2.7795773998506097
X7=0.9039311563739425
X8=1.0198194558275189
X9=1.5589937858809622
X10=1.2560469915663113
X11=1.3113074866299563
X12=1.3256266858160797
X13=1.3247065035701506
X14=1.3247179475513264(3)图形显示收敛过程
(4)不同初值值的迭代结果
- (-2, 2)

- (2, -2)

- (4, 6)
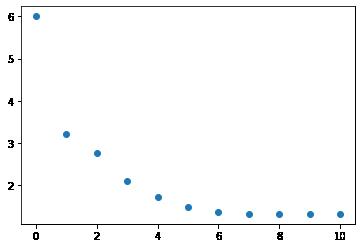
- (-2, 0 )

作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119821256

以上是关于[数值计算-8]:一元n次非线性方程求解-双点区间-弦截迭代法&Python法代码示例的主要内容,如果未能解决你的问题,请参考以下文章