[数值计算-9]：一元非线性函数求导数（数值微分）- 解析法与迭代法&Python法代码示例

Posted 2021-09-07 文火冰糖的硅基工坊

作者主页(文火冰糖的硅基工坊)：https://blog.csdn.net/HiWangWenBing

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/119824982

---

目录

1. 一元n次非线性方程

1.1 非线性函数

1.2 非线性函数案例

1.3 非线性函数的几何图形

2.  导数与解析法求导数

2.1 导数的源头和初心

2.2 什么导数

2.3 导函数

2.4 解析法求导数

3. 迭代法求导数的基本原理

3.1 数值微分的基本思想

3.2 确定误差或收敛条件：对导数值求误差

3.3 迭代过程: 对h进行迭代

4. Python代码示例

4.1 案例1：迭代法求导数

4.2 案例2：通过迭代法求导，获取导数序列

---

---

1. 一元n次非线性方程

1.1 非线性函数

线性函数是一次函数的别称，则非线性函数即函数图像不是一条直线的函数。

非线性函数包括指数函数、幂函数、对数函数、多项式函数等等基本初等函数以及他们组成的复合函数

1.2 非线性函数案例

 y = f(x) = a3*x^3 + a2*x^2 +  a0 

另a3 = 1， a2=-1， a0=-1；得到:

 

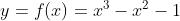
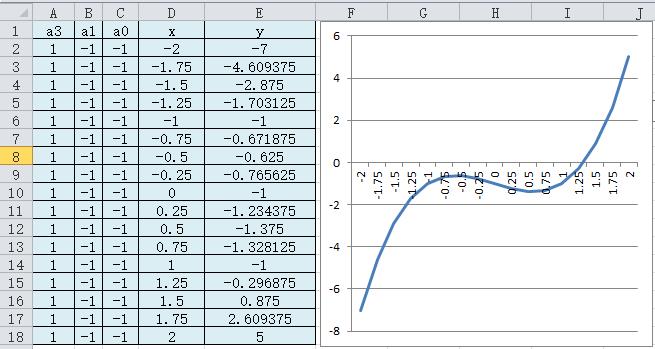
1.3 非线性函数的几何图形

2.  导数与解析法求导数

2.1 导数的源头和初心

在现实中，经常需要求函数的最大值、最小值、变速运动的瞬时速度，函数的切线等问题，是导数发现的源头与初心。

（1）瞬时速度

（2）切线与斜率

 

 

 

（3）函数求极值

 

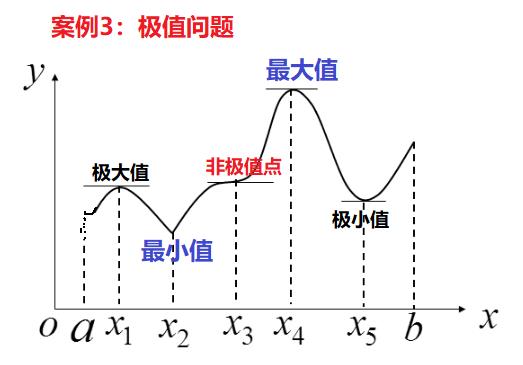
上述三个问题的本质，都与一个非常基础的概念相关，就是函数的导数！！！

 导数也是深度学习领域，求损失函数最小值中的一个基础性的概念，梯度下降法的基础就是导数。

2.2 什么导数

 导数也称为微分！！！

2.3 导函数

以x为自变量，以函数f(x)在x处的导数值为因变量y，而构成的函数为x的导函数，记成f'(x)。

实际上，大多数初等函数，都可以通过原函数f(x）直接获取f(x)的导函数。

有了导函数f'(x)，就可以直接求y=f(x)在任意点处的导数。

2.4 解析法求导数

解析法求导数，就是就是利用原函数，先人工得到导函数，然后，通过公式求解直接求解导数。

#导入库
from math import *
import time
import numpy as np
import matplotlib.pyplot as plt


# 一元N次非线性函数
# y=f(x) = x^3 - x - 1
def f(x):
    return(1.0*x**3 - 1.0*x**1 - 1) 

# 导函数：y=fv(x) =3x^2 - x
def fv(x):
    return(1.0*x**2 - 1.0*x**1 -1)  #导函数 


x_data = np.arange(-5,5,0.2)
y_data = []
print(x_data)

for x in x_data:
    y_data.append(fv(x))  #解析法依次求解
plt.scatter(x_data, y_data)

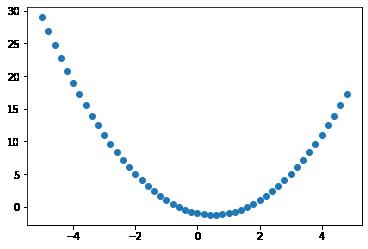
3. 迭代法求导数的基本原理

3.1 数值微分的基本思想

 

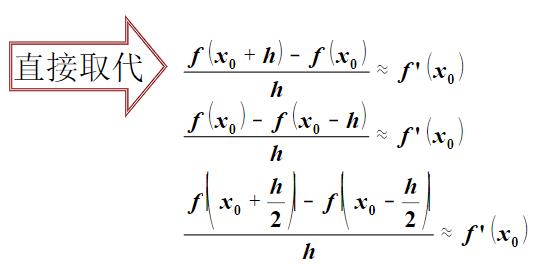
说明：x0 = a， x值为常量。

3.2 确定误差或收敛条件：对导数值求误差

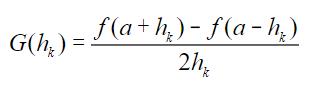
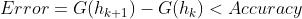
3.3 迭代过程: 对h进行迭代

 

 

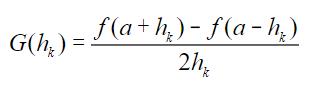
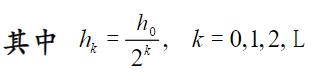
 也就是说，迭代的是离X0的距离h，距离逐渐减少，趋于无穷小时，按照上述的公式计算得到的就是此处的导数。

距离减少的规则采用的是指数下降法，也就是说迭代的方式指数下降迭代，而不是线性下降。

这种方式在精度和速度两个方面获得很好的平衡。

4. Python代码示例

4.1 案例1：迭代法求导数

（1）源代码：

#导入库
from math import *
import time
import numpy
import matplotlib.pyplot as plt

# 一元N次非线性函数
# y=f(x) = x^3 - x - 1
def f(x):
    return(1.0*x**3 - 1.0*x**1 - 1) 


# 导函数：y=fv(x) =3x^2 - 1
def fv(x):
    return(3.0*x**2 - 1.0)  #导函数 

# 定义通过迭代法求导数的函数
# X0: 需要求导的位置
# accuracy： 精度
# debug： 调试开关
def f_iter(X0, accuracy = 0, debug = 0):
    #log data
    k = 0
    x_data  = []
    y_data  = []
    z_data  = []
    
    if (debug!=0):
        print("\\n输入参数：X0={} , accuracy={}, debug={}".format(X0, accuracy, debug))
    #计算初始导数
    H0 = 1
    Hk = H0
    Gk = (f(X0 + Hk) - f(X0 - Hk))/(2*Hk)
    
    if (debug!=0):
        x_data.append(0)
        y_data.append(Gk)
        z_data.append(Hk)
    
    #迭代求导
    while True:
        k = k + 1  #记录迭代次数
        Hk = Hk/2                              #逐步逼近
        Gk_1 = Gk
        Gk = (f(X0 + Hk) - f(X0 - Hk))/(2*Hk) #导数值迭代
        Err = fabs(Gk - Gk_1)                 #求误差
        
        if (debug !=0):
            x_data.append(k)
            y_data.append(Gk)  
            z_data.append(Err)
        
        if (Err <= accuracy):
            break; 
            
    if (debug!=0):
        for x in x_data:
            print(x, y_data[x], z_data[x])
        print("\\n迭代图示")
        plt.scatter(x_data, y_data)
    return Gk

accuracy = 0.00001

a = 2

print("解析法求导：", fv(a))
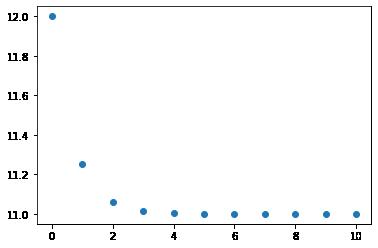
print("迭代法求导：", f_iter(a, accuracy, 1))

（2）输出结果

解析法求导： 11.0

输入参数：X0=2 , accuracy=1e-05, debug=1
0 12.0 1
1 11.25 0.75
2 11.0625 0.1875
3 11.015625 0.046875
4 11.00390625 0.01171875
5 11.0009765625 0.0029296875
6 11.000244140625 0.000732421875
7 11.00006103515625 0.00018310546875
8 11.000015258789062 4.57763671875e-05
9 11.000003814697266 1.1444091796875e-05
10 11.000000953674316 2.86102294921875e-06

迭代图示
迭代法求导： 11.000000953674316

（3）图形显示收敛过程

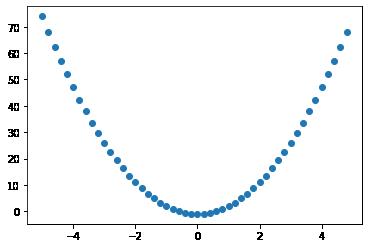
4.2 案例2：通过迭代法求导，获取导数序列

（1）源代码

# 定义存放导数序列的列表
x_data = np.arange(-5,5,0.2)
y_data = []

for x in x_data:
    #迭代法依次求导数
    y_data.append(f_iter(x, 0.0001, debug=0))   

# 展示导数序列
plt.scatter(x_data, y_data)

（2）图示输出（导函数）

---

作者主页(文火冰糖的硅基工坊)：https://blog.csdn.net/HiWangWenBing

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/119824982