超详细多元线性回归模型statsmodels_ols
Posted 土味儿大谢
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了超详细多元线性回归模型statsmodels_ols相关的知识,希望对你有一定的参考价值。
多元线性模型的主要作用:(主要进行预测)
通过建模来拟合我们所提供的或是收集到的这些因变量和自变量的数据,收集到的数据拟合之后来进行参数估计。参数估计的目的主要是来估计出模型的偏回归系数的值。估计出来之后就可以再去收集新的自变量的数据去进行预测,也称为样本量

import pandas as pd
import numpy as np
import statsmodels.api as sm#实现了类似于二元中的统计模型,比如ols普通最小二乘法
import statsmodels.stats.api as sms#实现了统计工具,比如t检验、F检验...
import statsmodels.formula.api as smf
import scipy
np.random.seed(991)#随机数种子
x1 = np.random.normal(0,0.4,100)#生成符合正态分布的随机数(均值,标准差,所生成随机数的个数)
x2 = np.random.normal(0,0.6,100)
x3 = np.random.normal(0,0.2,100)
eps = np.random.normal(0,0.05,100)#生成噪声数据,保证后面模拟所生成的因变量的数据比较接近实际的环境
X = np.c_[x1,x2,x3]#调用c_函数来生成自变量的数据的矩阵,按照列进行生成的;100×3的矩阵
beta = [0.1,0.2,0.7]#生成模拟数据时候的系数的值
y = np.dot(X,beta) + eps#点积+噪声
X_model = sm.add_constant(X)#add_constant给矩阵加上一列常量1,主要目的:便于估计多元线性回归模型的截距,也是便于后面进行参数估计时的计算
model = sm.OLS(y,X_model)#调用OLS普通最小二乘
results = model.fit()#fit拟合,主要功能就是进行参数估计,参数估计的主要目的是估计出回归系数,根据参数估计结果来计算统计量,这些统计量主要的目的就是对我们模型的有效性或是显著性水平来进行验证
results.summary()#summary方法主要是为了显示拟合的结果

一、回归系数的参数估计
1.1 最小二乘法实现参数估计——估计自变量X的系数

'''
回归系数的计算:X转置乘以X,对点积求逆后,再点乘X转置,最后点乘y
'''
beta_hat = np.dot(np.dot(np.linalg.inv(np.dot(X_model.T,X_model)),X_model.T),y)#回归系数
print('回归系数:',np.round(beta_hat,4))#四舍五入取小数点后4位
print('回归方程:Y_hat=%0.4f+%0.4f*X1+%0.4f*X2+%0.4f*X3' % (beta_hat[0],beta_hat[1],beta_hat[2],beta_hat[3]))

1.2 决定系数:R²与调整后R²
主要作用:检验回归模型的显著性
#因变量的回归值=np.dot(X_model,系数向量)
y_hat = np.dot(X_model,beta_hat)#回归值(拟合值)的计算
y_mean = np.mean(y)#求因变量的平均值
sst = sum((y-y_mean)**2)#总平方和:即y减去y均值后差的平方和
ssr = sum((y_hat-y_mean)**2)#回归平方和:y回归值减去y均值后差的平方和
#sse = sum((y-y_hat)**2)#残差平方和:y值减去y回归值之差的平方和
sse = sum(results.resid**2)#结果和上面注释了的式子一样,或许有小数点的误差,但基本上可忽略不计
R_squared =1 - sse/sst#R²:1减去残差平方和除以总平方和商的差;求解方法二:R²=ssr/sst
#按照线性回归模型原理来说:[残差平方和+回归平方和=总平方和]→[R²=ssr/sst]
print('R方:',round(R_squared,3))
#调整后平方和:100表示样本数据总数(n),3表示自变量个数(p)
adjR_squared =1- (sse/(100-3-1))/(sst/(100-1))#1-(残差的平方和/残差的自由度)/(总平方和/无偏估计)
#残差的自由度也是残差方差的无偏估计
print('调整后R方:',round(adjR_squared,3))

0≤R²≤1
R²>8说明模型显著性强
6<R²≤8说明模型还行
R²<6说明显著性不行了
1.3 F检验

F = (ssr/3)/(sse/(100-3-1));
print('F统计量:',round(F,1))
#累积分布函数叫cdf(),调用方法和下面残差函数调用方法一样;注意:cdf+sf算出来的值为1
F_p = scipy.stats.f.sf(F,3,96)#使用F分布的残存函数计算P值;sf是残存函数英语单词的缩写;3和96分别是两个自由度
print('F统计量的P值:', F_p)

1.4 对数似然、AIC与BIC
#对数似然值计算公式: L=-(n/2)*ln(2*pi)-(n/2)*ln(sse/n)-n/2;sse/n就是方差
res = results.resid#残差
#res = y-y_hat
sigma_res = np.std(res) #残差标准差
var_res = np.var(res) #残差方差
ll = -(100/2)*np.log(2*np.pi)-(100/2)*np.log(var_res)-100/2
print('对数似然:', round(ll,2))#保留两位小数
#赤池信息准则:-2乘以对数似然比+2*(参数个数+1)。
#−2ln(L)+2(p+1)(赤池弘次),其中p为参数个数,ln(L)即ll
AIC = -2*ll + 2*(3+1)
print('AIC:',round(AIC,1))
# 贝叶斯信息准则:−2ln(L)+ln(n)∗(p+1),其中ln(L)即llr
BIC = -2*ll+np.log(100)*(3+1)
print('BIC:',round(BIC,1))

1.5 回归系数标准差

from scipy.stats import t,f
C = np.linalg.inv(np.dot(X_model.T,X_model))#X倒置点乘X,然后对点集求逆
C_diag = np.diag(C)#取出C矩阵对角线的值
sigma_unb= (sse/(100-3-1))**(1/2)#残差标准差的无偏估计:残差平方和/(样本数减参数个数减1)
'''
回归系数标准差std err的计算:
计算方式:残差标准差(无偏估计)乘以(C矩阵对角线上对应值的平方根)
'''
stdderr_const = sigma_unb*(C_diag[0]**(1/2))#常数项(截距)的标准差,对应C_diag[0]
print('常数项(截距)的标准差:',round(stdderr_const,3))
stderr_x1 = sigma_unb*(C_diag[1]**(1/2))#第一个系数对应C_diag[1]
print('beta1的标准差:',round(stderr_x1,3))
stderr_x2 = sigma_unb*(C_diag[2]**(1/2))#第二个系数对应C_diag[2]
print('beta2的标准差:',round(stderr_x2,3))
stderr_x3 = sigma_unb*(C_diag[3]**(1/2))#第三个系数对应C_diag[3]
print('beta3的标准差:',round(stderr_x3,3))

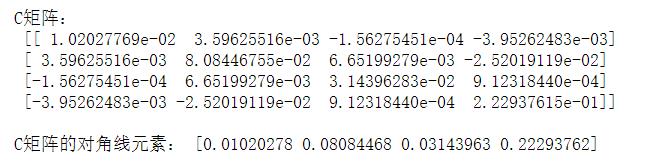
print('C矩阵:\\n', C)
print('\\nC矩阵的对角线元素:',C_diag)
1.6 回归系数的显著性检验(t检验)

t值足够小就可以认为回归方程的系数是具有显著性的,显著性水平是比较高的,否则就可以认为这个回归系数的显著性不高
'''
回归方程的显著性检验
(1) t检验:beta_hat[i](相应的回归系数)除以相应系数标准差
(2) 使用scipy.stats.t.sf残存函数(Survival function),
等于:1-累积分布函数(1-cdf);
由于是对t的绝对值进行检验,因此需要乘以2。即p<-t与p>t之和
'''
t_const = beta_hat[0]/stdderr_const
print('截距项的t值:',round(t_const,3))
p_const = 2*t.sf(t_const,96)
print("P>|t|:",round(p_const,3))
t_x1 = beta_hat[1]/stderr_x1
print('x1系数的t值:',round(t_x1,3))
p_t1 = 2*t.sf(t_x1,96)
print("P>|t|:",round(p_t1,3))
t_x2 = beta_hat[2]/stderr_x2
print('x2系数的t值:',round(t_x2,3))
p_t2 = 2*t.sf(t_x2,96)
print("P>|t|:",round(p_t2,3))
t_x3 = beta_hat[3]/stderr_x3
print('x3系数的t值:',round(t_x3,3))
p_t3 = 2*t.sf(t_x3,96)
print("P>|t|:",round(p_t3,3))

p值>0.05就说明显著性很低,上图截距项的p值=0.329远大于0.05,所以不能拒绝原假设,也就是可以去掉截距项
1.7 回归系数的置信区间

'''
回归系数置信区间计算公式:
betahat_i - t.ppf(1-alpha/2,n-p-1)*sigma_unb*C_diag[0]**(1/2)
< =beta_i <=
betahat_i + t.ppf(1-alpha/2,n-p-1)*sigma_unb*C_diag[0]**(1/2)
t(1-alpha/2,n-p-1)是t值在0.025,自由度为n-p的分位数,由于下分位数是负值,
所以这里使用0.975来计算分位数的。调用scipy.stats.t.ppf进行计算,
实际就是cdf函数的逆函数,计算的是百分位数。
ppf和cpf的区别:ppf其实就是通过概率来求随机变量的值;cdf是通过随机变量的值来求概率的
sigma_unb*C_diag[0]**(1/2)就是前面计算系数标准差的公式,这里可以直接用
系数标准差代替。
特别要注意:要使用残差标准差的无偏估计,即sigma_unb。
ppf是percent point function的简称,用来计算百分位数。
根据置信区间的理论,t分布的概率密度函数关于y轴对称,其均值为0
其显著性水平为alpha(置信度为1-alpha)的概率分布函数的分位数,一般通过1-alpha/2进行计算
'''
const_inter_left = beta_hat[0] - t.ppf(0.975,96)*sigma_unb*C_diag[0]**(1/2)#置信下限
const_inter_right = beta_hat[0] + t.ppf(0.975,96)*sigma_unb*C_diag[0]**(1/2)#置信上限
print('常数项的置信区间是: [%0.3f,%0.3f]'%(const_inter_left,const_inter_right))
beta1_inter_left = beta_hat[1] - t.ppf(0.975,96)*sigma_unb*C_diag[1]**(1/2)
beta1_inter_right = beta_hat[1] + t.ppf(0.975,96)*sigma_unb*C_diag[1]**(1/2)
print('x1系数的置信区间是: [%0.3f,%0.3f]'%(beta1_inter_left,beta1_inter_right))
beta2_inter_left = beta_hat[2] - t.ppf(0.975,96)*sigma_unb*C_diag[2]**(1/2)
beta2_inter_right = beta_hat[2] + t.ppf(0.975,96)*sigma_unb*C_diag[2]**(1/2)
print('x2系数的置信区间是: [%0.3f,%0.3f]'%(beta2_inter_left,beta2_inter_right))
beta3_inter_left = beta_hat[3] - t.ppf(0.975,96)*sigma_unb*C_diag[3]**(1/2)
beta3_inter_right = beta_hat[3] + t.ppf(0.975,96)*sigma_unb*C_diag[3]**(1/2)
print('x3系数的置信区间是: [%0.3f,%0.3f]' % (beta3_inter_left,beta3_inter_right))

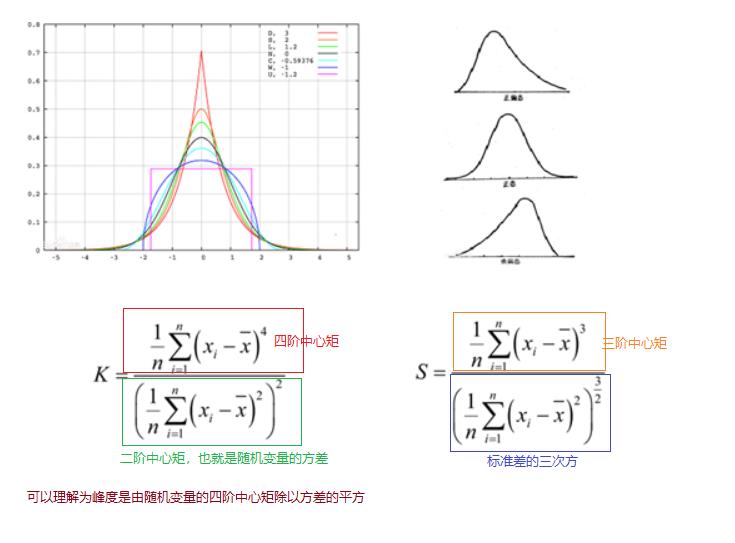
1.8 峰度与偏度
'''
1、注意峰度的定义方式有两种:一是Fisher定义,正态分布值为0;另一个是Pearson定义,正态分布值为3。
StatsModels使用的是Pearson定义。按照Fisher定义,逢峰度=0表示正好符合正正态分布,
大于0表示峰比较尖,反之表示比较平。
2、对于偏度,偏度值大于0则为正偏态或左偏态;小于零则表示负偏态或右偏态。
'''
#kurtosis = ((np.sum((res-res.mean())**4))/100)/((np.sum ((res-res.mean())**2)/100)**(1/2)-3 #Fisher定义峰度
#Pearson定义峰度
res_kurt = ((np.sum((res-res.mean())**4))/100)/((np.sum ((res-res.mean())**2)/100)**2)
res_skew = np.sum((res-res.mean())**3)/((sigma_res**3)*100)
#res_skew =
'''
#或者使用scipy的函数计算峰度和偏度
from scipy.stats import kurtosis,skew
res_kurt = kurtosis(res,fisher=False) #计算峰度,fisher=False表示按照pearson定义的方式计算峰度
res_skew = skew(res) #计算偏度
#也可以用pandas计算偏度和峰度,三种计算方式都有一定误差
import pandas as pd
resFrame = pd.Series(res)
res_kurt = resFrame.kurt()
res_skew = resFrame.skew()
'''
print('残差峰度(Pearson定义):',round(res_kurt,3))
print('残差偏度:',round(res_skew,3))
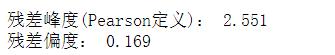
1.9 Jarque-Bera检验与Omnibus检验
1.9.1 Jarque-Bera检验
'''
#Jarque-Bera检验,使用scipy
from scipy.stats import jarque_bera
jb_test = jarque_bera(res)
'''
'''#使用statsmodels.stats.api进行Jarque-Bera检验
jb_test = sms.jarque_bera(res)#返回值是个命名元组,包含J_B值及其P值
'''
#全手动计算J_B值及其P值
from scipy.stats import chi2
#雅克贝拉值=样本量/6*(偏度²+峰度²/4)
jb_value = 100 / 6 * (res_skew**2 + (res_kurt - 3)**2 / 4)#-3是因为用的Fisher定义的峰度值,而不是皮尔逊定义的
jb_p = chi2.sf(jb_value, 2)#计算雅克贝拉检验其实就是计算雅克贝拉值的分布的残存函数的值,其中的2是卡方分布的自由度;卡方分布的自由度是与构成卡方分布的数据里面的参数个数有关。上式使用的是两个参数:偏度和峰度,因此这里自由度是2
print('Jarque-Bera (JB): ',round(jb_value,3))
print('Prob(JB): ',round(jb_p,3))

1.9.2 Omnibus检验
#omnibus检验,使用statsmodels
omnibus_test = sms.omni_normtest(res) #omnibus检验
print('Omnibus:',round(omnibus_test.statistic,3))#omnibus的统计量
print('Prob(Omnibus): ',round(omnibus_test.pvalue,3))#omnibus的p值
'''
Omnibus检验的具体步骤:
(1)计算残差的偏度检验值和峰度检验值。
(2)求出二者平方和。
(3)以平方和和自由度2为参数调用卡方分布的残存函数。
(4)平方和是Omnibus统计量的值,残存函数返回值是Omnibus统计量的P值。
从此示例可以看出scipy科学与统计计算功能之强大!
'''
from scipy.stats import normaltest,skewtest,kurtosistest,skew,kurtosis,chi2
#normaltest(res)#此函数直接进行Omnibus检验
s, _ = skewtest(res)#注意:偏度检验和偏度并不是一回事
k, _ = kurtosistest(res)#峰度检验和峰度也不是一回事
k2 = s*s + k*k
print('------------------手动计算Omnibus检验----------------------')
print('Omnibus: ', np.round(k2,3))#
print('Prob(Omnibus):', np.round(chi2.sf(k2,2),3))#通过卡方分布的残存函数计算Omnibus的P值。

1.10 Dubin-Watson检验
'''
Durbin-Watson检验:越接近2,表示残差越接近正态分布
#直接调用sms.durbin_watson()函数
dw = sms.durbin_watson(res)
'''
#原始计算公式:残差的差值平方和除以残差平方和
diff_resids = np.diff(res)
dw = np.sum(diff_resids**2) / np.sum(res**2)
print('Durbin-Watson: ',round(dw,3))

1.11 条件数Cond. No.
900以内为佳
'''
条件数(Cond. No.)的计算步骤如下:
(1)获取增加常量1向量后的自变量矩阵,X_model
(2)计算X_model转置与其本身的点积C
(3)计算点积的特征值
(4)最大特征值/最小特征值,然后将结果开平方
条件数是衡量矩阵病态的一个指标,理论上该值越小越好。
'''
#C= np.dot(X_model.T,X_model)
eigs = np.linalg.eigh(C)[0] #linalg线性代数的缩写,eigh特征值单词的缩写。eig也可以计算特征值,主要可以计算一般的矩阵;eigh计算的矩阵是对称矩阵,计算出来的特征值会从小到大进行排序
cond = np.sqrt(eigs[-1]/eigs[0])#(最大特征值/最小特征值)²
print('通过特征值计算Cond. No.: ',round(cond,3))
'''
条件数的另一种计算法:sqrt(||C||*||inv(C)||),
即用矩阵C的范数乘以C逆的范数,然后再开平方。
'''
cond = np.sqrt(np.linalg.norm(C,ord=2)*np.linalg.norm(np.linalg.inv(C),ord以上是关于超详细多元线性回归模型statsmodels_ols的主要内容,如果未能解决你的问题,请参考以下文章