岭回归与lasso回归算法
Posted 土味儿大谢
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了岭回归与lasso回归算法相关的知识,希望对你有一定的参考价值。
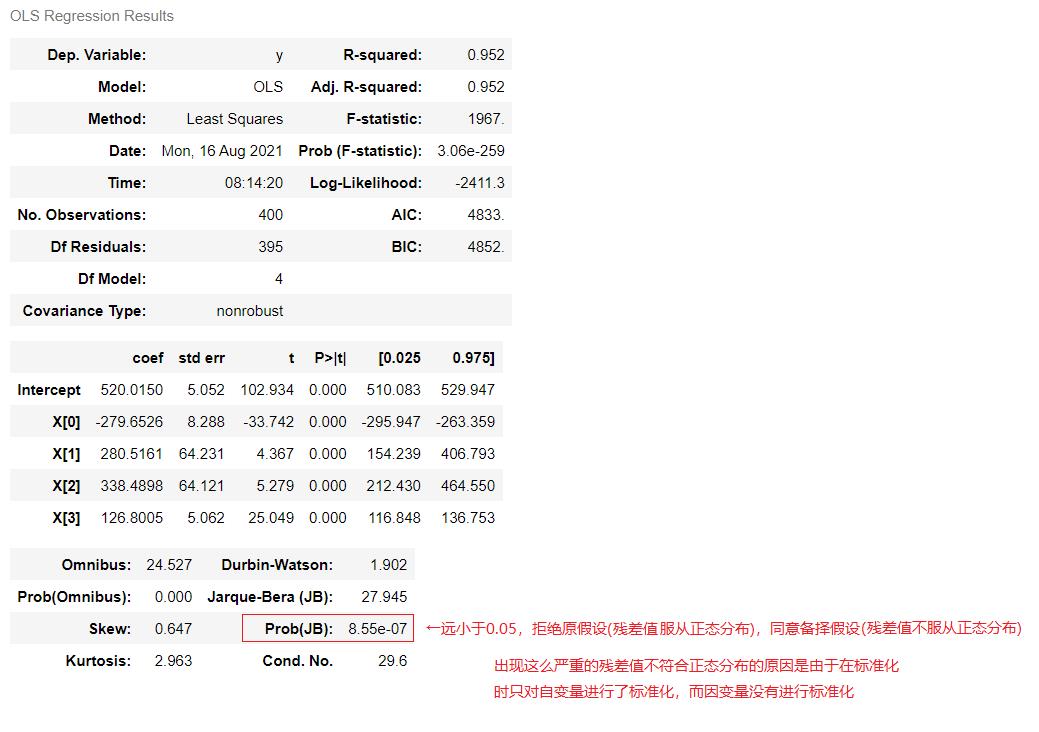
模型压缩与正则化主要包含岭回归(Ridge regression)和Lasso两种方法,二者的主要原理是将系数往等于0的方向压缩。
岭回归
lasso
全称:Least absolute shrinkage and selection operator最小绝对缩减和选择算子
一、岭回归示例
使用信用卡数据进行岭回归。
信用卡数据字段:
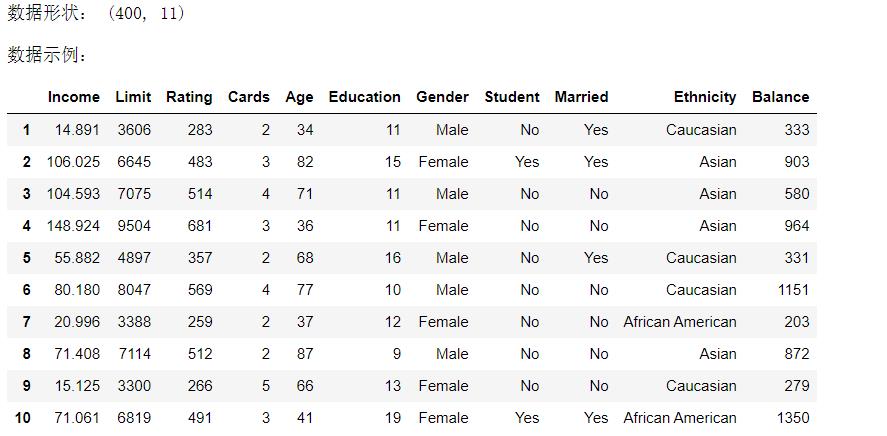
Income:收入,Limit:信用额度,Rating:信用等级,Cards:信用卡数, Age:年龄, Education:教育程度 ,Gender:性别,Student:是否学生,Married:是否已婚,Ethnicity:种族,Balance:余额
from sklearn.preprocessing import StandardScaler #进行标准化需要用
import statsmodels.formula.api as smf #公式化回归分析的模型
import seaborn as sns #画图用
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import patsy
data = pd.read_csv(r'e:\\data\\credit.csv',index_col=0)
print('数据形状:',data.shape)
print('\\n数据示例:')
data.head(10)
'''
使用Income,Limit,Rating,Student四个属性作为自变量,使用Balance做因变量
构建模型,即通过收入,信用额度,信用等级和是否学生来预测余额。
对于超参数lambda,设定从10^(-2)到10^10次方超参数集等距挑选100个数进行测试。
'''
X = data[['Income','Limit','Rating','Student']] #自变量
y = data['Balance'] #因变量
###将因子变量映射成0,1
X['Student'] = X['Student'].map({'Yes':1,'No':0})
###对数字变量进行标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
formula = 'y~X'
model=smf.ols(formula,data={'y':y,'X':X_scaled})
result=model.fit()
result.summary()
mse = []###残差均方
###超参数的范围,100个,从10^-2到10^10
lam=10**np.linspace(-5,10,100)#返回list对象,10^-5到10^10按照等间隔来获取100个数值
###Statsmodels有一个岭回归和Lasso的简单实现即fit_regularized函数
for l in lam:
###L1_wt:0为岭回归;1为Lasso;0-1之间为ElasticNet算法(也就是所谓的弹性网络);alpha也就是λ;refit是否要进行重新拟合;profile_scale是否进行伸缩
result = model.fit_regularized(L1_wt=0,alpha=l,refit=True,profile_scale=False)
###使用原始数据进行预测
pred=result.predict()
###计算残差均方(均方误差)
mse.append(np.sum(y-pred)**2)
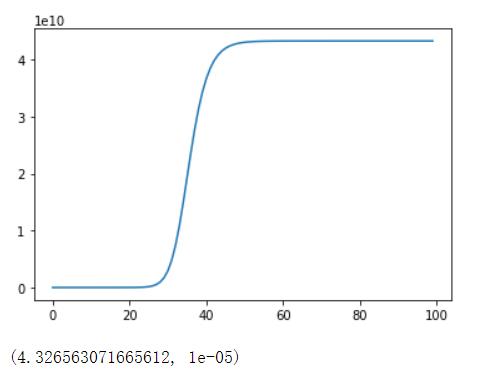
sns.lineplot(np.arange(0,len(mse)),mse)
plt.show()
lammin=lam[np.argmin(mse)]#取出残差值中最小的那个均方误差
###最小均方残差以及lambda超参数的值
np.min(mse),lammin
'''
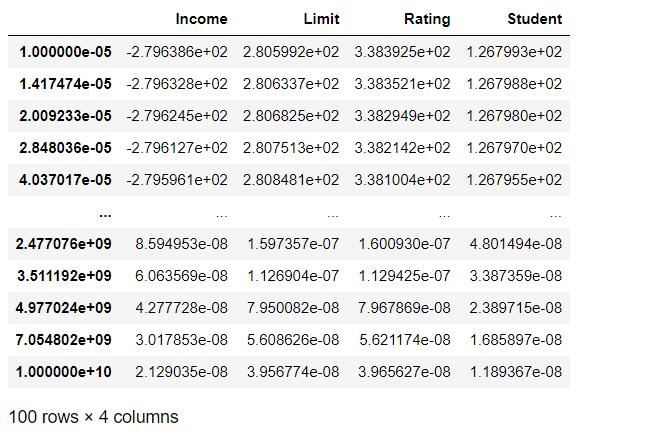
岭回归随着lambda->Inf,压缩惩罚项影响力增加,岭回归系数估计值越接近0.
见下图。
'''
##超参数lambda,有的教材也用alpha
# 设置matplotlib参数,正确显示中文和'-'符号。
plt.rcParams.update(
{
'text.usetex': False,
'font.family': 'stixgeneral',
'mathtext.fontset': 'stix',
}
)
alpha=10**np.linspace(-5,10,100)
intercept_dict = {}#回归系数保存在这里
for a in alpha:
result = model.fit_regularized(L1_wt=0,alpha=a,refit=True,profile_scale=True)
###保存每次迭代的回归系数估计值
intercept_dict[a]=result.params
###lambda参数与对应的系数估计值,去掉截距项
params_l2 = pd.DataFrame(intercept_dict).T #一定要转置
params_l2=params_l2[[1,2,3,4]]
###行索引是alpha值,列索引是自变量名
params_l2.columns=['Income','Limit','Rating','Student'] #取列名
plt.figure(figsize = (12,6)) #设置图像大小,宽12高6
###Seaborn使用行索引为X轴,每一列的数据为Y轴,绘制曲线
#列名作为示意图的标记。
sns.lineplot(data = params_l2,dashes=True)
plt.axhline(y = 0,linestyle = 'dashed',lw = 0.8,color = 'black') #绘制一条平行于x轴的直线方便观察回归系数曲线是否向0逼近
plt.xticks(alpha) #x轴的刻度值
###对X轴进行对数转换伸缩。
plt.xscale('log')#取x的对数值来变换,若不进行变换曲线就会很丑
plt.ylim(-300,400) #y轴的最小最大值
plt.xlim(10**(-3)-0.0001,10**3) #x轴的最小最大值
plt.ylabel('Coeffients',size=14) #标签
plt.xlabel('Alpha',size=14)
plt.show()

###不同lambda值下的回归系数,
#很显然,随着lambda值不断变大,系数向零缩减,非常接近于零。
params_l2
二、Lasso示例
相对于岭回归不做自变量的选择,lasso可以选择自变量,将不重要自变量的系数压缩至0。
因此称lasso模型为稀疏模型
'''
Lasso变量选择,某些自变量系数估计值压缩为零。
首先构建包含所有自变量的的模型,注意要对属性类型进行因子化,即转换成哑变量。
'''
#尽量使用深度拷贝data.copy()赋值给x,避免影响到原数据
X = data #引用赋值,对X操作会影响data的数据
scaler = StandardScaler()#标准化处理
X[['Income','Limit','Rating','Cards','Age','Education']]=scaler.fit_transform(
X[['Income','Limit','Rating','Cards','Age','Education']])
X['Balance']=data['Balance']
###模型包含了所有自变量,对于因子变量通过patsy的C函数转换成category类别变量,它返回的是dmatrix设计矩阵
formula = 'Balance~Income+Limit+Rating+Cards+Age+Education+C(Gender)\\
+C(Student)+C(Married)+C(Ethnicity)' #C()将属性变量进行因子化或是类别化形成相关的设计矩阵
model=smf.ols(formula,data=X) #普通回归模型
result_ols=model.fit() #调用普通最小二乘的fit()函数来进行计算
alpha=10**np.linspace(-2,4,100) #超参数 10^-2到10^4
###系数的绝对值之和
betaols_l1=np.sum(np.abs(result_ols.params)) #取出通过普通最小二乘模型拟合后所得到的参数的结果来取绝对值后再求和
params_l1 = {} #声明一个变量来保存每一次迭代之后参数的值
params2_l1 = {} #声明一个变量来保存特殊的值
for a in alpha:
result = model.fit_regularized(L1_wt=1,alpha=a)
params=result.params #取出每一次迭代后所生成的result的回归系数
params_l1[a]=params #取出来后通过alpha来作为字典的键,以parmas作为值
rate=np.sum(np.abs(params))/betaols_l1 #绘制压缩图(正则化路径图)时候用;所谓正则化路径图就是:哪些自变量的回归系数是在什么时候通过什么样的路径进入到模型里的,反过来讲就是这些自变量的系数是按照哪一种顺序先后被压缩到这个模型里的
###保存每个alpha参数回归之后的系数与未正则化模型的系数
#的l1范数之比作为字典的键,以系数作作为值
#用于下个代码单元绘制正则化路径图。
params2_l1[rate] = params #以rate作为键,parmas作为值
###lambda参数与对应的系数估计值,去掉截距项
params_l1 = pd.DataFrame(params_l1).T #同理也要转置
params2_l1 = pd.DataFrame(params2_l1).T
del params_l1['Intercept'] #去掉截距项
del params2_l1['Intercept']
plt.figure(figsize = (10,6))
sns.lineplot(data = params_l1,dashes=False) #dashes=False避免报错
plt.axhline(y = 0,lw = 0.1,color = 'black') #参考线
plt.xticks(alpha,fontsize=14)
plt.yticks(fontsize=14)
plt.xscale('log')
plt.ylabel('Coeffients',size=14)
plt.xlabel('Alpha',size=14)
# 示意图:根据不同颜色的曲线对应不同系数的名称
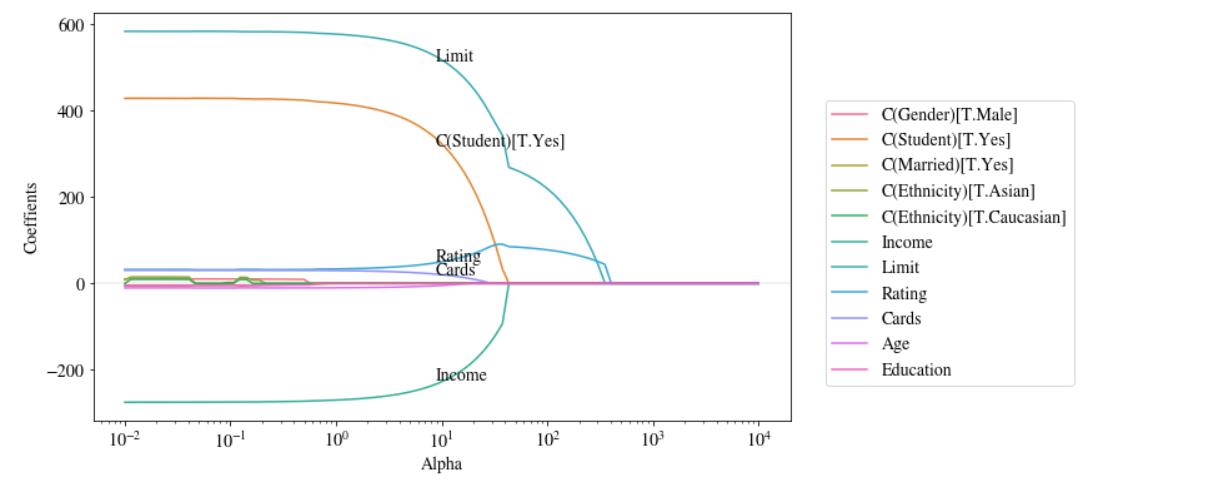
plt.legend(bbox_to_anchor=(1, 0), loc=3, borderaxespad=2,fontsize=14) #设置示意图所在位置,loc=3就是设置在图形外面;borderaxespad边界
###在曲线上标注系数名(只标注值大于10的系数)
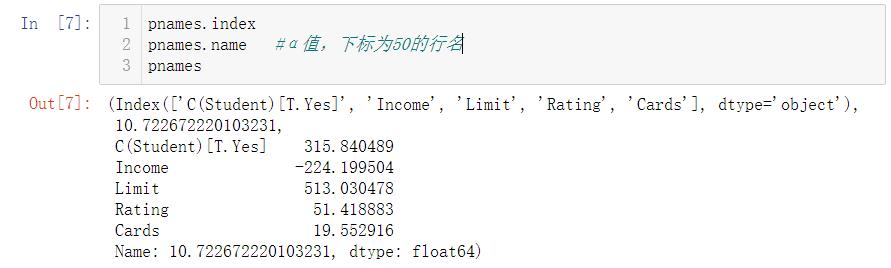
pnames=params_l1.iloc[50].iloc[np.where(np.abs(params_l1.iloc[50])>10)]
xn=pnames.name #α值,行名
for p in pnames.index:
yn=pnames.loc[p] #列名所对应的值
plt.text(xn-2,yn,p,fontsize=14) #xn-2往左距离2个刻度;p是列名
plt.show()

'''
下图可以看出变量进入模型的先后顺序-即所谓“正则化路径(regularization path)”
先后进入模型的变量依次是:Rating,Limit、Student和Income
'''
plt.figure(figsize = (10,6))
sns.lineplot(data = params2_l1,dashes=False)
plt.axhline(y = 0,lw = 0.1,color = 'black')
plt.xticks(alpha) #x轴的刻度
plt.xscale('log')
plt.ylabel('Coeffients',fontsize=14)
plt.xlabel('|beta_i|/|beta_ls|',fontsize=14)
plt.legend(bbox_to_anchor=(1, 0), loc=3, borderaxespad=2,fontsize=14)
###在曲线上标注系数名(注:此处只标注值绝对值大于5的系数),在第59个数据处进行标注
pnames=params2_l1.iloc[59].iloc[np.where(np.abs(params2_l1.iloc[59])>5)]
xn=pnames.name##lambda的值
for p in pnames.index:
yn=pnames.loc[p]
plt.text(xn-0.1,yn,p,fontsize=14)
plt.xticks(size=14)
plt.show()

三、正则化与变量选择
### 岭回归的模型正则化
#alpha=1000时,系数被缩减到0附近
result_test1 = model.fit_regularized(L1_wt=0,alpha=1000)
result_l2=result_test1.params
result_l2

### Lasso的变量选择
#设置alpha=4,很多系数被缩减为0
result_test = model.fit_regularized(L1_wt=1,alpha=20)
result_l1=result_test.params
result_l1

四、最优 𝜆 参数选择
选择fit_regularized函数参数 𝛼 的最优值
X1=data.copy() #深度拷贝
#1、哑变量的构造
dummies1 = pd.get_dummies(X1.Student, prefix='Student') #get_dummies哑变量
dummies2 = pd.get_dummies(X1.Gender, prefix='Gender')
dummies3 = pd.get_dummies(X1.Married, prefix='Married')
dummies4 = pd.get_dummies(X1.Ethnicity, prefix='Ethnicity')
#2、删掉原数据,加入哑变量数据
X1=X1.drop('Student',axis=1).join(dummies1)
X1=X1.drop('Gender',axis=1).join(dummies2)
X1=X1.drop('Married',axis=1).join(dummies3)
X1=X1.drop('Ethnicity',axis=1).join(dummies4)
#3、删掉部分哑变量,避免产生多重共线性
X1=X1.drop('Student_No',axis=1)
X1=X1.drop('Gender_Female',axis=1)
X1=X1.drop('Married_No',axis=1)
X1=X1.drop('Ethnicity_African American',axis=1)
scaler = StandardScaler() #标准化数值数据
X1[['Income','Limit','Rating','Cards','Age','Education','Balance']]=scaler.fit_transform( \\
X1[['Income','Limit','Rating','Cards','Age','Education','Balance']])
#X1['Balance']=data['Balance']
dummies1,X1.head()

'''
岭回归最优lambda参数选择
'''
import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn.linear_model import Ridge,RidgeCV,LassoLarsIC #CV是交叉验证的意思
from sklearn.metrics import mean_squared_error #评价交叉验证的结果通过mean_squared_error(均方误差)评价
#拆分为训练集和测试集
predictors=['Income','Limit','Rating','Cards','Age','Education',
'Student_Yes','Gender_Male','Married_Yes',
'Ethnicity_Asian','Ethnicity_Caucasian'] #所有列名
#这四个变量分别为:自变量的训练集和测试集,因变量的训练集和测试集
x_train,x_test,y_train,y_test=model_selection.train_test_split(X1[predictors],
X1.Balance,test_size=0.2, #测试集占20%
random_state=1234)
#构造不同的lambda值
Lambdas=np.logspace(-10,10,200)
#设置交叉验证的参数,使用均方误差评估;均方误差越大说明模型效果越差,负均方误差则越大越好
ridge_cv=RidgeCV(alphas=Lambdas,normalize=True,scoring='neg_mean_squared_error',cv=10) #RidgeCV(超参数的取值范围,是否标准化,通过负均方误差打分,cv=10)
ridge_cv.fit(x_train,y_train) #以训练集对模型进行拟合,拟合的结果就是最佳的α值
#基于最佳lambda值建模
ridge=Ridge(alpha=ridge_cv.alpha_,normalize=True) #alpha_最佳的α值作为参数来调用Ridge;normalize=True:要进行标准化
ridge.fit(x_train,y_train) #拟合
#打印回归系数
print(pd.Series(index=['Intercept']+x_train.columns.tolist(),
data=[ridge.intercept_]+ridge.coef_.tolist())) #intercept_;截距项;coef_:岭回归的系数
#模型评估
ridge_pred=ridge.predict(x_test) #用测试数据进行预测
#均方误差
MSE=mean_squared_error(y_test,ridge_pred)
print('MSE:',MSE,'\\naplha:',ridge_cv.alpha_)

'''
Lasso的Lambda最优值选择。
使用sklearn相关函数,比如LassoCV等。
'''
import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn.linear_model import Lasso,LassoCV
from sklearn.metrics import mean_squared_error
predictors=['Income','Limit','Rating','Cards','Age','Education',
'Student_Yes','Gender_Male','Married_Yes',
'Ethnicity_Asian','Ethnicity_Caucasian']
x_train,x_test,y_train,y_test=model_selection.train_test_split(X1[predictors],
X1.Balance,test_size=0.2,
random_state=1234)
#构造不同的lambda值
Lambdas=np.logspace(-5,10,200)
#设置交叉验证的参数,使用均方误差评估
lasso_cv=LassoCV(alphas=Lambdas,normalize=False,cv=10,max_iter=10000)


