Datawhale8月组队学习之函数极限与连续性

Posted 2021-09-07 临风而眠

Datawhale8月组队学习之函数极限与连续性

​ 本来是因为报了全国大学生数学竞赛，想借此机会复习一下大一 一年已经忘掉的微积分，发现任务好多😢

​ 不过提前体验一下考研的毒打也还行吧555…😭，既然报了就坚持

一.preparation

课本：

《2022考研张宇考研数学基础30讲》 《2022考研数学张宇数学题源探析经典1000题(数学一)》

本期任务：

张宇数学(一) 1000题 第一章 ：函数极限与连续

强化训练

• 函数有界性：

• 选择题：1

• 函数渐近线：

  • 选择题：2

• 简答题：26

• 无穷小量与无穷大量：

  • 选择题：3、4、5、6、7、8、9、10、11、12、13
  • 简答题：29
  • 计算题：30:(1)、(2)、(3)

• 填空题：18、19、21、22

• 间断点、函数连续性：

  • 计算题：14、15、16；31、32、33、35；

• 填空题：17

• 求极限：

  • 填空题: 20、23、24、25
  • 简答题：27
  • 计算题: 28：(1)、(2)、(3)、(4)、(5)、(6)、(7)、(8)、(9)、(11)、(12)、(13)、(14)、(16)

巩固提高

• 无穷大量与无穷小量：

• 选择题：1、2；

• 函数连续性、间断点：

• 选择题：3、4、5；

• 求极限：

  • 解答题：7；
  • 计算题：8：(1)、(2)、(3)、(4)、(5)；

• 简答题：10；

• 渐近线问题：9、11；

​ 呜呜呜毕竟大一升大二的小朋友，我还是就挑一些练一练

二.高数学习脉络

​ 很粗略的思维导图

三.函数极限与连续基础知识

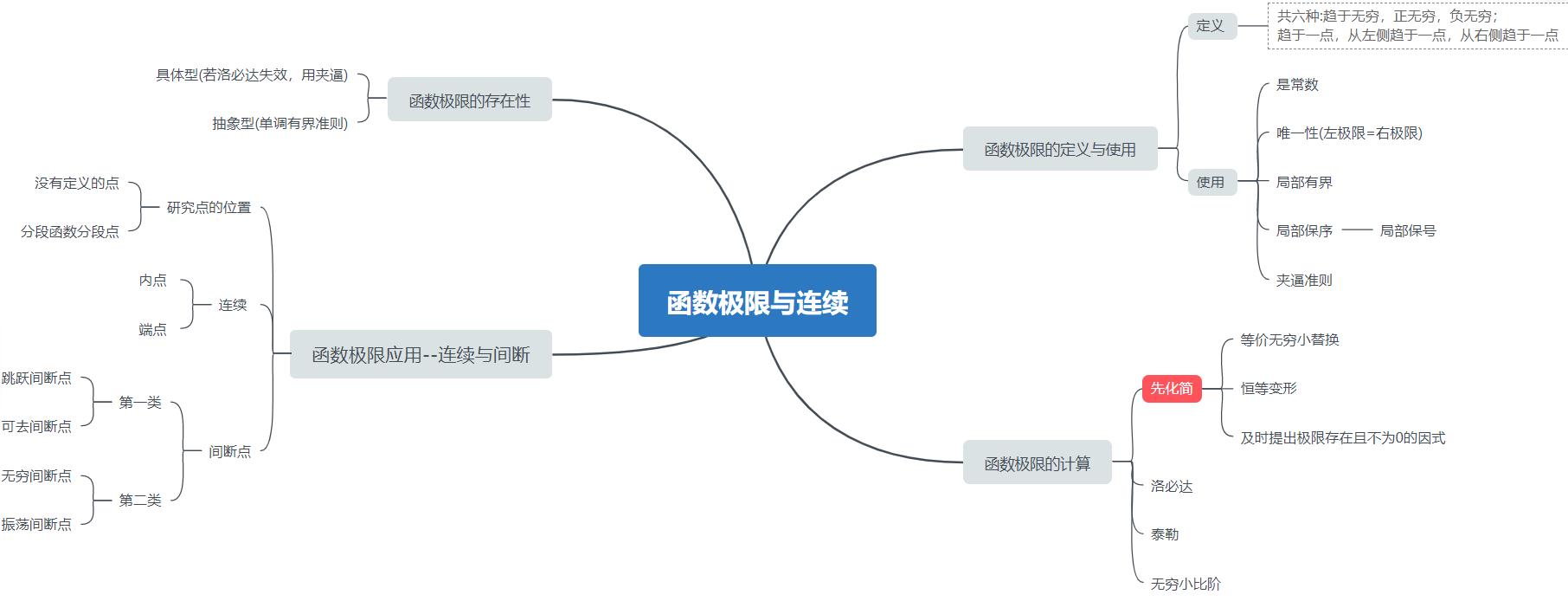
1.思维导图

2思维导图细节补充

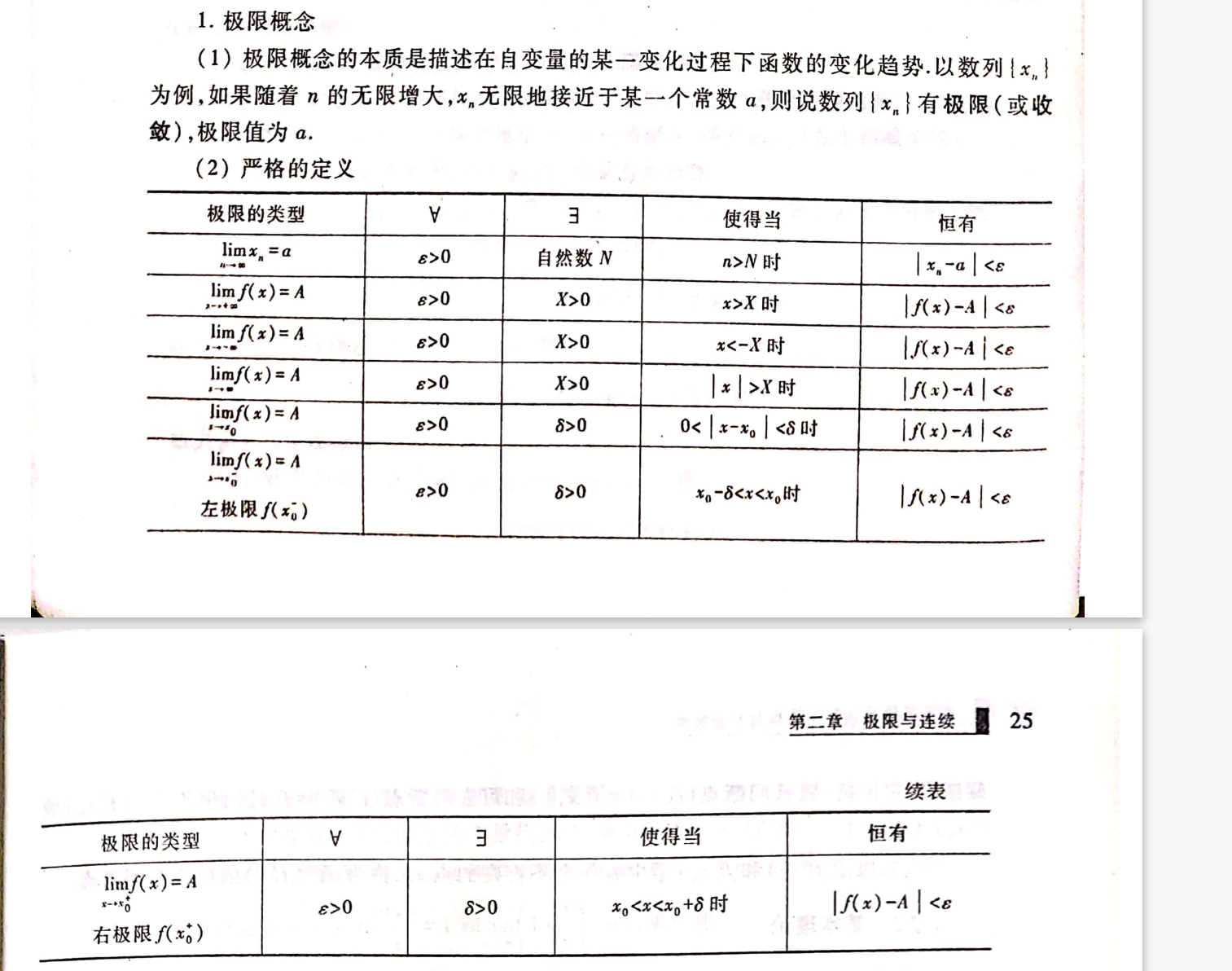
①函数极限定义

②函数极限的计算

针对7种未定式:

​ 通俗讲法：除了有限比有限的就是未定式

​ 计算之前先化简

• 换元

• 分子有理化

• 因式分解

• 幂指函数

  $u^v=e^{vlnu}$

Ⅰ.常用的等价无穷小

Ⅱ.Taylor

泰勒定理、泰勒中值定理

常用麦克劳林展开式

记忆技巧:

​ $sinx$是奇函数，分母都是奇数的阶乘

​ $cosx$是偶函数，分母都是偶数的阶乘

​ 其他的非奇非偶的，每一项都有

​

​ 结合级数去记：

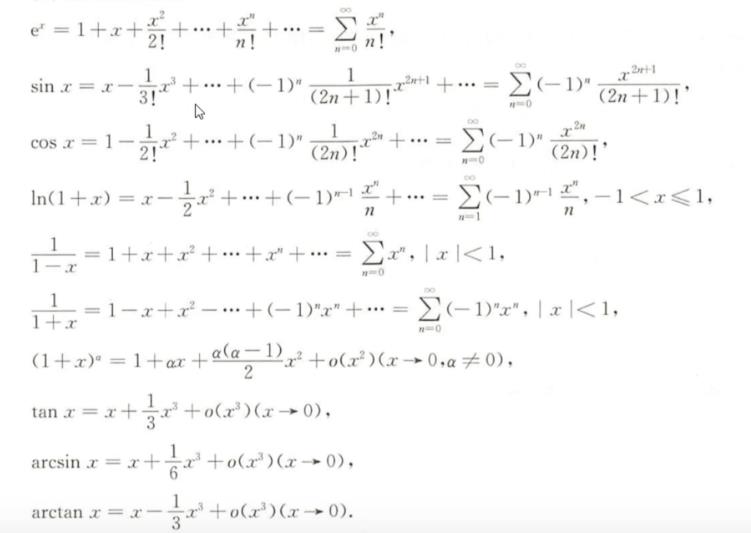
展开原则

• ​ $\frac{A}{B}$型,上下同阶

  展开后，分子分母要都展开到x的k次幂

• $A-B$型,幂次最低

  A、B分别展开到它们的系数不相等的x的最低次幂为止

Ⅲ.洛必达法则

​ 一定要说了可导才能用

Ⅳ.无穷小比阶

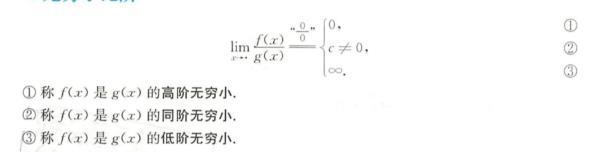
​ 其中若c=1，则为等价无穷小

​ 此题”抓大头“思想利用等价将$x^3\cos \frac{1}{x}$消掉了

③函数的连续性

Ⅰ.连续

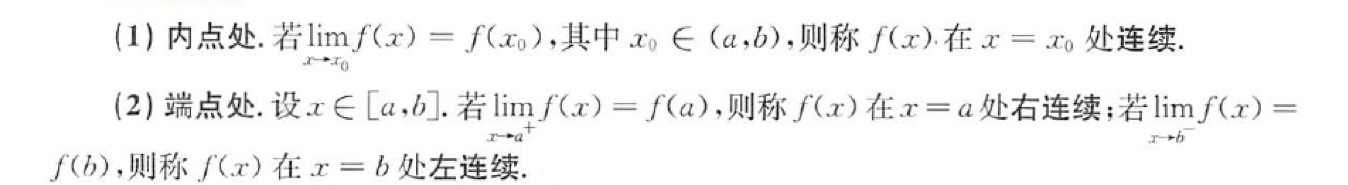
Ⅱ.间断

​ 以下前提：$f(x)$在$x=x_0$左右两侧均有定义

第一类

​ 第一类左右极限都存在

• 可去间断点

  

  ​ 只要修改或者补充$f(x_0)$,$f(x)$就会在$x_0$连续

• 跳跃间断点

  $x_0$的左右极限均存在但左右极限不相等，则$x=x_0$为跳跃间断点

第二类

​ 第二类左右极限至少有一个不存在

​ 第二类间断点的极限不存在

• 无穷间断点

  左右极限至少有一个不存在且为无穷大,则$x=x_0$为无穷间断点

• 振荡间断点

  左右极限至少有一个不存在且振荡,则$x=x_0$为振荡间断点

四.习题总结

1.函数有界性

两个重要结论:

• 若$f(x)$在闭区间$[a,b]$上连续,则$f(x)$在闭区间$[a,b]$上有界

  ​ 闭区间连续函数必有界

• 若$f(x)$在开区间$(a,b)$内连续，且极限$\underset{x\to a^{+}}{\lim }f(x)$与$\underset{x\to b^{-}}{\lim }f(x)$存在,则函数$f(x)$在开区间$(a,b)$内有界

  ​ 左端点的右极限存在，右端点的左极限存在的开区间连续函数有界

2.其他解题经验

• 根据已有的条件去变形构造所需要的式子

比如这题：

在判断导数的时候,用了一个很常见一个等价变形做法就是的，除一个分母，再在分子上乘上

• 能和无穷乘起来得到常数的，极限一定是0

  ​ 例子看上面那题

• 分母极限为0，分式极限为常数，那么分子极限肯定也为0

  ​ 例子还是看上面那题

五.参考资料

部分图片来自《2022考研张宇考研数学基础30讲》、 《2022考研数学张宇数学题源探析经典1000题(数学一)》、《工科数学分析》(哈工大)