堆排序算法实现及其效率和稳定性分析（C语言）

Posted 2021-09-07 bfhonor

一、堆排序

（一）什么是“堆（Heap）”？

• 若n个关键字序列L[1…n] 满⾜下面某⼀条性质，则称为堆（Heap）：
  ① 若满足：L(i)≥L(2i)且L(i)≥L(2i+1) （1 ≤ i ≤n/2 ）—— 大根堆（大顶堆）
  ② 若满足：L(i)≤L(2i)且L(i)≤L(2i+1) （1 ≤ i ≤n/2 ）—— 小根堆（小顶堆）
  
  

（二）建立大根堆

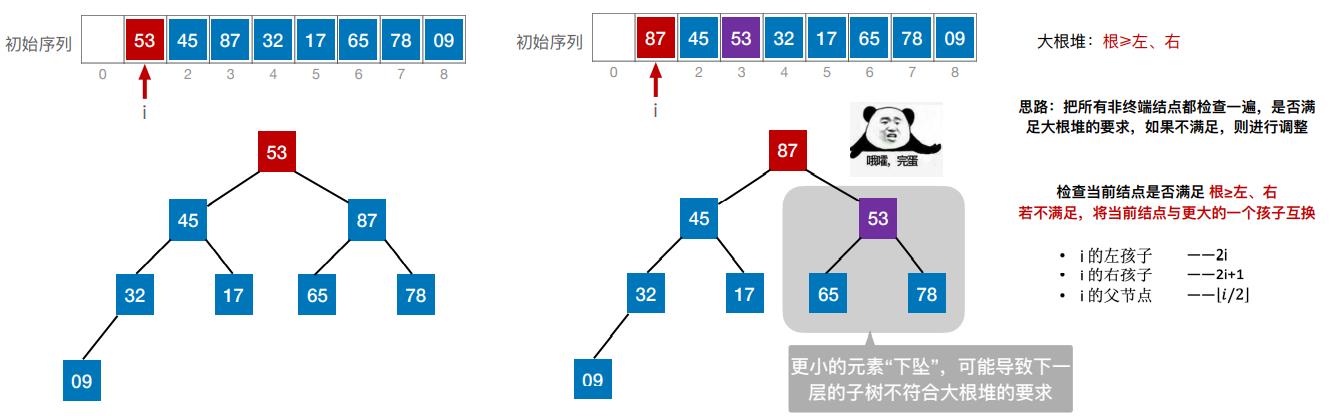
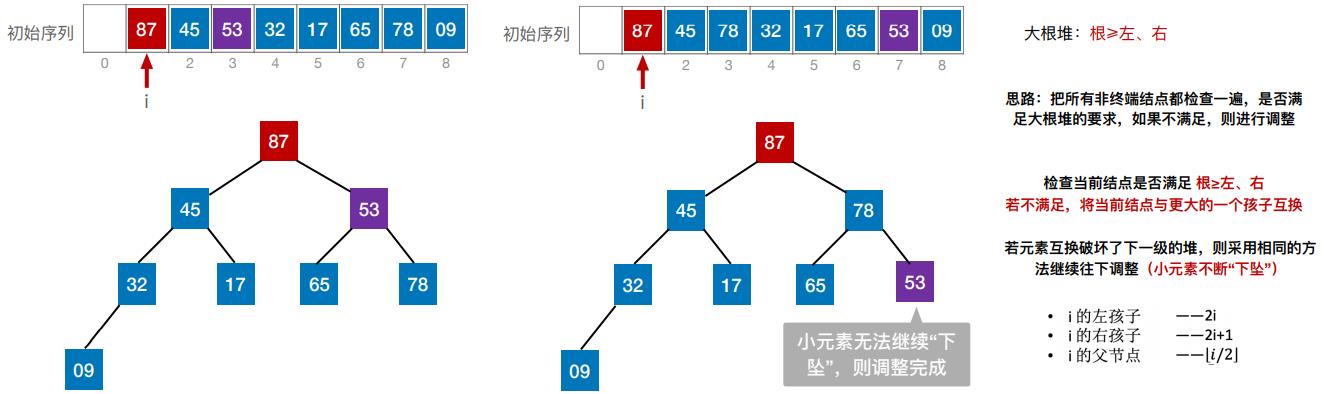
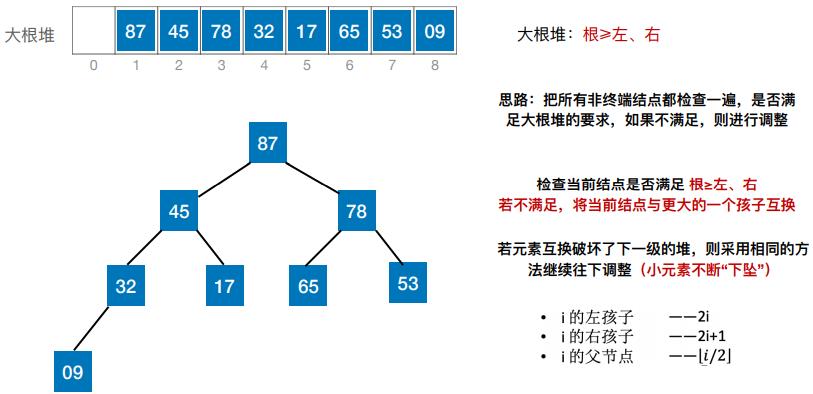
（二）建立大根堆（代码实现）

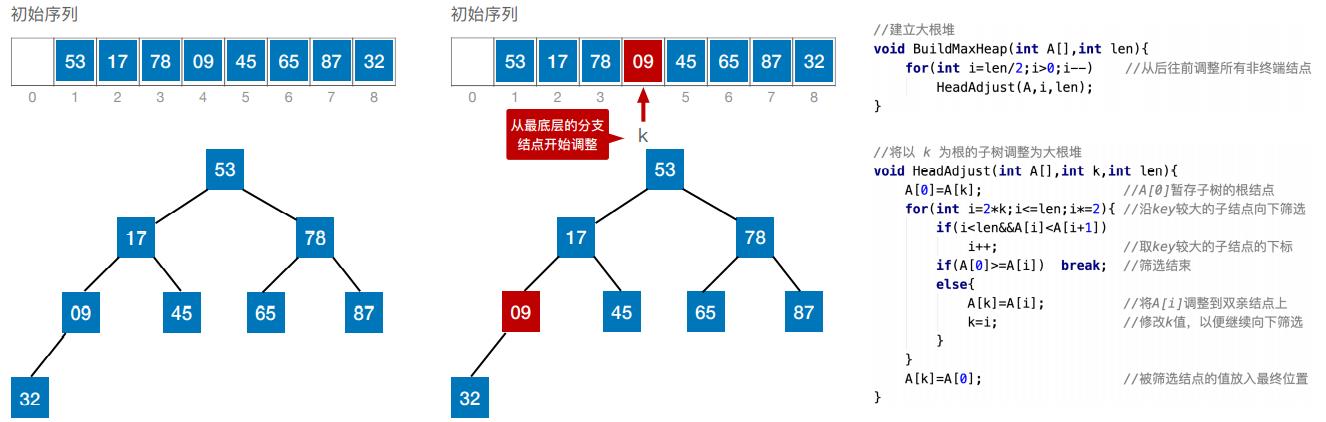
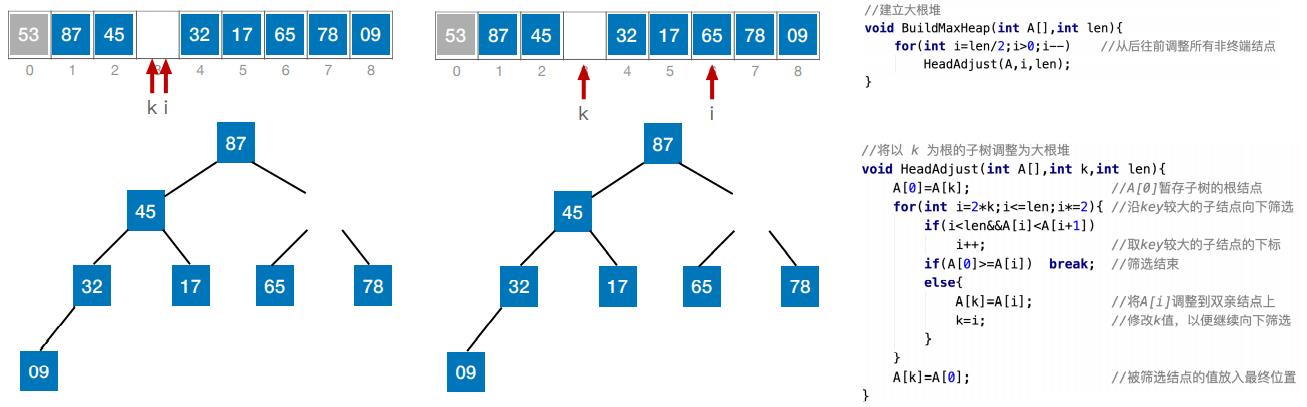
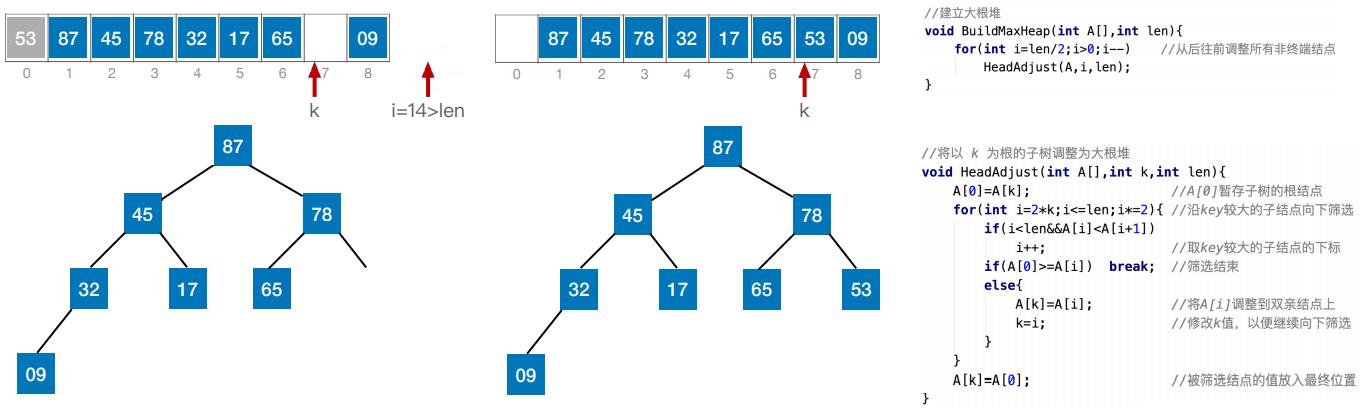
（四）基于大根堆进行排序

• 堆排序：每一趟将堆顶元素加入有序子序列（与待排序序列中的最后一个元素交换）
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  

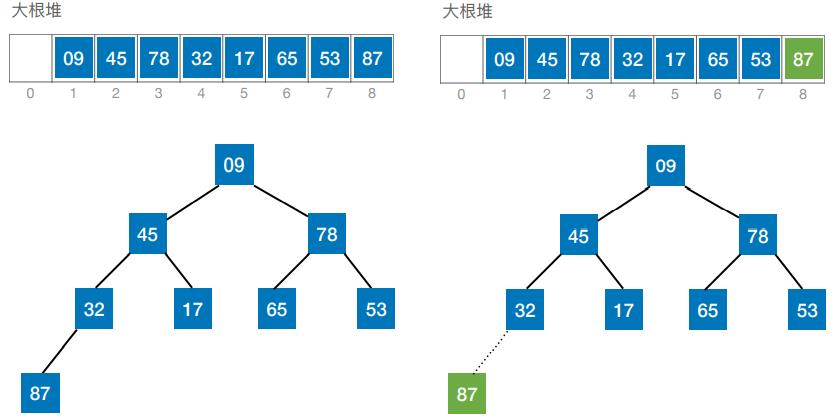
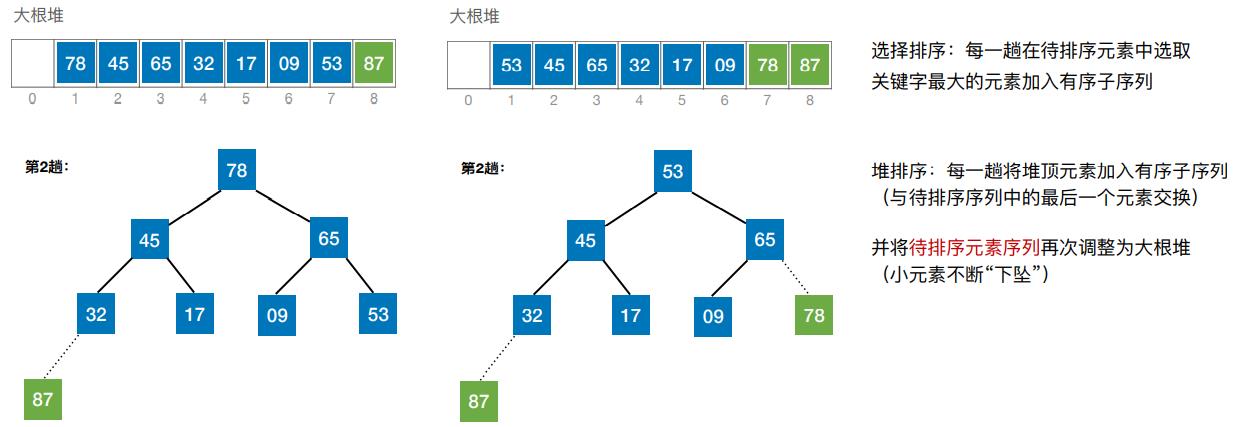
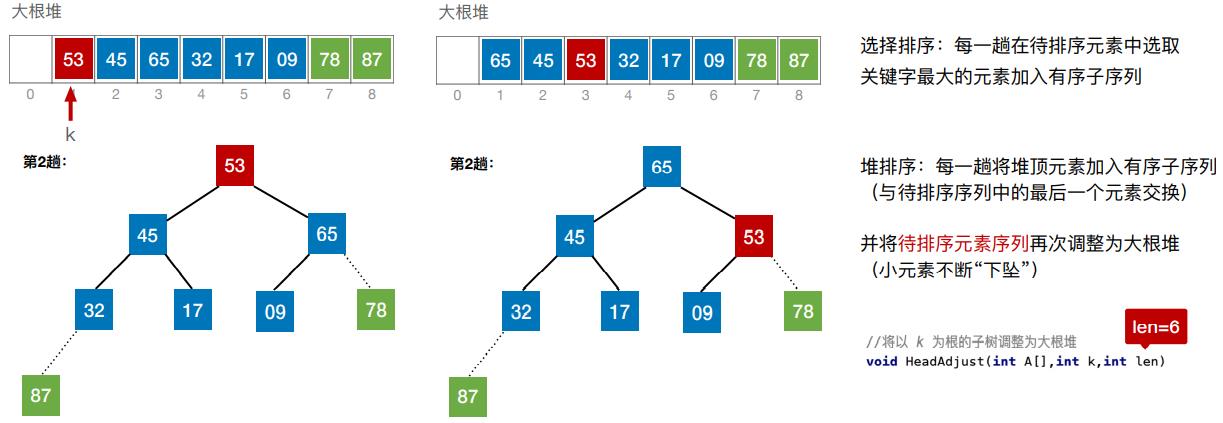
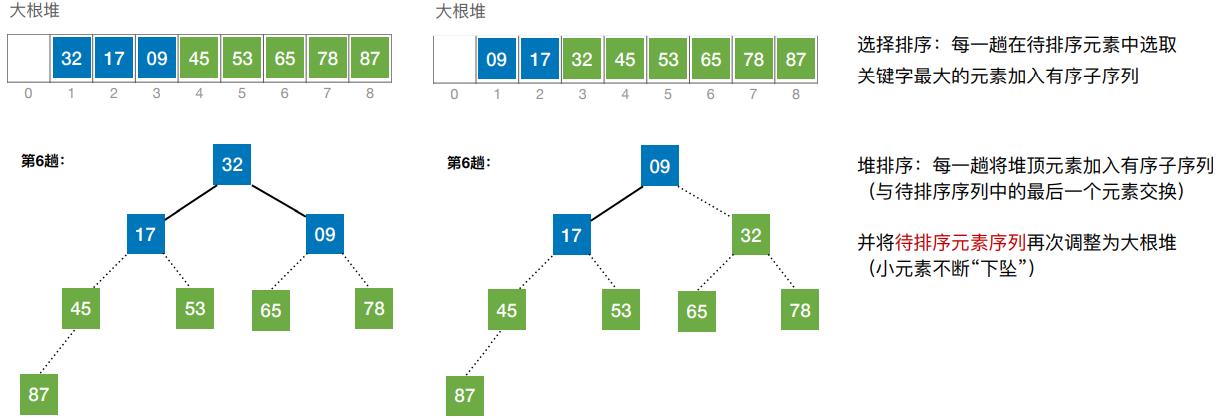
（五）算法效率分析

//建立大根堆
void BuildMaxHeap(int A[], int len){
	for(int i=len/2 ; i>0 ; i--)//从后往前调整所有非终端结点
		HeadAdjust(A,i,len);
}

//堆排序的完整逻辑
void HeapSort(int A[] , int len){
	BuildMaxHeap(A,len);	//初始建堆
	for(int i=len ; i>1 ; i--){//n-1趟的交换和建堆过程
		swap(A[i] , A[1]);	//堆顶元素和堆底元素交换
		HeadAdjust(A , 1 , i-1);//把剩余的待排序元素整理成堆
	}
}

//将以k为根的子树调整为大根堆
void HeapAdjust(int A[] , int k , int len){
	A[0]=A[k];	//A[0]暂存子树的根结点
	for(int i=2*k ; i<=len ; i*=2){//沿key较大的子结点向下筛选
		if(i<len && A[i]<A[i+1]){
			i++;	//取key较大的子结点的下标
		}
		if(A[0] >= A[i]){
			break;	//筛选结束
		}else{
			A[k]=A[i];//将A[i]调整到双亲结点上
			k=i;	//修改k值，以便继续向下筛选
		}
	}
	A[k]=A[0];		//被筛选结点的值放入最终位置
}

• 结论：一个结点，每“下坠”一层，最多只需对比关键字2次。
• 若树高为h，某结点在第 i 层，则将这个结点向下调整最多只需要“下坠” h-i 层，关键字对比次数不超过 2(h-i)
  
  
  

（六）稳定性

//堆排序的完整逻辑
void HeapSort(int A[] , int len){
	BuildMaxHeap(A,len);		//初始建堆
	for(int i=len ; i>1 ; i--){	//n-1趟的交换和建堆过程
		swap(A[i] , A[1]);		//堆顶元素和堆底元素交换
		HeadAdjust(A , 1 , i-1);//把剩余的待排序元素整理成堆
	}
}

• 结论：堆排序是不稳定的