前缀和 及 前缀和的变形

Posted 2021-09-07 晁棠

前缀和 及 前缀和的变形

---

前言

---

听完zngg的课后，我顿时醍醐灌顶，如同突破了瓶颈一般，感觉打开了一扇新世界的大门。现在稍微记录一下课堂笔记，届时便可反复复习。

前缀和

---

以往也是有了解过前缀和，但是也仅仅只是停留在表层，也就是最基本的题目，区间求和问题。
对于一段长度为n的数列a1,a2,…,an
定义前缀和为：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JhaYCiSn-1629269592509)(https://www.nowcoder.com/equation?tex=s_0%3D0%2Cs_i%3Ds_%7Bi-1%7D%2Ba_i%3D%5Csum_%7Bj%3D1%7D%5E%7Bi%7D%7Ba_i%7D “图片标题”)]
则当需要求区间[l,r]各个元素之和时，便需要计算
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GakTsFGq-1629269592511)(https://www.nowcoder.com/equation?tex=%5Csum_%7Bi%3Dl%7D%5E%7Br%7D%7Ba_i%7D%3Ds_r-s_%7Bl-1%7D “图片标题”)]
即可得出答案。

###前缀和的变形
其实这么几年来对于前缀和的了解我也仅仅只停留在上面的定义。在听了zngg的课之后，了解到了前缀和的变形之后，我发现其实是我的思想没有打开，就是没有理解到前缀和的思想。
对于上面最基本的前缀和的定义中，如果我们要求某个区间[l,r]的结果，我们先是算出[1,r]的结果，然后再抵消掉[1,l-1]所带来的影响，最后求出来的结果便是区间[l,r]的结果。
那什么时候能够将模型转化成前缀和的变形呢？当一个模型的某一刻的状态是从上一个状态所变化得来，且每一个状态可以通过某种变化使得这个状态带来的影响得以抵消，那么大部分就可以用转化成前缀和的变形了。

###例题

####智乃酱的区间乘积

这道题只是前缀和的一个小变形，前缀积。求一个区间[l,r]的乘积，那么只要先预处理出[1,r]的乘积，再除以[1,l-1]的乘积，那么便能够得到[l,r]之间的乘积了。
注意，这道题在取模的条件下不能够直接除噢，除以[1,l-1]的乘积要变为乘以[1,l-1]的乘积的逆元。
代码：

#include <iostream>
#include <stdio.h>
#include <cstdio>
#include <stdlib.h>
#include <string>
#include <string.h>
#include <cstring>
#include <math.h>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <map>
#include <algorithm>
#define _for(i,a,b) for(int i=(a) ;i<=(b) ;i++)
#define _rep(i,a,b) for(int i=(a) ;i>=(b) ;i--)
#define mst(v,s) memset(v,s,sizeof(v))
#define IOS ios::sync_with_stdio(false)
#define ll long long
#define INF 0x7f7f7f7f7f7f7f7f
#define inf 0x7f7f7f7f
using namespace std;
const ll mod=1e9+7;
const int N=1e5+5;
int n,t;
ll a[N];
ll qmi(ll a,ll k,ll p)
{
    ll res=1;
    while(k)
    {
        if(k&1) res=res*a%p;
        k>>=1;
        a=a*a%p;
    }
    return res;
}
void ready()
{
    IOS;
    cin>>n>>t;
    a[0]=1;
    for(int i=1;i<=n;i++)
    {
    	cin>>a[i];
    	a[i]=(a[i-1]%mod)*(a[i]%mod)%mod;
        a[i]=a[i]%mod;
	} 
}
void work()
{
	int l,r;
	cin>>l>>r;
	cout<<(a[r]%mod)*qmi(a[l-1],mod-2,mod)%mod<<'\\n';
}
int main()
{
    ready();
    while(t--)
    work();
    return 0;
}

####牛牛的猜球游戏

思路：题目要求从第l个操作开始做，然后一直做到第r个操作结束后的状态。这里每一个操作的相对独立，我们就思考，我们能不能用从第1个操作做到第r个操作得到的状态，然后再抵消掉第1个操作做到第l-1个操作得到的状态所带来的影响，以此变成前缀和的变形。
答案是可以的。
如果说要求[l,r]的操作，那么也就是当开始做第l个操作时，我们的球必须是0,1,…,9这个序号排序的。那我们就思考，如果已知从序号排列为0,1,…,9做到第l-1状态后的结果，如何构造一个序号的顺序，使得当我从第1个操作做到第l-1个操作之后，球的序号排序为：0,1,…,9。
假设1,2,3通过变化后的结果为2,3,1。我们得知变化后的2在第一位，变化后的3在第二位，变化后的1在第3位，那么我们可以推出，当3,1,2通过相同的变化之后，得到的结果便为1,2,3
通过这样子就能够抵消掉[1,l-1]的操作下带来的影响啦。
代码：

#include <iostream>
#include <stdio.h>
#include <cstdio>
#include <stdlib.h>
#include <string>
#include <string.h>
#include <cstring>
#include <math.h>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <map>
#include <algorithm>
#define _for(i,a,b) for(int i=(a) ;i<=(b) ;i++)
#define _rep(i,a,b) for(int i=(a) ;i>=(b) ;i--)
#define mst(v,s) memset(v,s,sizeof(v))
#define IOS ios::sync_with_stdio(false)
#define ll long long
#define INF 0x7f7f7f7f7f7f7f7f
#define inf 0x7f7f7f7f
using namespace std;
int n,T;
int a[100005][10];
void ready()
{
    IOS;
    cin>>n>>T;
    for(int i=0;i<10;i++) a[0][i]=i;
    for(int i=1;i<=n;i++)
    {
    	for(int j=0;j<10;j++) a[i][j]=a[i-1][j];
    	int l,r;
    	cin>>l>>r;
    	swap(a[i][l],a[i][r]);
	}
}
void work()
{
	int l,r;
	cin>>l>>r;
	int t[10];
	for(int i=0;i<10;i++)
	  t[a[l-1][i]]=i;
	for(int i=0;i<10;i++)
	  cout<<t[a[r][i]]<<' ';
	cout<<'\\n';
	return ;
}
int main()
{
    ready();
    while(T--)
      work();
    return 0;
}

####智乃酱的双塔问题

思路：
这道题我们可以想到用dp去做，dp[i][0]表示从第1层走到第i层左塔的方案数，dp[i][1]表示从第1层走到第i层右塔的方案数。
dp式子如下:
dp[i][0]=dp[i-1][0] + “i-1层右塔有梯子到第i层左塔”?dp[i-1][1]:0 ;
dp[i][1]=“i-1层左塔有梯子到第i层右塔”?dp[i-1][0]:0 + dp[i-1][1] ;

其实可以发现，这个就是一个矩阵，如果写成矩阵形式如下：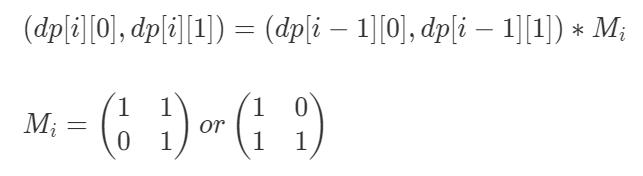

又dp[1][0]=1,dp[1][1]=1，所以我们可以得到：

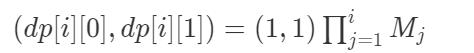
根据这个式子，就可以的得到第1层每一层的方案数了。
对于l到r层的方案数，那如何抵消掉第1层到第l-1层的方案呢？
那就求出第l-1层的逆矩阵即可。那么如何求逆矩阵？
对于一个2*2的矩阵$A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$,其伴随矩阵$A^T=\left(\begin{array}{cc}d& -b\\ -c& a\end{array}\right)$,逆矩阵为$\frac{A^T}{|A|}$,而在本题，$\left|A\right|$恒等于1，则M任意一个矩阵$M_i=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$的逆矩阵为$M_i^{-1}=\left(\begin{array}{cc}d& -b\\ -c& a\end{array}\right)$。

随后就可以解题啦！
（我还没有调好我的代码，先不贴出来了555）