[数值计算-3]:误差的种类误差传播误差分析
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[数值计算-3]:误差的种类误差传播误差分析相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119790035
目录
第1章 误差与有效数值(误差度量的数学模型)
1.1 什么是误差(绝对误差)
实际值与理论值的差,称为误差。


1.2 什么是相对误差


1.3 绝对误差与相对误差的比较
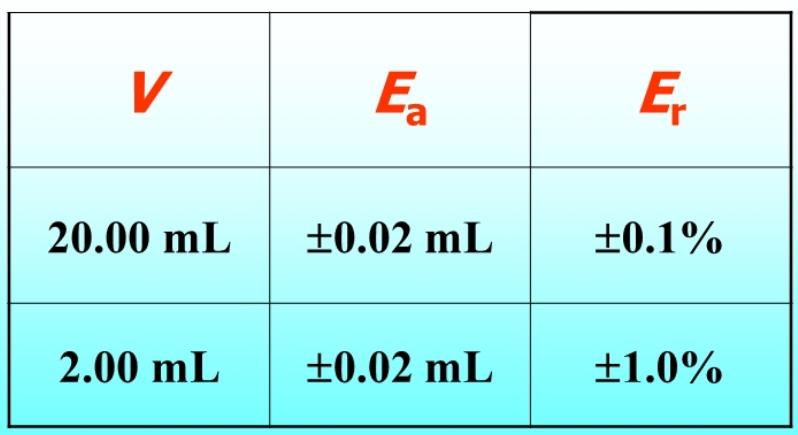

1.4 什么是有效数值
有效数字是指在分析工作中实际能够测量到的数字。能够测量到的是包括最后一位估计的,不确定的数字。
我们把通过直读获得的准确数字叫做可靠数字;
把通过估读得到的那部分数字叫做存疑数字。
把测量结果中能够反映被测量大小的带有一位存疑数字的全部数字叫有效数字。
测得物体的长度5.15cm。数据记录时,我们记录的数据和实验结果真值一致的数据位便是有效数字。
另外在数学中,有效数字是指在一个数中,从该数的第一个非零数字起,直到末尾数字止的数字称为有效数字,如0.618的有效数字有三个,分别是6,1,8。
第2章 误差的分类与来源
2.1 人为过失误差
是计算过程中,人为错误造成的误差,这种误差是可以避免的,也必须避免。

数值计算探讨的误差是非过失误差!!!
2.2 模型误差(建模误差)

2.3 测量误差

备注:几乎所有的测量数据都是不准确的,与真值之间都有存在偏差。
提升测量工具和测量方法。
2.4 截断误差 (方法误差)

截断误差来自于在计算机实现中,用有限序列替代无线序列,
截断误差来自于把复杂问题简单化造成的误差。
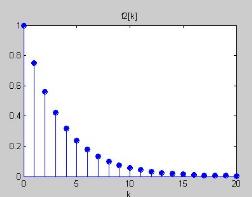
2.5 四舍五入误差

2.6 计算机浮点数长度限制引入的误差
这种误差,本质上也是一种四舍五入误差。
第3章 误差的传播
3.1 什么是误差的传播

误差的传播是指在数学运算过程中,需要经过一次次的数学函数变换,由于参与计算的源数据本身有误差,导致变换后的结果数据也产生误差,这种误差有可能由于运算本身会放大,或因为多个参与运算的源数据的误差的叠加,导致更大的误差。

这就是误差的传播,运算次数越多,误差被传播得越远,误差被放大的可能性就越大。因此,要尽量降低运算的次数。这种由于多次函数变换导致误差的传导,称为误差的传播。
3.2 加法和减法运算的绝对误差

备注:加法运算结果的绝对误差是所有初始输入误差的累计和(叠加)
如下图展示:
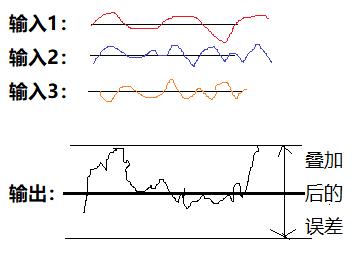
也就是说,参与运算的输入元素的个数越多,结果的误差越大。
3.3 加法运算的相对误差
相对误差 = 绝对值/精确值

加法的相对误差限,是任意一个输入元素相对误差的最大值!!!
加法运算的相对误差是稳定的、受控的!!!
3.4 减法运算的相对误差

3.5 乘法运算的误差

(1)绝对误差:其传播系数是输入参数的数值的绝对值,因此乘法运算,要避免使用非常大的数值,否则会导致结果的绝对误差被无限放大。或者所要避免用一个大数 * 小数 =》中等的数据,虽然输出结果是中数,但绝对误差与大数相乘,导致绝对误差很大。
(2)相对误差:是两个输入参数相对误差的代数和。乘法的相对误差是稳定的。
3.6 除法运算的误差

由于误差会传播,因此好的算法要尽可能降低运算的次数,防止误差无限制的放大。
当然,运算次数少,还可以降低算法的执行时间。
3.7 四则运算的传播误差的简化估算

3.8 函数运算的传播误差的简化估算

第4章 算法误差的特性
4.1 稳定性

稳定性描述的是输出误差与输入关系的一种工具。
如果输出误差与输入误差有确切的关系,说明说算法的误差是稳定的。
4.2 收敛性
这是分析输出误差与输入误差关系的另一种工具。
它反映了输出是不是被限制在某个门限内,而不会无限制的放大。这就是误差的收敛性。
第5章 误差的改善
除了人为错误造成的误差,误差是无法避免的,只能改善,通过改善,降低误差的数值。
另外,每个工程问题,都有大量的不同的算法,不同的算法的误差也是不相同的,通过改善,降低误差的数值。
误差传输的改善主要针对误差来源进行性,大部分误差的来源,本质的原因是计算机对数据的表达是近似值。
5.1 改善测量精度
提高原始测量数据的精度和有效数字。
5.2 改善存储精度
改善计算机存储数据的精度,从32bit提升到64bit。
5.3 改善运算模型
(1)案例1:

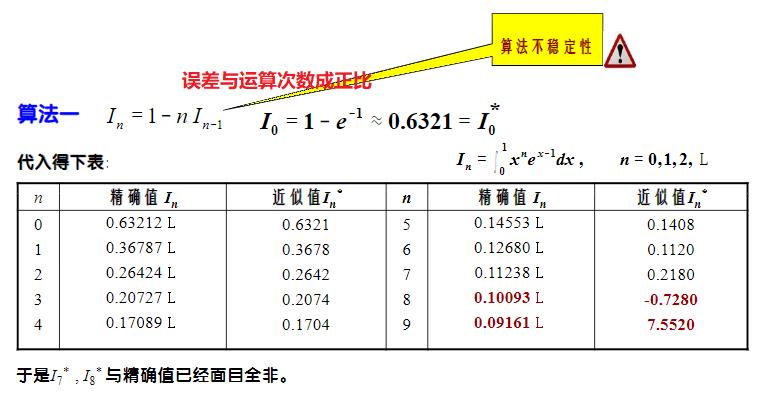
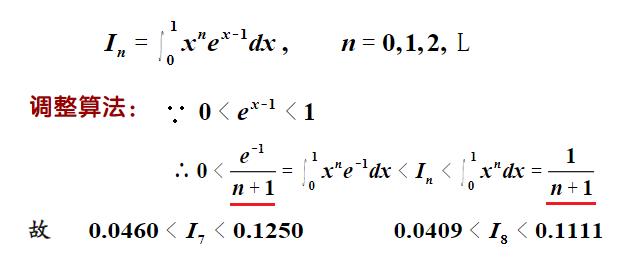
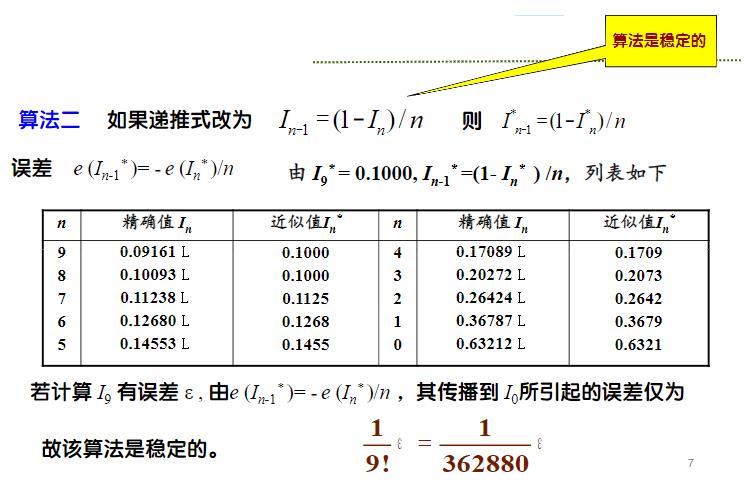
(2)案例2:

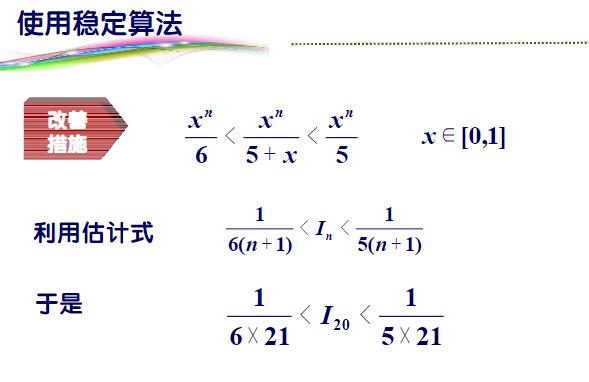
(3)案例3:


(4)案例4

5.4 概述运算过程


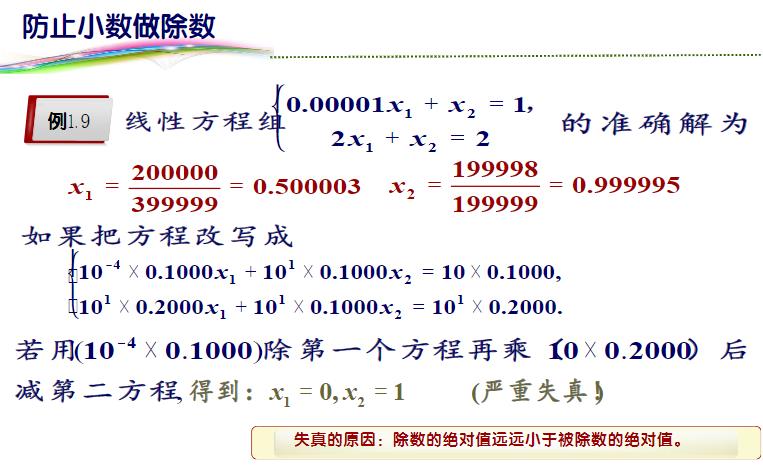

作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119790035

以上是关于[数值计算-3]:误差的种类误差传播误差分析的主要内容,如果未能解决你的问题,请参考以下文章