[数值计算-5]：一元二次非线性方程求解 - 解析法直接求解

Posted 2021-09-07 文火冰糖的硅基工坊

 作者主页(文火冰糖的硅基工坊)：https://blog.csdn.net/HiWangWenBing

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/119806022

---

目录

1.  一元二次非线性方程(直线方程）

1.1 什么是一元二次非线性方程(抛物线方程）

1.2 非线性函数

1.3 一元二次非线性方程（抛物线方程）的几何函数

1.4 一元一次线性函数的特点

1.5 一元二次非线性函数的重要意义

1.6  一元二次线性函数的数值表达（excel）

2.  一元二次线性函数求解

2.1 求一元二次线性方程根

2.3 高次非线性方程求解问题

---

---

1.  一元二次非线性方程(直线方程）

1.1 什么是一元二次非线性方程(抛物线方程）

只含有一个未知数（一元），并且未知数项的最高次数是2（二次）的整式方程叫做一元二次方程。

一元二次方程经过整理都可化成一般形式ax²+bx+c=0（a≠0）。其中ax²叫作二次项，a是二次项系数；bx叫作一次项，b是一次项系数；c叫作常数项。

1.2 非线性函数

线性函数是一次函数的别称，则非线性函数即函数图像不是一条直线的函数。非线性函数包括指数函数、幂函数、对数函数、多项式函数等等基本初等函数以及他们组成的复合函数

1.3 一元二次非线性方程（抛物线方程）的几何函数

y = f(x) = ax²+bx+c

因此，一元二次方程的方程求解，实际上是一元二次函数（抛物线）与x轴的交点。

1.4 一元一次线性函数的特点

（1）有可能有无方程解、或一个方程解或两个方程解（最多）

（2）当a>0, 有最小值

（3）当a<0, 有最大值

（4）当a = 0， 无极值

1.5 一元二次非线性函数的重要意义

一元二次非线性函数被广泛应用于最小二乘法求误差的最小值，或者说一元二次非线性函数是最小二次函数的最基本的组成单元。

深度学习的Loss损失函数的基本组成单元也是一元二次函数。

1.6  一元二次线性函数的数值表达（excel）

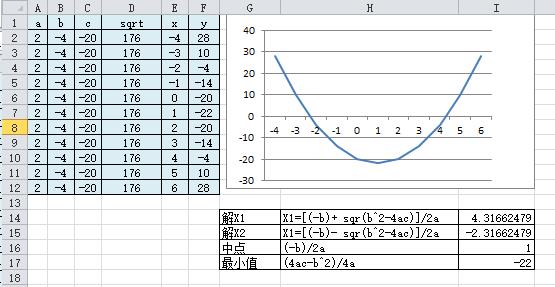
2.  一元二次线性函数求解

2.1 求一元二次线性方程根

一元一次方程求解非常简单，可以直接通过“解析法”获取方程的根，不需要进行反复迭代。

一元一次方程只有一个根: 

2.2 一元二次线性函数的极值

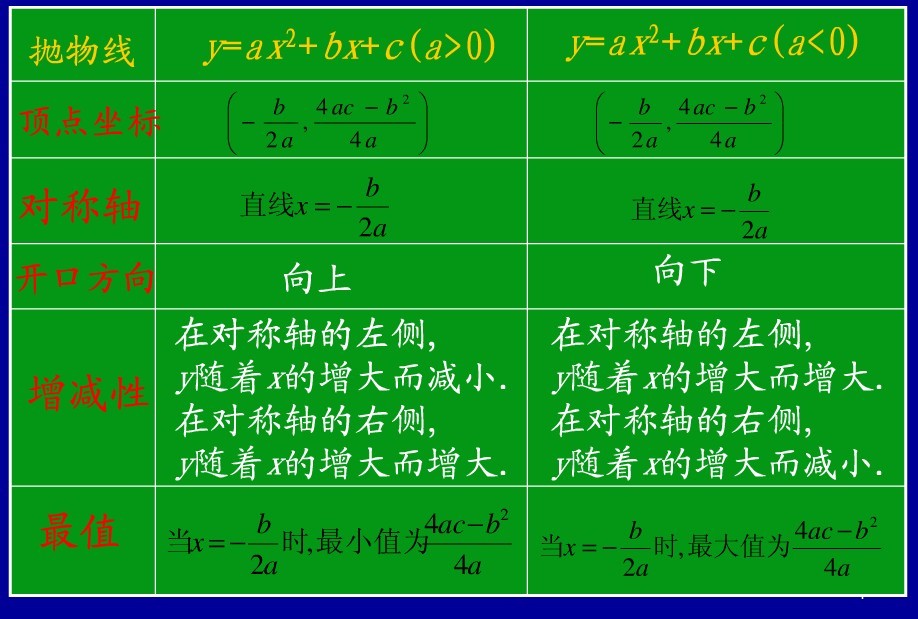
2.3 高次非线性方程求解问题

早在16世纪就找到了三次、四次方程的求根公式。

但直到19世纪才证明了n>=5次的一般代数方程式是不能用代数公式求解的。

因此需要研究用数值方法求得满足一定精度的高次非线性方程程式的近似解。

---

作者主页(文火冰糖的硅基工坊)：https://blog.csdn.net/HiWangWenBing

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/119806022