数据结构与算法之深入解析如何确定单链表有环并求环的入口和长度

Posted 2021-09-07 Forever_wj

一、检测单链表中存在环

① 环的定义

• 单链表中结点都是一个结点指向下一个结点这样一个一个链接起来的，直到尾结点的指针域没有指向，单链表就到此结束。
• 链表有环的定义是，链表的尾结点的指针域并为空，指向了链接中间的某个结点，这样就形成环，遍历单链表就会死循环，这是因为破坏了结束条件。
• 如下所示：如果单链表有环，则在遍历时，在通过结点 J 之后，会重新回到结点 D：

② 快慢指针检测

• 设两个工作指针，一个快一个慢，如果有环的话，它们会必然在某点相遇。
• 算法的思想是：设定使用两个指针，fast 与 slow，它们起始都位于链表的头部。随后，slow 指针每次向后移动一个位置，而 fast 指针向后移动两个位置。如果链表中存在环，则 fast 指针最终将再次与 slow 指针在环中相遇。
• 如下图所示，设链表中环外部分的长度为 a。slow 指针进入环后，又走了 b 的距离与 fast 相遇。此时，fast 指针已经走完了环的 n 圈，因此它走过的总距离为 a+n(b+c)+b=a+(n+1)b+nc：

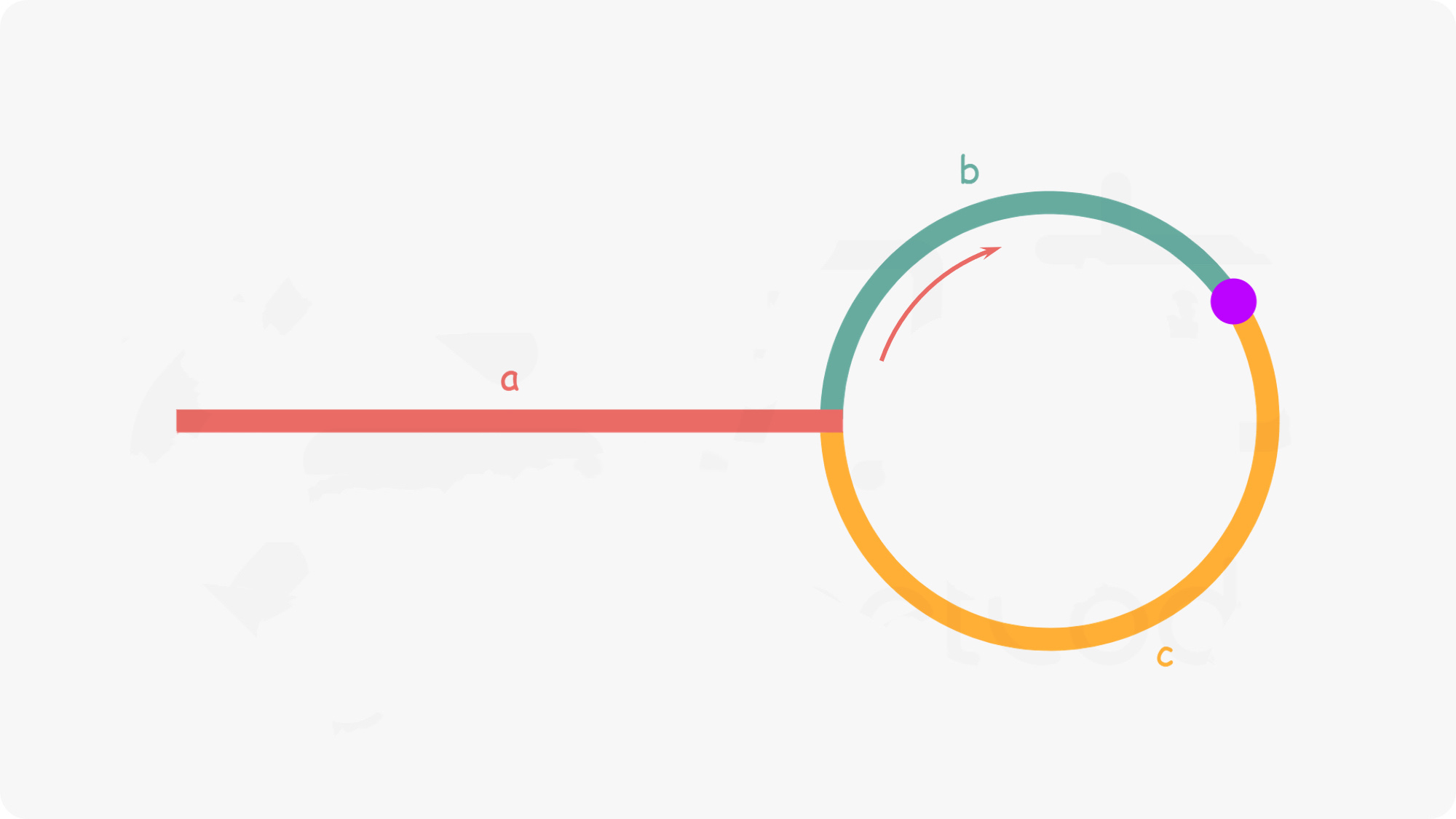
• 任意时刻，fast 指针走过的距离都为 slow 指针的 2 倍。因此，有 a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c)，有了 a=c+(n−1)(b+c) 的等量关系，会发现：从相遇点到入环点的距离加上 n−1 圈的环长，恰好等于从链表头部到入环点的距离。
• 因此，当发现 slow 与 fast 相遇时，再额外使用一个指针 ptr。起始，它指向链表头部；随后，它和 slow 每次向后移动一个位置。最终，它们会在入环点相遇。

	/*
	使用快慢指针判断单链表是否存在环
	使用slow、fast 2个指针，slow慢指针每次向前走1步，fast快指针每次向前走2步，
	若存在环的话，必定存在某个时候 slow = fast 快慢指针相遇。
	list 带头结点的单链表
	返回值 > 0:存在环返回环的位置	0:不存在环
	*/
	int IsLoopLinkList(LinkList list) {
		// 空指针
		if (list == NULL) {
			return 0;
		}
		// 只有头结点,没有元素
		if (list->next == NULL) {
			return 0;
		}
		Node* slow = list;
		Node* fast = list;
		int loc = 0;
		while (1) {
			if (fast->next == NULL) {
				//快指针 到底链表尾结点说明 没有环，此时slow 指向中间结点
				return 0;
			} else {
				if (fast->next != NULL && fast->next->next != NULL) {
					fast = fast->next->next;
					slow = slow->next;
				} else {
					fast = fast->next;
				}
			}
			// 某个时刻快慢指针相遇，说明此处存在环
			if (slow == fast) {
				return (slow - list) / sizeof(Node);
			}
	
		}
		return 0;
	}

③ 结点路径计算

• 设两个工作指针 p 和 q，p 总是向前走，但 q 每次都从头开始走，对于每个结点，看 p 走的步数是否和 q 一样。
• 比如：p 从 A 走到 D，用了 4 步，而 q 则用了 14 步，因而步数不等，出现矛盾，存在环。
• 以上面图片的环来说，p 总是向前走，而 q 每次都从头开始走，它们都从结点 A 出发：
• • 第 1 次，p 走到 B 点，这时 p 走了 1 步，此时 q 从头开始走，走到 B 点也用了 1 步；
• • 第 2 次，p 走到 C 点，这时 p 走了 2 步，此时 q 从头开始走，走到 C 点也用了 1 步；
• • ……
• • 第 12 次，p 走到 J 点，这时 p 走了 12 步，此时 q 从头开始走，走到 J 点也用了 12 步；
• • 第 13 次，p 走到 D 点， 这时 p 走了 14 步，此时 q 从头开始走，走到 D 点只用了 3 步；p 和 q 走到相同个位置上的步数不相等，说明链表存在环。
• • 如果一直到 p == null 的时候还未出现步数不相等的情况，那么就说明不存在链表环。

④ 标记法

• 可以遍历这个链表，遍历过的结点标记为 Done，如果当目前准备遍历的结点为 Done 的时候，那么存在环，否则准备检测的结点为 Null 时，遍历完成，不存在环。

⑤ 哈希表法

• 每个结点是只读的，不可以做标记呢？那可以另外开辟一个哈希表，每次遍历完一个结点后，判断这个结点在哈希表中是否存在，如果不存在则保存进去，如果存在，那么就说明存在环。
• 要是取到 Null 还没有重复，那么就是不存在了，这个哈希表可以在 Java 语言中可以用 HashMap 实现。

	public class Solution {
	    public ListNode detectCycle(ListNode head) {
	        ListNode pos = head;
	        Set<ListNode> visited = new HashSet<ListNode>();
	        while (pos != null) {
	            if (visited.contains(pos)) {
	                return pos;
	            } else {
	                visited.add(pos);
	            }
	            pos = pos.next;
	        }
	        return null;
	    }
	}

二、检测单链表环的入口

• 对单链表是否存在环进行检测，那么：
• • 一个单链表，如果有环，如何求环的入口？
• • 一个单链表，如果有环，如何求环的长度？
• 链表这种结构，可以通过“指针”将一组零散的内存块串联起来。那么单链表，如果有环是一个什么情况呢？
• 单链表中如果存在环，一定有且只有一个入口点，进去了就别想出来，接下来看看如何找到这个环的入口。

① 哈希法

• 哈希法的思路很简单，如果单链表上有环，那必然有一个链表上靠后的结点的 next 指针，指向了一个靠前的结点。
• 那么就可以通过一次循环加一个 Set 的辅助集合，来在每次循环的时候，判断结点是否在 Set 中，如果没有则将结点存入 Set 并继续循环，有则找到了链表的入口。

	ListNode detectCycle(ListNode head) {
	  Set<ListNode> visited = new HashSet<>();
	  ListNode node = head;
	  while(node != null) {
	    if (visited.contains(node))
	      return node;
	    visited.add(node);
	    node = node.next;
	  }
	}

• 哈希法的方式相对暴力，但是很好理解，只是需要额外消耗一个 Set 结构的空间，所以空间复杂度是 O(n)，同时它也是一种检测单链表是否有环的解法。

② 双指针法（Floyd 算法）

• 在上文中，在检测单向链表是否有环的解法中，有一个比较经典的双指针来辅助计算，就是快慢指针。解题思路就是使用 2 个指针，快指针每次走 2 步，慢指针每次走 1 步，如果链表有环，那么它们肯定可以在环中相遇。就像两个人在圆形的赛道上赛跑，一个跑的快另一个跑的慢，最终肯定是跑的快的人，追上了跑的慢的。不过想用双指针来确定单链表环的入口，思路上还有一些绕。
• 简单来说，当快、慢两个指针首次相遇后，再用两个指针，指针 A 指向首次相遇的结点，指针 B 移动到单链表的头结点，然后两个指针分别每次向前移动 1 步，最终相遇的地方，就是单链表成环的入口。
• 先来说说思路，首先假设环足够大，存在 3 个关键结点：链表头结点、环入口结点、快慢指针首次相遇结点，通过这三个点可以将指针移动的路径，分为 3 个区域。

• 当找到首次相遇点后，使用两个指针，指针 A 指向首次相遇的点，指针 B 指向链表头，两个指针继续同时向前走，每次走 1 步，最终会在链表环的入口处相遇。

• 既然 A、B 两个指针，每次走 1 步，最终相遇的点，就是环的入口，那么从步长来说 F = b，但是为什么它们是相等的呢？Leetcode 給出一个 F = b 的指导公式，很清晰，可以参考一下：

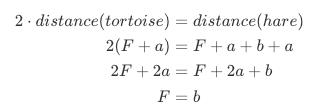
• 为了简化问题，只考虑环很大的情况，最少是 2 倍于表头结点到环入口结点的距离：
• • 首先，每次快指针走 2 步，慢指针走 1 步，假设慢指针走了 F 步走到了环的入口处，此时快指针走了 2F 步；
• • 其次，当慢指针在环的入口点时，此时快指针距离入口点，已经走了 F 步了，多说一句 F 就是链表头到环入口结点的距离。此时慢指针（slow） 和快指针（fast）都在环上，可将环分为 n（红色）和 b（蓝色） 两个区域，此时 b == F；

• • 再次，快、慢指针继续向前走，快指针想要追上慢指针，只有一种情况，就是慢指针走了 b 步，而快指针走了 2b 步，跨越了环入口结点。可以简单理解这个圆环，以环入口点到圆心为轴，翻转了一次。

• • 最后，到这里应该就清晰了，剩余的 b 区域，其实就等于 F 区域，所以再用两个指针，分别在相遇结点和头结点继续向前走，每次走 1 步，最终两个指针会在入环点相遇。

	public ListNode detectCycle(ListNode head) {
	  ListNode slow = head, fast = head;
	  
	  while (true) {
	    if (fast == null || fast.next == null)
	      return null;
	    
	    slow = slow.next;
	    fast = fast.next.next;
	    
	    if (fast == slow)
	      break;
	  }
	  
	  fast = head;
	  while (slow != fast) {
	    slow = slow.next;
	    fast = fast.next;
	  }
	  return fast;
	}

• 上文说到，为了简化问题，前提条件是环很大，那么在环很小的时候呢？大与小本身就是一个相对的概念，在链表成环的场景下，说环很大的意思是在慢指针走到入环结点时，快指针还没有走完一圈。也就是说，要满足这个条件 2F < C，F 为链表头结点到入环结点的长度，C 为环长度，这里面有两个变量。要么真的是个很大的环，要么 F 的长度很短，都可以说是“小环”，此时慢指针走到入环结点时，快指针已经在环内空转了 n 圈了。
• 环小的情况，其实和环大的情况是一样的，只是人为的觉得快指针多跑了很多圈，好像更复杂一些，举两个思考模型来帮助思考：
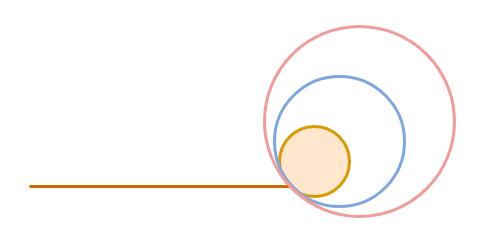
• • 小环展开成大环：可以将小环循环铺开，虚拟展开成一个大环去理解；

• • 从单链表上，去掉环内空转的长度，其实不关心链表表头到入环结点的实际距离，只是为了求入环点，所以可以直接将快指针在环内空转的距离，从单链表上去掉。

• 这两个思考模型，都是为了帮助我们更好的理解和抽象问题，其实在“小环”的场景下，慢指针走到入环结点时，快指针已经在环内空转了很多圈，所以其实这并不影响计算的结果。找到入环结点，那么环的长度的算法，就是单链表求长度的算法。