剑指 Offer 49. 丑数

Posted 2021-09-07 aaaaaaaWoLan

剑指 Offer 49. 丑数

我们把只包含质因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。

示例:

输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。

说明:

1. 1 是丑数。
2. n 不超过1690。

**思路：**因为丑数的质因子只有2、3、5，所以大一点的丑数一定可以由2或3或5相乘得到

使用三指针p2、p3、p5，创建丑数数组从小到大存放丑数，p2、p3、p5则按从小到大的顺序遍历数组一开始p2、p3、p5都指向第一个丑数1，后来比较2 *p2、3 *p3、5 *p5的大小，取最小的那个作为下一个丑数，并判断新的丑数是否与2 *p2、3 *p3、5 *p5相等，如果相等，则对应的指针向后走，这么做是为了让p2、p3、p5依次从小到大遍历丑数，然后按照从小到大的顺序找出丑数

以n=10为例：

一开始，p2、p3、p5都指向1，随后寻找第二个丑数

第二步判：断2 *ugly[p2]、3 *ugly[p3]、5 *ugly[p5]中的最小值，易知2最小，所以第二个丑数就为2，之后判断2 *ugly[p2]、3 *ugly[p3]、5 *ugly[p5]中谁等于新的丑数，2 *ugly[p2]与其相等，所以p2++，p3、p5不动

第三步：判断2 *ugly[p2]、3 *ugly[p3]、5 *ugly[p5]中的最小值，此时ugly[p2] = 2，uglyp3]和ugly[p5]都等于1，所以很明显3 *ugly[p3]最小，下一个丑数即为3，且p3++，p5不动(注意p2、p3、p5不一定要各自对应2、3、5的倍数的丑数)

第四步：判断2 *ugly[p2]、3 *ugly[p3]、5 *ugly[p5]中的最小值：4<5<6，所以2 *ugly[p2]最小，下一个丑数即为4，并且p2++

第五步：判断2 *ugly[p2]、3 *ugly[p3]、5 *ugly[p5]中的最小值：5<6=6，所以5 *ugly[p5]最小，下一个丑数即为5，并且p5++

第六步：判断2 *ugly[p2]、3 *ugly[p3]、5 *ugly[p5]中的最小值：6=6<10，所以此时2 *ugly[p2]和3 *ugly[p3]同为最小值，下一个丑数即为6，此时2 *ugly[p2]、3 *ugly[p3]均等于新的丑数6，所以p2、p3均++

第七步：判断2 *ugly[p2]、3 *ugly[p3]、5 *ugly[p5]中的最小值：8<9<10，所以此时2 *ugly[p2] = 8为最小值，下一个丑数即为8，p2++

第八步：判断2 *ugly[p2]、3 *ugly[p3]、5 *ugly[p5]中的最小值：9<10=10，所以此时3 *ugly[p3]为最小值，下一个丑数即为9，p3++

第九步：判断2 *ugly[p2]、3 *ugly[p3]、5 *ugly[p5]中的最小值：10=10<12，所以此时5 *ugly[p5]于2 *ugly[p2]同为最小值，下一个丑数即为10，p2、p5均++

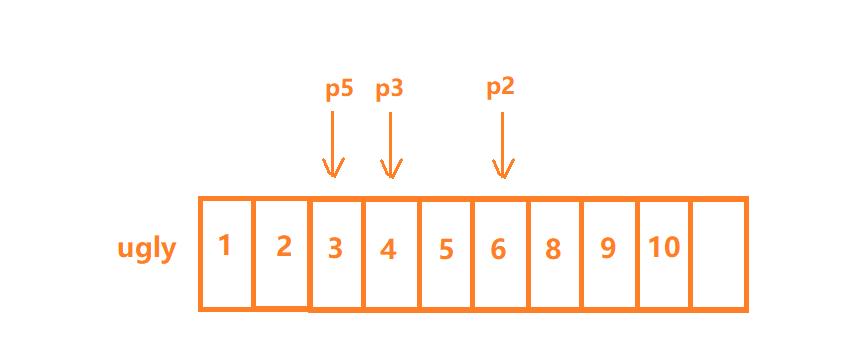
第十步：判断2 *ugly[p2]、3 *ugly[p3]、5 *ugly[p5]中的最小值：12 = 12 < 15，所以此时3 *ugly[p3]于2 *ugly[p2]同为最小值，下一个丑数即为12，p2、p3均++

到这里就已经找到第10个丑数了，也就是12

代码：

int min(int x, int y)
{
    if (x > y)
    return y;
    else
    return x;
}

int nthUglyNumber(int n){
    int p2,p3,p5,count;
    p2 = p3 = p5 = count = 0;
    int*ugly = (int*)malloc(sizeof(int) * n);
    ugly[count++] = 1;
    while (--n)
    {   
        ugly[count++] = min(ugly[p5]*5, min(ugly[p3]*3, ugly[p2]*2));


        //不能用else if，不然会有丑数重复
        if (ugly[p2] * 2 == ugly[count - 1])
        {
            p2++;
        }
        if (ugly[p3] * 3 == ugly[count - 1])
        {
            p3++;
        }
        if (ugly[p5] * 5 == ugly[count - 1])
        {
            p5++;
        }
    }

    return ugly[count - 1];
}