机器学习笔记——Regression 1
Posted 所追寻的那座城
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了机器学习笔记——Regression 1相关的知识，希望对你有一定的参考价值。
一、回归的主要应用场景
1、股市预测（Stock market forecast）
输入：过去10年股票的变动、新闻咨询、公司并购咨询等
输出：预测股市明天的平均值
2、自动驾驶（Self-driving Car）
输入：无人车上的各个sensor的数据，例如路况、测出的车距等
输出：方向盘的角度
3、商品推荐（Recommendation）
输入：商品A的特性，商品B的特性
输出：购买商品B的可能性
二、Regression的三个步骤
Step1 确定model
在regression中我们可以使用Linear Model(线性模型
y
=
b
+
w
⋅
x
\\mathrm{y}=\\mathrm{b}+\\mathrm{w} \\cdot \\mathrm{x}
y=b+w⋅x）
Function set:
y
=
b
+
Σ
w
i
X
i
{
X
i
:
an attribute of input
X
(
Features
)
ω
i
:
Weight of
X
i
b
: bias
y=b+\\Sigma w_{i} X_{i}\\left\\{\\begin{array}{l}X_{i}: \\text { an attribute of input } X(\\text { Features }) \\\\ \\omega_{i}: \\text { Weight of } X_{i} \\\\ b \\text { : bias }\\end{array}\\right.
y=b+ΣwiXi⎩⎨⎧Xi: an attribute of input X( Features )ωi: Weight of Xib : bias
step2 Goodness of function
Loss function — 衡量一组参数的好坏
L
(
f
)
=
L
(
w
,
b
)
=
∑
i
=
1
n
[
y
^
i
−
(
b
+
w
⋅
x
i
)
]
2
L(f)=L(w, b)=\\sum_{i=1}^{n}\\left[\\hat{y}^{i}-\\left(b+w \\cdot x^{i}\\right)\\right]^{2}
L(f)=L(w,b)=i=1∑n[y^i−(b+w⋅xi)]2
L
o
s
s
f
u
n
c
t
i
o
n
{
I
n
p
u
t
:
f
u
n
c
t
i
o
n
O
u
t
p
u
t
:
s
c
o
r
e
Loss function \\begin{cases} Input: function\\\\ Output: score \\end{cases}
Lossfunction{Input:functionOutput:score
Step3 Pick the best function
formulation:
{
f
∗
=
arg
min
f
(
f
)
w
∗
⋅
b
∗
=
arg
min
w
.
b
L
(
w
⋅
b
)
=
arg
min
w
,
b
∑
i
=
1
n
[
y
^
i
−
(
b
+
w
⋅
x
i
)
]
2
\\left\\{\\begin{array}{l}f^{*}=\\arg \\min _{f}(f) \\\\ \\left.w^{*} \\cdot b^{*}=\\arg \\min _{w . b} L(w \\cdot b)=\\arg \\min _{w, b} \\sum_{i=1}^{n} [ \\hat{y}^{i}-\\left(b+w \\cdot x^{i}\\right)\\right]^{2}\\end{array}\\right.
{f∗=argminf(f)w∗⋅b∗=argminw.bL(w⋅b)=argminw,b∑i=1n[y^i−(b+w⋅xi)]2
Parameter Description
x
i
{x}^{i}
xi:用上标来表示一个完整的object的编号(下标表示该object中的component)
y
^
i
\\hat{y}^{i}
y^i:用
y
^
i
\\hat{y}^{i}
y^i表示⼀个实际观察到的object输出，上标为i表示是第i个object
注：由于regression的输出值是scalar，因此 里面并没有component，只是⼀个简单的数值；但是未来如果考虑structured Learning的时候，我们output的object可能是有structured的，所以我们还是会需要用上标下标来表示⼀个完整的output的object和它包含的component
我们可以通过Gradient Desent（梯度下降）对其进行求解
只要
L
(
f
)
L(f)
L(f)是可微分的，gradient desent都可以对
f
f
f处理得到最佳的parameters
三、Gradient Desent（梯度下降算法）
1、单个参数
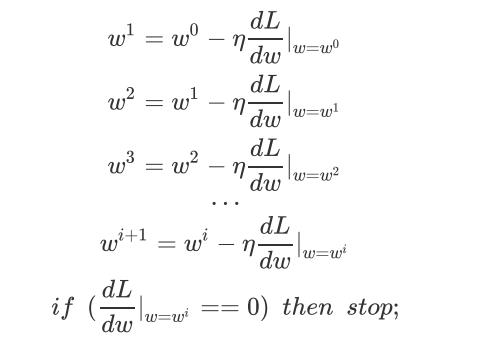
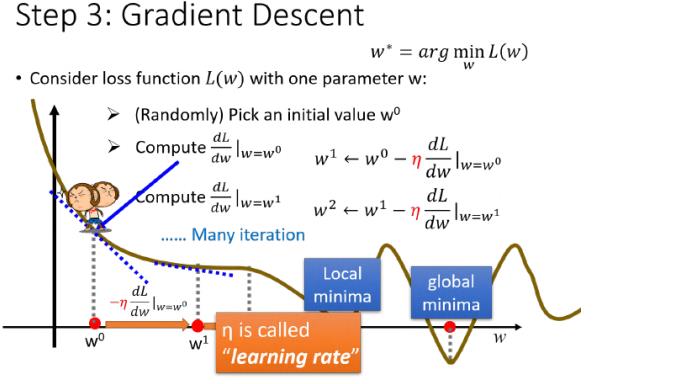
此时，
w
i
w_{i}
wi对应的斜率为0，找到local minima。因为local minima不一定为global minima，所以Gradient Desent找出来的并不一定为最优解。
但是我们并不需要担心这个问题，在linear regression中的loss function为凸函数，不存在local minima。所以我们找到的一定是global minima。
2、多个参数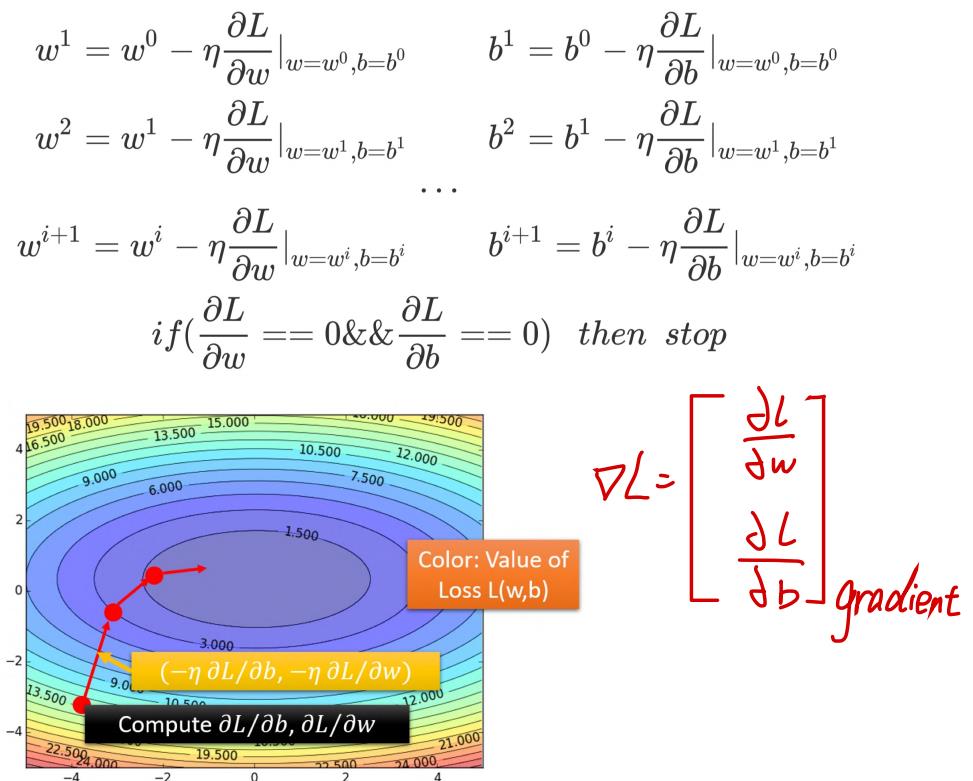
1、gradient为
∂
L
∂
w
\\frac{\\partial L}{\\partial w}
∂w∂L和
∂
L
∂
b
\\frac{\\partial L}{\\partial b}
∂b∂L组成的vector，该等高线的法线方向（图中红箭头的方向）
2、
(
−
η
∂
L
∂
b
,
−
η
∂
L
∂
w
)
\\left(-\\eta \\frac{\\partial L}{\\partial b},-\\eta \\frac{\\partial L}{\\partial w}\\right)
(−η∂b∂L,−η∂w∂L)的作用为：让原先的
(
ω
i
,
b
i
)
\\left(\\omega^{i}, b^{i}\\right)
(ωi,bi)朝着gradient的方向前进
3、
η
\\eta
η（learning rate）的作用为控制每次跨度
4、最终经过多次迭代，使得gradient达到最小点
四、How can we do better？
1、考虑更复杂的model
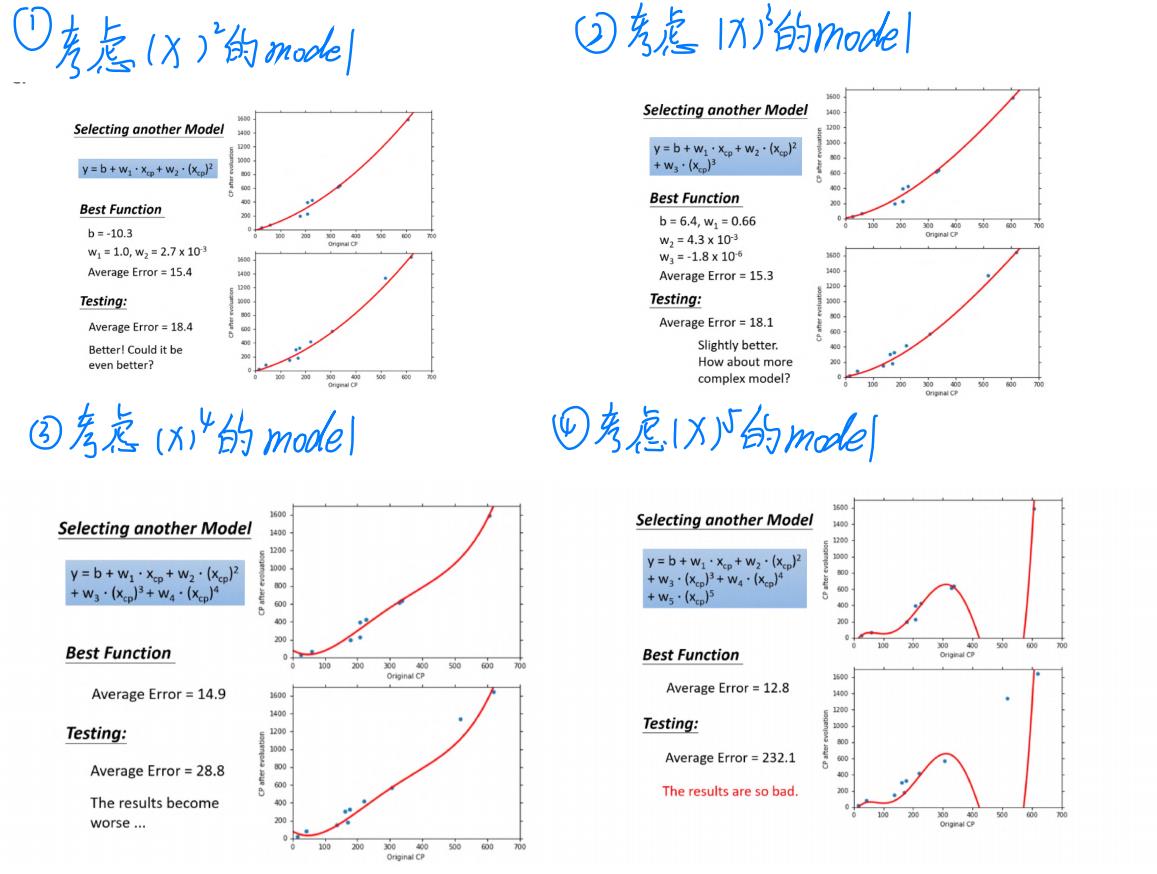由图中的结果我们可以发现：training data的error一定小于testing data，但是我们更加应该关心testing data的error。
在training data中：随着的高次项的增加，其Average Error就减小，但我们并不关心training data中的error。我们更关心model在testing data中的表现。
在testing data中：model复杂到一定的程度之后，error不但不减小，反而会暴增（over fitting现象）
因此，model并非是越复杂越好，我们需要找到一个合适的model
2、我们还可以考虑more features
重新设计model（已预测宝可梦的cp值为例）
Q : 我们能期望根据已有的宝可梦进化前后的信息，预测出某只宝可梦在进化后的cp大小。
若只考虑进化前后的cp，显然过于片面，我们可以加入物种这个feature
model: 以上是关于机器学习笔记——Regression 1的主要内容，如果未能解决你的问题，请参考以下文章 机器学习基石笔记-Lecture 10 Logistic regression 机器学习笔记-1 Linear Regression with Multiple Variables(week 2) 机器学习笔记（Washington University）- Regression Specialization-week four 机器学习笔记（Washington University）- Regression Specialization-week five 机器学习笔记（Washington University）- Regression Specialization-week six
If
x
s
=
x_{s}=
xs= Pidgey,
y
=
b
1
+
w
⋅
x
c
p
\\quad y=b_{1}+w \\cdot x_{c p}
y=b1+w⋅xcp
If
x
s
=
x_{s}=
xs= Weedle,
y
=
b
2
+
w
2
⋅
x
c
p
y=b_{2}+w_{2} \\cdot x_{c p}
y=b2+w2⋅xcp
If
x
s
=
x_{s}=