数据结构系列之Java手写实现红黑树
Posted smileNicky
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构系列之Java手写实现红黑树相关的知识,希望对你有一定的参考价值。
1、什么是红黑树?
在上一章的学习,我们知道了2-3-4树,其实2-3-4树和红黑树之前是可以相互转换的,红黑树是一种自平衡的二叉搜索树,是二叉搜索树的拓展。红黑树只有两种节点,一种是红色的,一种是黑色的。
红黑树不像AVL树那样严格,而是近似平衡。
所以一棵红黑树至少包含如下信息:
- left:左子节点
- right:右子节点
- data:数据存储在红黑树节点中
- color:节点颜色,红色或者黑色
static class RBNode<K extends Comparable<K> , V> {
private RBNode parent;
private RBNode left;
private RBNode right;
private boolean color;
private K k;
private V v;
public RBNode( K key, V value,RBNode parent) {
this.parent = parent;
this.k = key;
this.v = value;
}
}
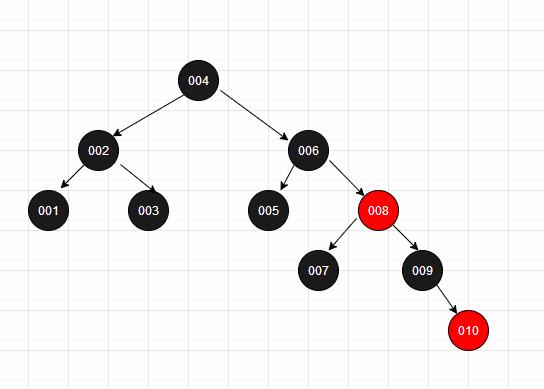
2、红黑树的特征
红黑树有如下特征,其目的是为了保证平衡
- 1、红黑树的根节点总是黑色的
- 2、树的节点总是红色或者黑色
- 3、每个叶子都是黑色的。如果一个节点不包含左右子节点,我们则将其子节点视为黑色的
- 4、如果一个节点是红色的,则其两个子节点都是黑色的
- 5、从根节点到叶子节点的每条路径都有相同数量的黑色节点
3、红黑树旋转操作
红黑树能自平衡,它靠的是什么?三种操作:左旋、右旋和变色
| 操作 | 描述 |
|---|---|
| 左旋 | 以某个节点作为旋转结点,其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。 |
| 右旋 | 以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变。 |
| 变色 | 结点的颜色由红变黑或由黑变红。 |
3.1、左旋操作
左旋:以某个节点作为旋转点,其右子节点变为旋转节点的父节点,右子节点的左子节点变为旋转节点的右子节点,左子节点保持不变。
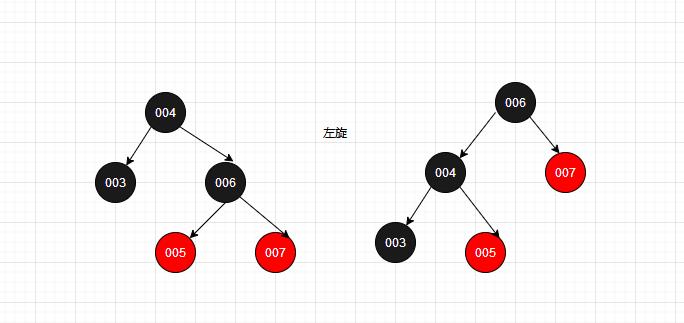
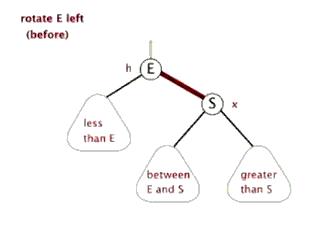
网上很多地方都有这种gif图片,原文不知道来自哪里,暂且借来做说明:
java实现红黑树左旋逻辑:
左旋算法分步进行:
- 1、将pr节点的左子节点更新为p的右子节点,pr有左子节点时,将p赋给pr左子节点rl的父节点
- 2、 p有父节点r时,将p的父节点赋给pr的父节点,同时更新r的左子节点或者右子节点为pr
- 3、将pr的左子节点设为p,将p的父节点设为pr
/**
* 左旋示意图:围绕p进行左旋
* r r
* / /
* p pr
* / \\ / \\
* pl pr => p rr
* / \\ / \\
* rl rr pl rl
* 左旋算法分步进行:
* 1. 将pr节点的左子节点更新为p的右子节点,pr有左子节点时,将p赋给pr左子节点rl的父节点
* 2. p有父节点r时,将p的父节点赋给pr的父节点,同时更新r的左子节点或者右子节点为pr
* 3. 将pr的左子节点设为p,将p的父节点设为pr
* @param
*/
private void leftRotate(RBNode p) {
if(p != null) {
// 1. 将pr节点的左子节点更新为p的右子节点,pr有左子节点时,将p赋给pr左子节点rl的父节点
// 获取pr节点,也即为p的右节点
RBNode pr = p.right;
// 将pr节点的左子节点更新为p的右子节点
p.right = pr.left;
//pr有左子节点时,将p赋给pr左子节点rl的父节点
if (pr.left != null) {
pr.left.parent = p;
}
// 2. p有父节点r时,将p的父节点赋给pr的父节点,同时更新r的左子节点或者右子节点为pr
// 不管p是否存在父节点,我们都设置p的父节点也为 pr的父节点
pr.parent = p.parent;
if (p.parent == null) {
// 直接设置root节点为pr
this.root = pr;
} else {
// 有r根节点的情况
if (p == p.parent.left) {
// 原来的p节点为r的左节点的情况
p.parent.left = pr;
} else {
// 原来的p节点为r的右节点的情况
p.parent.right = pr;
}
}
// 3. 将pr的左子节点设为p,将p的父节点设为pr
pr.left = p;
p.parent = pr;
}
}
3.2、右旋操作
右旋:以某个节点作为旋转点,其左子节点变为旋转节点的父节点,左子节点的右子节点变为旋转节点的左子节点,右子节点保持不变
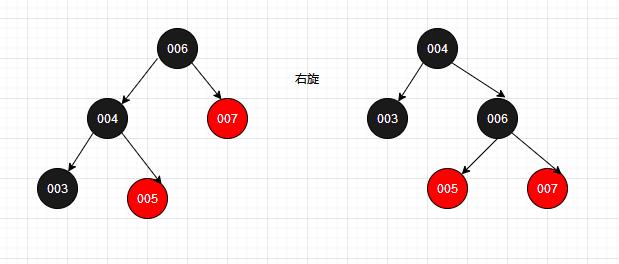
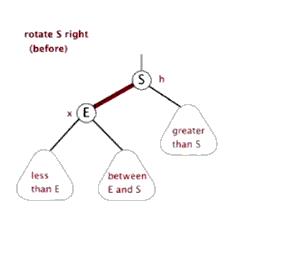
右旋算法分步进行:
- 1、 将pl节点的右子节点更新为p的左子节点,pl有右子节点时,将p赋给pl右子节点rr的父节点
- 2、p有父节点r时,将p的父节点赋给pl的父节点,同时更新r的左子节点或者右子节点为pl
- 3、将pl的右子节点设为p,将p的父节点设为pl
java实现红黑树右旋:
/**
* 右旋示意图:围绕p进行右旋
* r r
* / /
* p pl
* / \\ / \\
* pl pr => rl p
* / \\ / \\
* rl rr rr pr
* 右旋算法分步进行:
* 1. 将pl节点的右子节点更新为p的左子节点,pl有右子节点时,将p赋给pl右子节点rr的父节点
* 2. p有父节点r时,将p的父节点赋给pl的父节点,同时更新r的左子节点或者右子节点为pl
* 3. 将pl的右子节点设为p,将p的父节点设为pl
* @param
*/
public void rightRotate(RBNode p) {
if(p != null) {
// 1. 将pl节点的右子节点更新为p的左子节点,pl有右子节点时,将p赋给pl右子节点rr的父节点
// 获取pl节点,也即为p的左节点
RBNode pl = p.left;
// 将pl节点的右子节点更新为p的左子节点
p.left = pl.right;
//pl有右子节点时,将p赋给pl右子节点rl的父节点
if (pl.right != null) {
pl.right.parent = p;
}
// 2. p有父节点r时,将p的父节点赋给pl的父节点,同时更新r的左子节点或者右子节点为pl
pl.parent = p.parent;
if (p.parent == null) {
// 直接设置root节点为pr
this.root = pl;
} else {
// 有r根节点的情况
if (p == p.parent.right) {
// 原来的p节点为r的右节点的情况
p.parent.right = pl;
} else {
// 原来的p节点为r的左节点的情况
p.parent.right = pl;
}
}
// 3. 将pl的右子节点设为p,将p的父节点设为pl
pl.right = p;
p.parent = pl;
}
}
4、红黑树新增节点
红黑树是一棵二叉搜索树,所以新增逻辑也可以类似的,如下代码,这个逻辑就是和二叉搜索树的新增节点是一样的,就是一个节点一个节点做比较大小,然后找到一个节点作为新节点的父节点,然后再判断是要做左子节点,还是右子节点就可以
/**
* 新增红黑树节点操作 . <br>
* @Date 2021/08/12 16:31
* @Param [key, value]
* @return void
*/
public void put(K key, V value) {
RBNode<K,V> parent = null ;
RBNode<K,V> t = root;
// 找不到root节点,将新节点作为root节点
if (t == null) {
root = new RBNode<>(key, value, parent);
return;
}
// 找到节点作为新增节点的父节点
while (t != null) {
parent = t;
int cmp = key.compareTo(t.k);
if (cmp < 0) {
t = t.left;
} else {
t = t.right;
}
}
// 创建新节点,判断新节点是作为parent节点的左节点还是右节点
RBNode<K,V> node = new RBNode<K, V>(key , value , parent);
int comp = node.k.compareTo(parent.k);
if (comp < 0) {
parent.left = node;
} else {
parent.right = node;
}
// 关键,新增节点之后,红黑树的调整
fixAfterInsertion(node);
}
红黑树的新增,前面逻辑是和二叉搜索树一样的,不同的是新增节点后,为了保证平衡,需要做旋转和变色操作,具体逻辑看一下fixAfterInsertion(node);,这个逻辑比较关键,这里做一下比较详细的描述,这里分情况分析
-
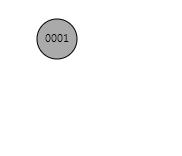
场景1: 红黑树是Empty的,这是最简单的场景,直接将新节点作为根节点就行,不过红黑树有个特性,根节点都是黑色的,所以将新节点涂黑就行
-
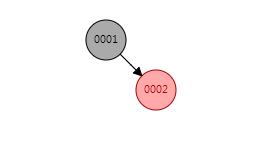
场景2:新增节点的父节点是黑节点,由于新增的节点都是红色的节点,所以这种情况不会影响平衡,直接新增就行
-
场景3:新增结点的父结点为红结点且为祖父节点的左子节点
-
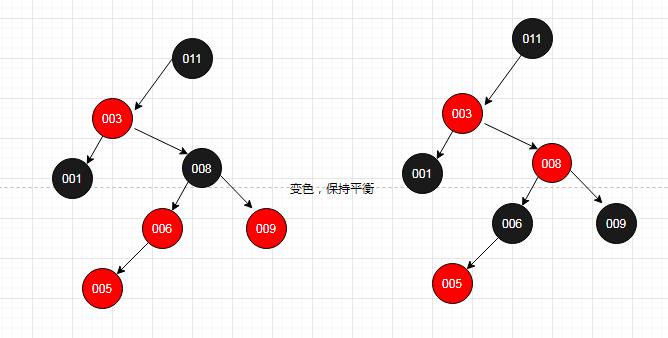
场景3.1:新节点的叔叔节点是红色的
这种情况,如图005是新增节点,其叔叔节点是009是红色的,这种情况,需要做下变色,祖父节点008变为红色,父亲节点006变为黑色,叔叔节点009也变为黑色,这样整棵红黑色就可以平衡
-
场景3.2:叔叔节点是黑色,且新增节点作为右子节点
这种情况要做的是将新节点008指向父节点003,同时做左旋
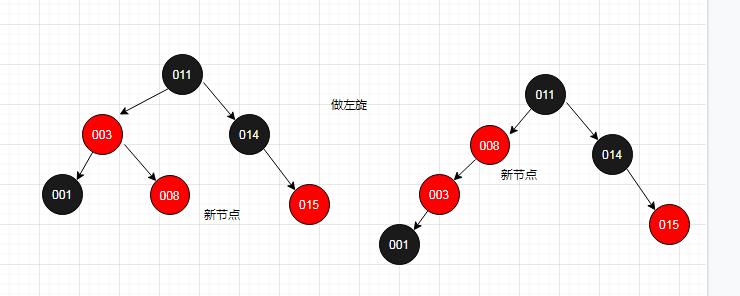
-
场景3.3:叔叔节点是黑色,且新增节点作为左子节点
这种情况,需要将父节点008变黑色,祖父节点011变为红色,同时围绕祖父节点011做右旋
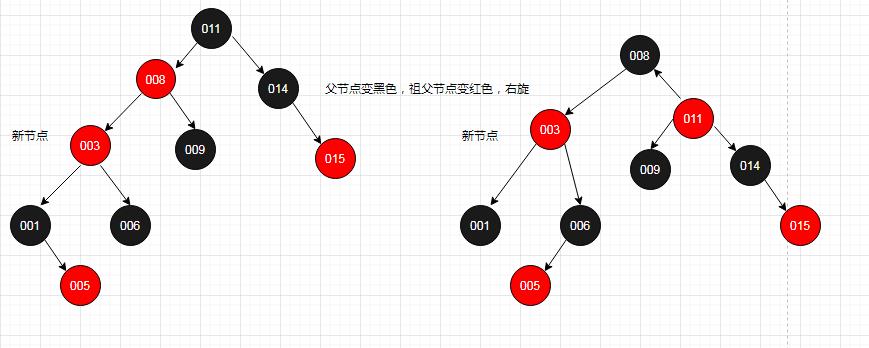
-
-
场景4:新增结点的父结点为红结点,且为祖父节点的右子节点
这种场景也有3种情况,不过和场景3是相反的,这种不做详细描述
/**
* 新增节点之后,红黑树的调整操作 <br>
* @Date 2021/08/12 17:36
* @Param [node]
* @return void
*/
private void fixAfterInsertion( RBNode<K,V> node) {
node.color = RED;
// 父节点是红色的,才需要调整,黑色节点直接新增就行
while (node != null && node != root && node.parent.color == RED) {
// 父节点是祖父节点的左节点
if (parentOf(node) == leftOf(parentOf(parentOf(node)))) {
// 找到叔叔节点
RBNode<K,V> y = rightOf(parentOf(parentOf(node)));
// case1 : 叔叔节点也是红色
if (y != null && colorOf(y) == RED) {
setColor(parentOf(node) , BLACK);
setColor(y , BLACK);
setColor(parentOf(parentOf(node)) , RED);
node = parentOf(parentOf(node));
}
else {
// case2 : 叔叔节点是黑色,且新增节点是右子节点
if (node == rightOf(parentOf(node))) {
// 将父节点和新增节点调换
node = parentOf(node);
// 从父节点处做左旋
leftRotate(node);
}
// case 3 : 叔叔节点是黑色,且新增节点是左子节点
setColor(parentOf(node) , BLACK);
setColor(parentOf(parentOf(node)) , RED);
rightRotate(parentOf(parentOf(node)));
}
}
else {
// 找到叔叔节点
RBNode<K,V> y = leftOf(parentOf(parentOf(node)));
// case1 : 叔叔节点也是红色
if (y != null && colorOf(y) == RED) {
setColor(parentOf(node) , BLACK);
setColor(y , BLACK);
setColor(parentOf(parentOf(node)) , RED);
node = parentOf(parentOf(node));
}
else {
// case2 : 叔叔节点是黑色,且新增节点是左子节点
if (node == leftOf(parentOf(node))) {
node = parentOf(node);
rightRotate(node);
}
// case 3 : 叔叔节点是黑色,且新增节点是右子节点
setColor(parentOf(node) , BLACK);
setColor(parentOf(parentOf(node)) , RED);
leftRotate(parentOf(parentOf(node)));
}
}
}
// root节点肯定是黑色
root.color = BLACK;
}
测试代码:
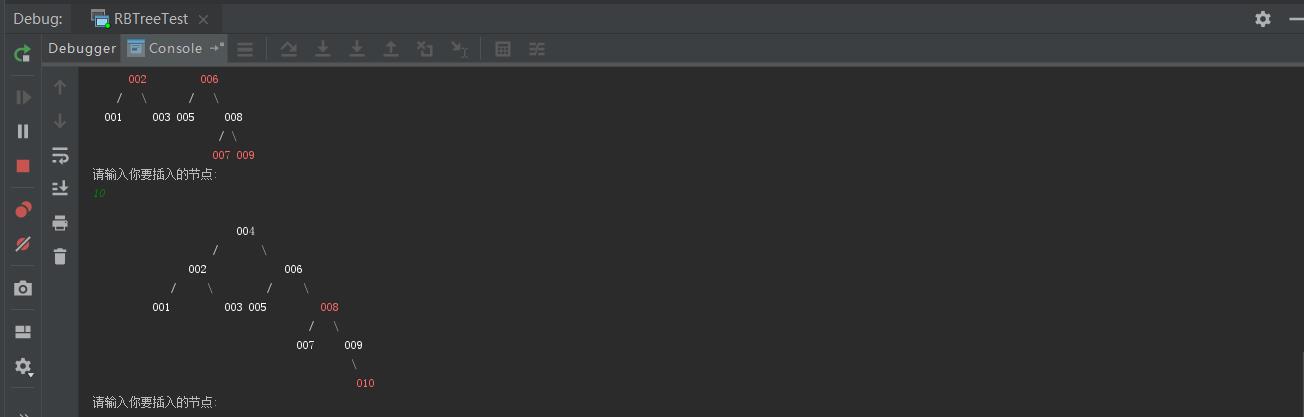
使用在线网站进行验证:
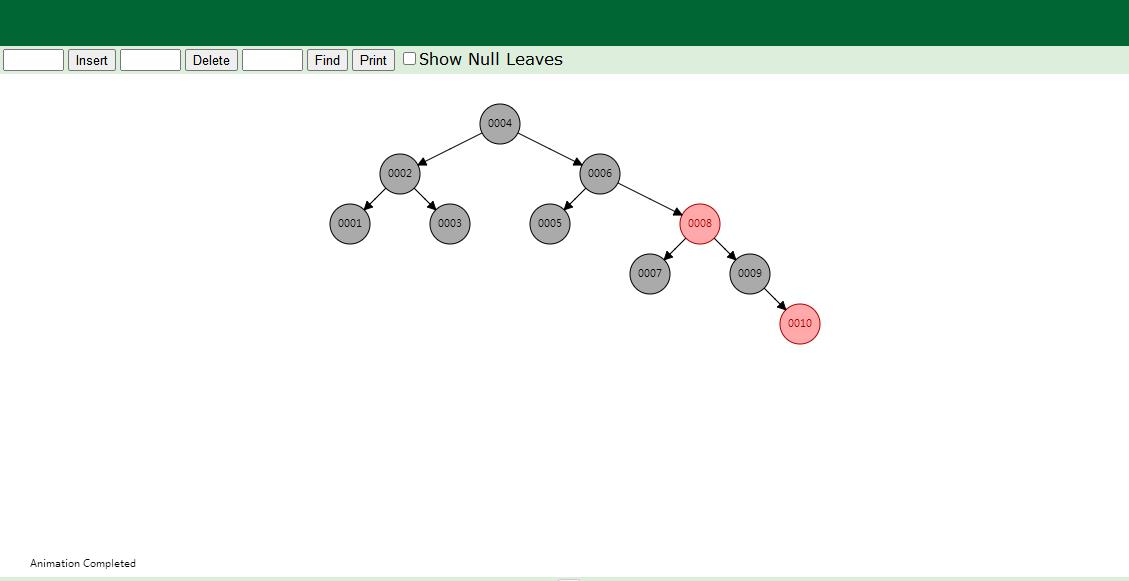
5、红黑树移除节点
前期准备,找到对应节点:
/**
* 根据key移除节点 <br>
* @Date 2021/08/13 10:28
* @Param [key]
* @return V
*/
public V remove(K key){
// 1. 根据需要删除的key 找到对应的Node节点
RBNode node = getNode(key);
if(node == null){
// 不存在
return null;
}
V oldValue = (V) node.v;
// 具体删除节点的方法
deleteEntry(node);
return oldValue;
}
/**
* 根据key找到对应node <br>
* @Date 2021/08/13 10:29
* @Param [key]
* @return com.example.datastructure.rbtree.RBTree.RBNode
*/
private RBNode getNode(K key) {
RBNode node = this.root;
while(node != null){
int cmp = key.compareTo((K) node.k);
if(cmp < 0){
node = node.left;
}else if(cmp > 0){
node = node.right;
}else{
// 表示找到了对应的节点
return node;
}
}
return null;
}
红黑色的删除操作和二叉树前半部分是一样的,
有三种情况:
- 1:删除叶子节点,直接删除
- 2:删除有一个子节点的情况,找到替换节点
- 3:如果删除的节点右两个子节点,此时需要找到前驱节点或者后继节点
/**
* 删除节点操作. <br>
* 有三种情况:
* 1:删除叶子节点,直接删除
* 2:删除有一个子节点的情况,找到替换节点
* 3:如果删除的节点右两个子节点,此时需要找到前驱节点或者后继节点
* @Date 2021/08/12 17:35
* @Param [node]
* @return void
*/
public void deleteEntry(RBNode<K,V> node) {
// 3、node节点有两个子节点的情况,找到前驱节点,复制前驱节点的元素给node节点,同时改变指针
if (node.left != null && node.right != null) {
RBNode<K,V> s = predecessor(node);
node.k = s.k;
node.v = s.v;
node = s;
}
// 2、删除有一个子节点的情况找到替换节点
RBNode<K,V> replacement = node.left != null? node.left : node.right;
if (replacement != null) {
// 改变指针
replacement.parent = node.parent;
if (node.parent == null ){
// node是root节点
root = replacement;
}
else if (node == node.parent.left){
// 替换为左节点
node.parent.left = replacement;
}
else {
// 替换为右节点
node.parent.right = replacement;
}
// 指针都指向null,等待GC
node.left = node.right = node.parent = null;
// 红黑树平衡
if (node.color == BLACK) {
fixAfterDeletion(replacement);
}
}
else if (node.parent == null) {
// 说明要删除的是root节点
root = null;
}
else {
// 1、node节点是叶子节点
// 先调整
if (node.color == BLACK) {
fixAfterDeletion(node);
}
// 再删除
if (node.parent != null) {
if (node == node.parent.left) {
node.parent.left = null;
} else if (node == node.parent.right) {
node.parent.right = null;
}
node.parent = null;
}
}
}
查找后继节点,后继节点就是先定位到右节点,然后一直往左查找,找到最小值
/**
* 查找后继节点,后继节点就是先定位到右节点,然后一直往左查找,找到最小值<br>
* @Author mazq
* @Date 2021/08/12 17:17
* @Param [node]
* @return com.example.datastructure.rbtree.RBTree.RBNode<K,V>
*/
private RBNode<K , V> successor(RBNode<K , V> node) {
if (node == null) {
return null;
} else if (node.right != null) {
// 取到右节点
RBNode<K , V> p = node.right;
// 往左查找,找到最小值
while(p.left != null) {
p = p.left;
}
return p;
} else {
// 比较少见的情况,该节点没有右子节点,往上遍历
RBNode<K ,V> p = node.parent;
RBNode<K , V> ch = node;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}
前驱节点,定位到左节点,一直找右找,找到最大值
/**
* 查找前驱节点 <br>
* @Author mazq
* @Date 2021/08/12 17:17
* @Param [node]
* @return com.example.datastructure.rbtree.RBTree.RBNode<K,V>
*/
private RBNode<K , V> predecessor(RBNode<K , V> node) {
if (node == null) {
return null;
} else if (node