SDUT 2021 Summer Individual Contest - 7（补题）

Posted 2021-09-06 佐鼬Jun

E - Charles in Charge

题意： 一个人用电瓶车在公路上骑行，每到一个点都可以充电，电有多少就能跑多少里路，现在要求你在跑的路程在不超过最短路径的X%的情况下，电动车的电池容量越小越好，问你电动车的最小容量是多少。
思路： 先跑一遍最短路求出正常的最短路，然后二分求电车的电池容量，即公路的长度，在二分的处理最短路的时候，本来要把大于电池容量的公路删掉，但不好操作，所以直接在$Dijkstra$中，对于那些大于电池容量的公路直接不操作，当作没有这条边即可。

#include <bits/stdc++.h>
using namespace std;
#define inf 0x7f7f7f7f3f3f3f3f
#define int long long
const int N = 1e4 + 10, M = 2e5 + 10;
typedef pair<int, int> PII;
#define ll long long
bool vis[N];
int dis[N];
int h[N], w[M], e[M], ne[M], idx;
int n, m, x;
ll dex;
void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

int dijkstra(int mid) {
    memset(dis, 0x7f, sizeof(dis));
    memset(vis, 0, sizeof(vis));
    dis[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII> > q;
    q.push({0, 1});
    while (q.size()) {
        auto t = q.top();
        q.pop();
        int now = t.second;
        int distance = t.first;
        if (vis[now]) continue;
        vis[now] = 1;
        for (int i = h[now]; i != -1; i = ne[i]) {
            int j = e[i];
            if (w[i] > mid) {
                continue;
            }
            if (dis[j] > dis[now] + w[i]) {
                dis[j] = dis[now] + w[i];
                q.push({dis[j], j});
            }
        }
    }
    return dis[n];
}
signed main() {
    memset(h, -1, sizeof(h));
    cin >> n >> m >> x;
    while (m--) {
        int a, b, c;
        scanf("%lld%lld%lld", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }
    dex = (ll)dijkstra(inf);
    dex = dex + dex * x / 100;
    int l = 0, r = dex + 1;
    while (l < r) {
        int mid = (l + r) / 2;
        if ((ll)dijkstra(mid) <= dex) {
            r = mid;
        } else {
            l = mid + 1;
        }
    }
    cout << l << endl;
}

D - Bridge Automation

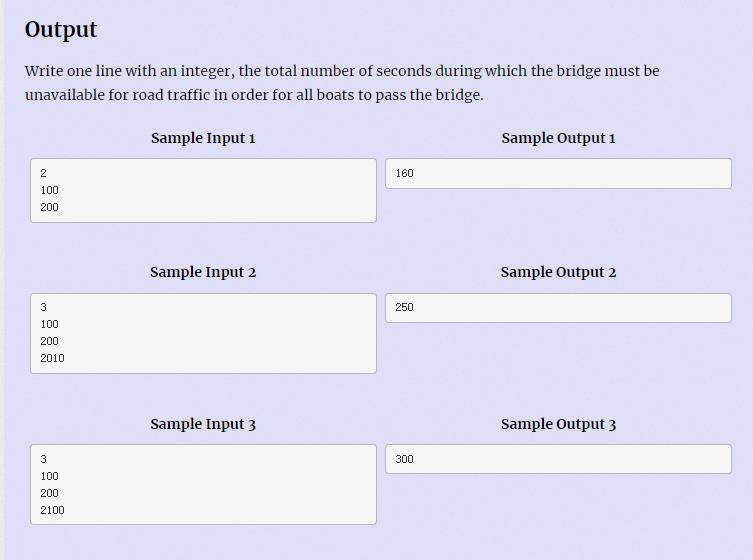
题意： 有个桥升起和下降都需要60秒，船穿过桥需要20秒，一个船在桥前最多等待30min，只有当完全升起的时候，船才能过去，如果在桥前有多个船在等待，那也需要一个一个过去，现在给每个船的到达时间，现在问最少保持抬起状态多长时间(升起和下降的过程也算)
思路： 设立$f(i)$为到$i$个船为止，桥保持抬起状态的时间。
一.第$i-1$个没等它，第$i$个船到的时候，是走完了升起和下降和过桥的全流程也就是$f(i-1)+60+60+20$
二.前面有船等它，设立这个等它的船为第j号船，那么此时又有两种情况.
1、第j号船等不下去，等了30分钟了后，就开走了，等的这30分钟桥是在我完全下降状态，但是桥仍保持这完全升起状态，所以就是$f[j-1]+a[i]-a[j]-1800+20+120$
2.第j号船能等下去，就一直等第i号船，也就是$f[j-1]+(i-j+1)\cdot 20+120$

#include <bits/stdc++.h>
using namespace std;
const int N = 4444;
int a[N], f[N];
int n;
int main() {
    ios_base::sync_with_stdio(false);
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    for (int i = 1; i <= n; i++) {
        f[i] = f[i - 1] + 140;
        for (int j = 1; j < i; j++) {
            f[i] = min(f[i], f[j - 1] + max((a[i] - a[j] - 1800) + 20 + 120, (i - j + 1) * 20 + 120));
        }
    }
    cout << f[n] << endl;
    return 0;
}

J - Programming Tutors

题意： 给n个学生和n个教练的平面坐标，他们之间的距离是曼哈顿距离，使学生和教练之间两两匹配，使得他们匹配的之间匹配的最大距离最小
思路： 二分+匈牙利，二分他们之间匹配的最大距离，如果小于正确答案res，那肯定不能两两匹配，如果大于一定是可以两两匹配的，但距离可以再缩小，在二分图中匹配时，就用mid来作为边界，距离大于mid的双方不能匹配，最后看能否一一匹配。

#include <bits/stdc++.h>
using namespace std;
const int N = 222;
#define ll long long
struct node {
    ll x, y;
} a[N], b[N];
ll g[N][N];
int vis[N];
int match[N];
int n;
bool find(int u, ll mid) {
    for (int i = 0; i < n; i++) {
        if (g[u][i] <= mid && !vis[i]) {
            vis[i] = 1;
            if (match[i] == -1 || find(match[i], mid)) {
                match[i] = u;
                return 1;
            }
        }
    }
    return 0;
}
bool check(ll mid) {
    int res = 0;
    for (int i = 0; i < n; i++) {
        memset(vis, 0, sizeof(vis));
        if (find(i, mid)) res++;
    }
    if (res == n)
        return 1;
    else
        return 0;
}
int main() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> a[i].x >> a[i].y;
    }
    for (int i = 0; i < n; i++) {
        cin >> b[i].x >> b[i].y;
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            g[i][j] = abs(a[i].x - b[j].x) + abs(a[i].y - b[j].y);
        }
    }
    ll l = 0, r = 1e12;
    while (l < r) {
        memset(match, -1, sizeof(match));
        ll mid = (l + r) / 2;
        if (check(mid))
            r = mid;
        else
            l = mid + 1;
    }
    cout << l << endl;
    return 0;
}

To be continued
如果你有任何建议或者批评和补充，请留言指出，不胜感激