故障诊断基于PSO_VMD_MCKD方法的风机轴承微弱故障诊断

Posted 2021-09-06 Zhi Zhao

目录

• 一、基本理论
• • 1. PSO算法
  • 2. VMD算法
  • 3. MCKD算法
  • • 3.1 算法简介
    • 3.2 算法原理
• 二、PSO_VMD_MCKD
• 三、MATLAB代码
• 参考文献

一、基本理论

1. PSO算法

有关PSO的介绍请阅读博文：PSO-LSSVM算法及其MATLAB代码

2. VMD算法

有关VMD的介绍请阅读博文：VMD算法

3. MCKD算法

3.1 算法简介

最大相关峭度解卷积（Maximum Correlated Kurtosis Deconvolution，简称MCKD）通过解卷积运算突出被噪声淹没的连续脉冲，提高原始信号的相关峭度值，适用于提取微弱故障信号的连续瞬态冲击。

3.2 算法原理

MCKD算法的实质是寻找一个FIR滤波器来恢复被噪声淹没的连续冲击信号，而为了验证该滤波器恢复出的信号是否满足周期性冲击特性，需要利用相关峭度指标来衡量。相关峭度定义为：
$$C{K}_M(T)=\frac{{\sum }_{n=1}^N({\prod }_{m=0}^M{y}_n-mT{)}^2}{({\sum }_{i=1}^N{y}_n^2{)}^{M+1}}$$
其中，$T$为冲击信号周期；$M$为移位数；$m\in [0，M]$；$L为滤波器的长度$；$y_n$为冲击信号。
对信号进行滤波，当相关峭度$C{K}_M(T)$最大时，求解出来的滤波器就是满足要求的。假设输入信号为$x$，输出信号为$y$，FIR滤波器对信号进行滤波的原理如下：
$$y=f\ast x$$
求解上式中的滤波器系数 $f$ ，就是解卷积运算的过程。

二、PSO_VMD_MCKD

为实现 VMD 和 MCKD 的参数自适应选择，采用粒子群优化算法对两种算法中的参数进行优化，确定适应度函数为包络谱峰值因子。
方法流程：
1）设定VMD的模态数 K 和惩罚因子 alpha 的寻优范围，利用PSO对VMD算法进行参数寻优；
2）得到VMD的最优模态数 Best_K 和最优惩罚因子 Best_alpha ，再利用VMD对原始信号进行分解，计算各分量的包络谱峰值因子 Ec，选择 Ec 指标最大的分量为最优分量；
3）设定MCKD的滤波器长度参数 L 和 解卷积周期T的寻优范围，利用PSO对VMD算法进行参数寻优；
4）得到MCKD的最优滤波器长度参数 Best_L 和 最优解卷积周期Best_T，再对最优分量进行MCKD分析，最后对解卷积后的信号进行包络解调。

三、MATLAB代码

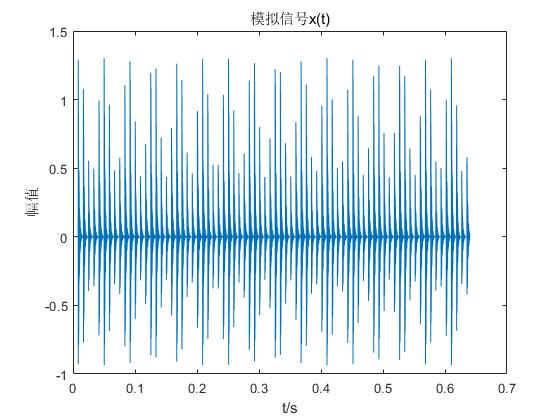
Simulating_faultSignal.m：产生仿真信号

clc;
clear;
close all;
%% 仿真信号
A0 = 0.5;       % 位移常数
fr = 25;        % 转频
C = 800;        % 衰减系数 
fn = 4e3;       % 共振频率
T = 1/120;      % 重复周期
fs = 12800;     % 采样频率
N = 8192;       % 采样点数
SNR = -16;      % 信噪比
NT = round(fs*T);       % 单周期采样点数
t0 = (0:NT-1)/fs;       % 单周期采样时间
t = (0:N-1)/fs;         % 采样时间
k = ceil(N/NT)-1;      % 重复次数

x = [];
% 产生k个相同波形
for i = 1:k
      t1 = ((i-1)*NT)/fs:1/fs:(i*NT-1)/fs;      % k个周期
      Ak = A0*sin(2*pi*fr*t1)+1;
      h = exp(-C*t0).*sin(2*pi*fn*t0);
      x = [x,Ak .* h];
end
tt0 = 0:1/fs:((N/NT-k)*NT)/fs;        % k个周期后剩下的采样时刻
tt1 = k*NT/fs:1/fs:(N-1)/fs;
x = [x,((A0*sin(2*pi*fr*tt1)+1).*exp(-C*tt0).*sin(2*pi*fn*tt0))];
x(1:NT) = 0;    % 第一个单周期内的信号幅值为0
nt = wgn(1,N,-16);  % 高斯白噪声
y = x + nt;

PSO_VMD.m：PSO优化VMD（非完整代码）

%% PSO优化VMD
load y;               % y为含噪声信号
P_number = 30;        % 粒子群个数
C1 = 2;               % 初始化学习因子
C2 = 2;
W_max = 0.90;           % 初始权重
W_min = 0.4;            % 终止权重
iter = 20;                  % 迭代次数

% 定义优化参数的取值范围：K取[3,10]，Alpha取[100,2000]
Kmax = 10;        % 定义优化参数的取值范围
Kmin = 3;
Alphamax = 2000;
Alphamin = 100;

% 定义适应度函数
function f = Adaptness1(K,alpha,y)

    K=round(K);
    alpha=round(alpha);
    % VMD分解
    % x：为待分解的时域信号
    % u：分解模式的集合
    % u_hat：模式的频谱
    % omega：估计模式中心频率
    % K：分解的模态数
    % alpha：惩罚因子，也称平衡参数
    tau = 0;            % 噪声容忍度
    DC = 0;             % 无直流分量
    init = 1;           % 初始化中心频率为均匀分布
    tol = 1e-7;         % 收敛准则容忍度
    [u, ~, omega] = VMD(y, alpha, tau, K, DC, init, tol);

Best_VMD.m（非完整代码）：利用VMD对含噪声信号进行分解，得到最优分量

%% 利用PSO优化VMD得到的最优参数，再进行VMD分解
load y;               % y为含噪声信号
load bestK;
load bestAlpha;

% VMD分解
% x：为待分解的时域信号
% u：分解模式的集合
% u_hat：模式的频谱
% omega：估计模式中心频率
% K：分解的模态数
% alpha：惩罚因子，也称平衡参数
tau = 0;            % 噪声容忍度
DC = 0;             % 无直流分量
init = 1;           % 初始化中心频率为均匀分布
tol = 1e-7;         % 收敛准则容忍度
[u, ~, omega] = VMD(y, bestAlpha, tau, bestK, DC, init, tol);

PSO_MCKD.m：PSO优化MCKD（非完整代码）

%% PSO优化MCKD
load X1;     % 读取最优分量
y = X1;
P_number = 30;        % 粒子群个数
C1 = 2;               % 初始化学习因子
C2 = 2;
W_max = 0.90;           % 初始权重
W_min = 0.4;            % 终止权重
iter = 20;                  % 迭代次数

% 定义优化参数的取值范围：L取[100,1000]，T取[90,150]
Lmax = 1000;        % 定义优化参数的取值范围
Lmin = 100;
Tmax = 142;
Tmin = 85;

% 定义适应度函数
function Ad = Adaptness2(filterSize,T,y)

    filterSize = round(filterSize);
    T = round(T);
    termIter = 30;
    M = 3;
    plotMode = 0;
    [y_final, ~, ~] = MCKD(y,filterSize,termIter,T,M,plotMode);

Best_MKCD.m（非完整代码）：利用MCKD对最优分量进行解卷积得到最终的信号 y_final

%% 利用PSO优化MCKD得到的最优参数，再进行MCKD分析
load X1;     % 读取最优分量
load bestL;
load bestT;

% MCKD：最大相关峭度解卷积
termIter = 30;
M = 3;
plotMode = 0;
[y_final, f_final, ckIter] = MCKD(X1,bestL,termIter,bestT,M,plotMode);

求信号的频谱和包络谱的函数

% 求信号的频谱
[f1,A] = PinPu(y,fs);

% 求信号的包络谱
[f2,EnvA1] = Envelope(y,fs);

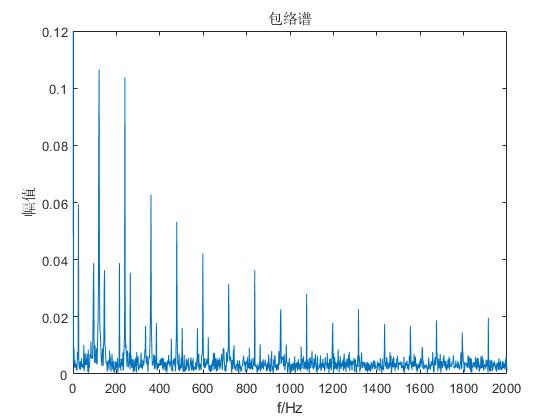
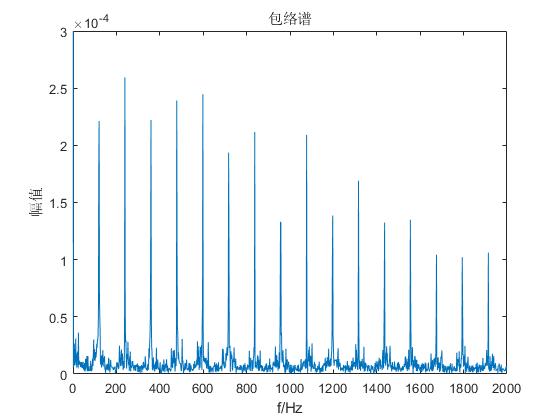
完整的MATLAB代码地址如下：

PSO_VMD_MCKD

参考文献

张俊, 张建群, 钟敏, 等. 基于PSO_VMD_MCKD方法的风机轴承微弱故障诊断[J]. 振动、测试与诊断, 2020,40(2):287-290.