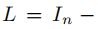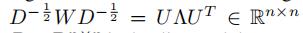交通预测论文笔记：Spatio-Temporal Graph Convolutional Networks: A Deep Learning Frameworkfor Traffic Forecast

Posted 2021-09-06 UQI-LIUWJ

0 abstract

        由于交通数据极强的非线性和复杂性，传统方法很难进行中长期的交通预测。

        我们提出了STGCN结构来解决交通领域的预测问题。我们的模型建立在卷积之上，有更快的训练速度和更少的参数。

1 introduction

        交通预测问题，根据预测时间片的长度，可以分为：短期（5~30分钟）和长期（30分钟以上）。大部分统计方法在短期预测上效果很好，但是因为交通流数据的不确定性和复杂性，这些模型在长期预测上效果很一般。

        早期关于中长期交通预测的研究主要集中在动态建模和数据驱动的方法上。

        数据建模：

        使用数学工具（比如微分方程）和物理知识来模拟交通场景，解决交通问题

        但这需要复杂的系统化的编程，还需要大量的算力。

        同时，不切实际的假设和简化很有可能会使得预测的精准度不足

        因此，随着交通数据收集和存储技术的进步，越来越多的研究侧重于数据驱动

         数据驱动：

        又分为传统统计学方法和机器学习方法

        在时间序列分析问题里面，ARIMA和它的变体是很经典的一类方法。但是这种模型受限于对于时间序列平稳性的假设，同时它没有把时空相关性纳入考虑范围。因此，这种方法没法解决高度非线性的交通流量预测问题。

        机器学习方法有KNN,SVM,NN等

        深度学习方法

        深度信念网络DBN、迭代自动编码器SAE都曾用作交通预测，但是，这些模型都无法同时提取交通数据的时间和空间特征。

        之后出现了CNN+RNN的模型来同时考虑时间和空间特征，但是这些模型只能处理网格化交通路网（现实生活中网格状路网是很少，甚至没有的），同时RNN还有误差累积以及训练较慢、较难计算的问题。

        为了解决这一问题，本文提出了使用ＧＮＮ代替ＣＮＮ，使用卷积代替ＲＮＮ的想法来建立一个完全由卷积组成的神经网络。

２　Preliminary

 2.1 图上的交通预测

        根据之前的M个时刻的交通观测数据，预测之后H个时刻的交通数据：

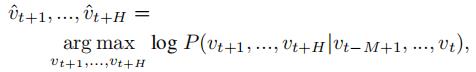
其中 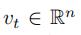表示t时刻，n个交通观测点的观测结果

 

我们记交通网络图为：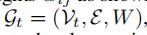 

其中，Y表示时刻t的节点集合，ε是边集合，W代表加权的邻接矩阵

2.2 谱图卷积

谱图卷积通过图傅里叶变换将卷积操作变换到谱域内进行操作。

我们记*g为谱图卷积算子，Θ为谱图卷积核，那么我们有：

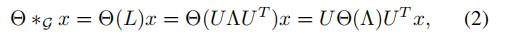
其中 标准化拉普拉斯矩阵

        In是单位矩阵

        ​是度矩阵，

         是L的特征值组成的对角矩阵

         傅里叶基是标准化拉普拉斯矩阵L的特征向量组成的矩阵

        在谱域上的图卷积核也是一个对角矩阵 

3 模型结构         

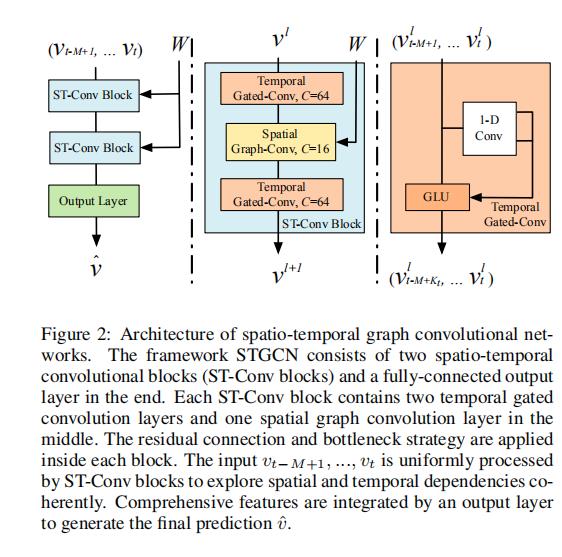
STGCN 有多个时空卷积块组成，每一个是一个三明治结构，由两层序列卷积层和一层空间图卷积层组成

 

3.1 提取空间特征的图卷积 

3.1.1 切比雪夫多项式近似

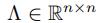我们用关于的多项式来近似图卷积核Θ，其中 是L的特征值组成的对角矩阵

 、

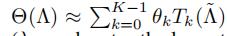其中：K表示距离中心节点最远的卷积范围

           （λmax表示拉普拉斯矩阵L最大的特征值 ）

 于是，切比雪夫多项式近似的图卷积可以写成：

 

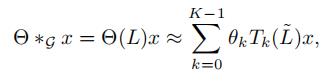
其中 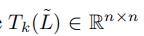表示关于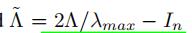的k阶切比雪夫多项式

 

通过切比雪夫多项式的近似，谱图卷积的复杂度可以降低到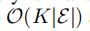（ε是边集合）

3.1.2 一阶近似

        一个层级的线性方程可以由堆叠多个使用拉普拉斯矩阵的一阶近似的局部图卷积层来达到相同的效果（用深度换广度）。

        由于在神经网络中，参数可以放大缩小，可以归一化，所以我们可以进一步假定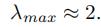

        因此，我们可以进一步将谱图卷积简化 （相当于上面切比雪夫多项式近似的时候，K取2，也就是只考虑1阶邻居）：

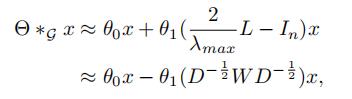
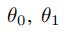        是谱图卷积核公用的参数。为了约束参数并为了稳定数值计算 ，θ0和θ1被一个参数θ代替：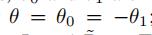

        

        我们再令

        

        

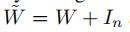
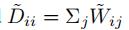
        那么我们有：

 

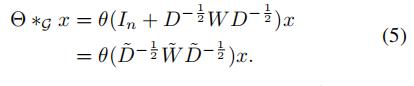
        堆叠K-1个一阶近似的图卷积可以获得和平行的K阶卷积相同的效果，所有的卷积可以从一个顶点的K-1阶邻居中获取到信息。

3.1.3 图卷积的泛化

         在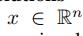上定义的谱图卷积算子*g可以延伸到多维度的标量中（每一个观测点的交通数据不再是一维而是多维）

        对于每个观测点有Ci个维度的交通信号数据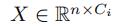，泛化的谱图卷积可以定义为：

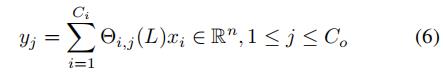
 其中，切比雪夫多项式的系数有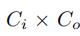个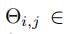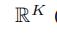，（Ci，Co分别表示输入和输出的大小）

        那么对于谱图卷积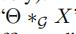来说，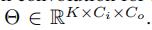 

 

        回到我们的问题，我们交通数据X的输入有M个时间片，交通路网途中一共有n个点，每个点有Ci维特征（在我们后续的数据中，Ci=1），即

3.2 提取空间特征的门控CNN、

         尽管基于RNN的模型被广泛应用于时间序列分析任务中，RNN在交通预测领域仍然面临着很多问题（迭代很费时间、复杂的门控机制、对于数据的动态变化相应较慢）

        相反地，CNN计算快，结构简单，可以并行，对于之前的步骤依赖性小。

        于是我们在时间轴上应用卷积操作来捕捉交通流数据的时间动态特征。

        如图所示，时间卷积网络包括了一个一维的因果卷积网络（卷积核大小为Kt）和一个门控线性单元GLU作为非线性激活函数。

        对于图G中的每一个点，时间卷积操作考虑它的Kt个邻居的信息。->每层时间卷积操作可以使得交通时间序列数据缩短Kt-1

        时间卷积层每一个点的输入可以看成是 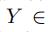 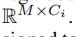（M——时间片长度，Ci每个点属性的维度值）

        时间卷积核，用来将输入Y映射到输出 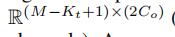上（P，Q是相同通道）

       

        因此，门控时间卷积可以写成

 

        这里 P和Q是GLU门的两个输入

        代表对应位置元素相乘的哈达玛积

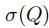        控制了哪些P是重要的，哪些P目前是不重要的

        

        相似地，时间卷积也可以泛化到三位变量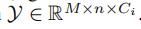

 3.3 时空卷积块

 

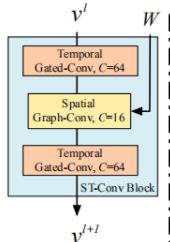
每一个时空卷积快最后都会过一个层归一化，来放置过拟合 

对于块l来说，它的输入为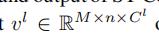

它的输出为 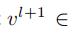 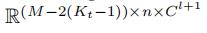（每一个时间卷积减少Kt-1维）

 整体ST卷积块的计算流程为：

 其中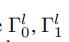是第一个和第二个时间卷积层的卷积核 

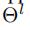 是空间谱图卷积层的卷积核

 

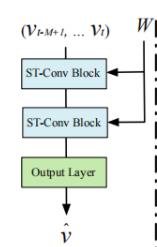
        在迭代了两个ST卷积块之后，我们使用了一个额外的时间卷积层，以及一个全连接层，来得到输出结果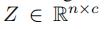 

         然后我们用一个线性变换获得每个点的预测速度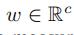，是权重向量，b是偏差

        我们使用L2 loss来衡量我们模型的优劣

 

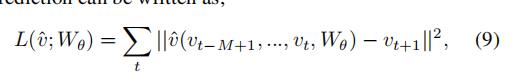
        这里Wθ是所有模型中可训练的参数

        v(t+1)是实际的交通速度 

3.4 STGCN总结

• STGCN可以用来处理结构化时间序列，不仅仅在交通领域，更多其它时空数据挖掘领域的数据都适用

• STGCN使用时间和空间上的卷积操作，这可以更好地捕捉时间和空间上的特征

• 由于模型是由完完全全的卷积结构组成，所以我们可以并行处理他，有更少的参数，更快的训练速度

4 实验部分

 

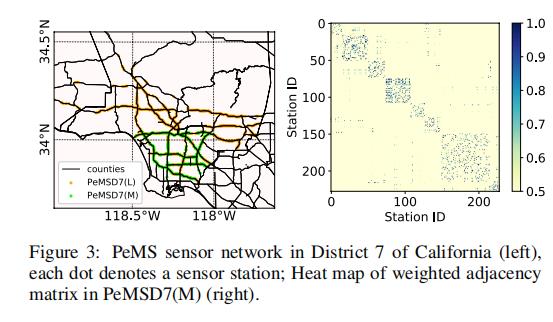
4.1 数据预处理 

        邻接矩阵由观测点之间的距离计算而得：        

 

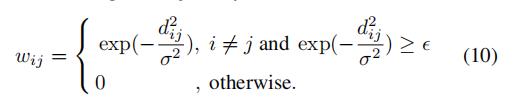
        ε和σ都是控制邻接矩阵稀疏程度的阈值

        邻接矩阵的可视化见上图（右）

4.2 实验结果

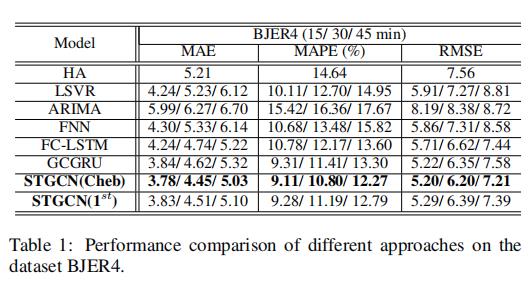
STGCN（Cheb）中的Kt设置为3 

         STGCN的预测表现是很不俗的

        传统的统计和机器学习方法可能在短期预测中效果不错，但是在中长期预测中，因为误差累积、缺少空间信息、没有记忆等问题，效果不理想

        ARIMA效果是最差的，因为它不能处理复杂的时空数据据

        深度学习方法比机器学习方法效果要好

 

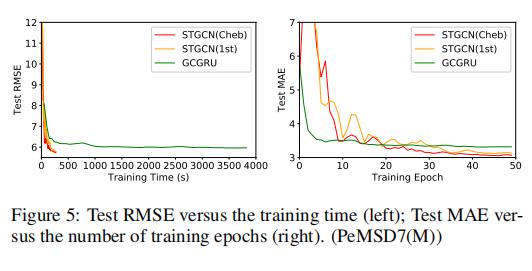
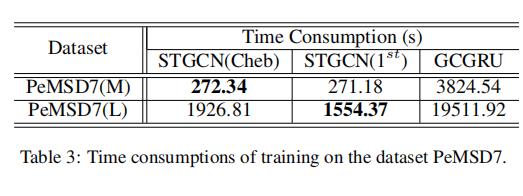
与此同时，模型的训练时间是很短的：