Pytorch之梯度下降和方向传播理论介绍

Posted 2021-09-06 WXiujie123456

目录

• • 梯度
  • 梯度下降
  • 梯度下降的一般求法：
  • • 批量梯度下降法BGD
    • 随机梯度下降法SGD
    • 小批量梯度下降法MBGD
  • 反向传播算法
  • 计算图和反向传播
  • 神经网络中的反向传播

梯度

梯度：是一个向量，学习(参数更新)的方向，导数+变化最快的方向。

梯度的本意是一个向量(矢量)，表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向(此梯度的方向)变化最快，变化率最大(为该梯度的模)。

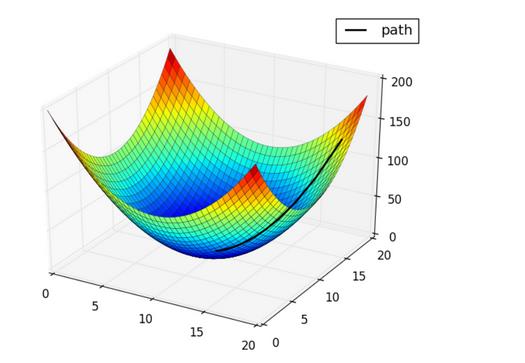
梯度下降

步骤(常用三种方法见后面小节)

算出梯度，梯度的计算公式：gradu=aₓ(∂u/∂x)+aᵧ(∂u/∂y)+az(∂u/∂z)

更新下一个取值点：wn=wn-1-α*gradun-1

梯度下降的一般求法：

批量梯度下降法BGD

批量梯度下降法(Batch Gradient Descent，简称BGD)是梯度下降法最原始的形式，它的具体思路是在更新每一参数时都使用所有的样本来进行更新，其数学形式如下：

(1) 对上述的能量函数求偏导：

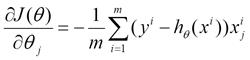
(2) 由于是最小化风险函数，所以按照每个参数的梯度负方向来更新每个：

具体的伪代码形式为：

repeat{　　　　

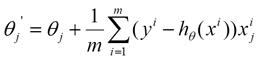
(for every j=0, … , n)

}

从上面公式可以注意到，它得到的是一个全局最优解，但是每迭代一步，都要用到训练集所有的数据，如果样本数目很大，那么可想而知这种方法的迭代速度！所以，这就引入了另外一种方法，随机梯度下降。

• **优点：**全局最优解；易于并行实现；
• **缺点：**当样本数目很多时，训练过程会很慢。

从迭代的次数上来看，BGD迭代的次数相对较少。其迭代的收敛曲线示意图可以表示如下：

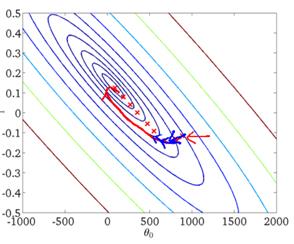
随机梯度下降法SGD

由于批量梯度下降法在更新每一个参数时，都需要所有的训练样本，所以训练过程会随着样本数量的加大而变得异常的缓慢。随机梯度下降法(Stochastic Gradient Descent，简称SGD)正是为了解决批量梯度下降法这一弊端而提出的。

将上面的能量函数写为如下形式：

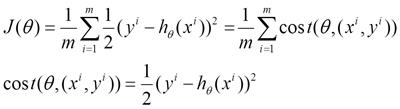
利用每个样本的损失函数对求偏导得到对应的梯度，来更新：

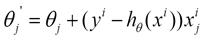
具体的伪代码形式为：

1. Randomly shuffle dataset；

2. repeat{

for i=1, … , {

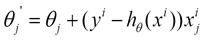
　　　　　(for j=0, … , )

}

}

随机梯度下降是通过每个样本来迭代更新一次，如果样本量很大的情况(例如几十万)，那么可能只用其中几万条或者几千条的样本，就已经将theta迭代到最优解了，对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。

• 优点：训练速度快；
• 缺点：准确度下降，并不是全局最优；不易于并行实现。

从迭代的次数上来看，SGD迭代的次数较多，在解空间的搜索过程看起来很盲目。其迭代的收敛曲线示意图可以表示如下：

小批量梯度下降法MBGD

有上述的两种梯度下降法可以看出，其各自均有优缺点，那么能不能在两种方法的性能之间取得一个折衷呢？即，算法的训练过程比较快，而且也要保证最终参数训练的准确率，而这正是小批量梯度下降法(Mini-batch Gradient Descent，简称MBGD)的初衷。

MBGD在每次更新参数时使用b个样本(b一般为10)，其具体的伪代码形式为：

Say b=10, m=1000.

Repeat{

for i=1, 11, 21, 31, … , 991{

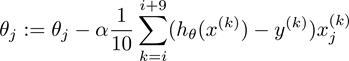
　　　　(for every j=0, … , )

}

}

反向传播算法

计算图和反向传播

计算图：通过图的方式来描述函数的图形

J(a,b,c)=3(a+bc)，令u=a+v,v=bc,把它绘制成计算图可以表示为：

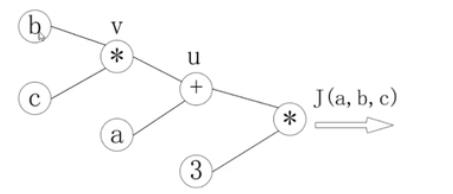
绘制成为计算图之后，可以清楚地看到向前计算的过程

之后，对每个节点求偏导可有：

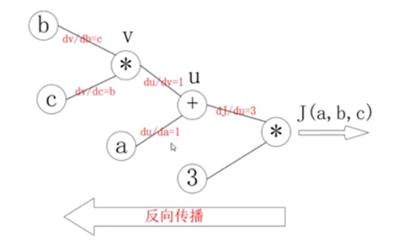
那么反向传播的过程就是一个上图从左往右的过程，自变量a,b,c各自的偏导就是连线上的梯度的乘积：

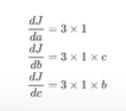
神经网络中的反向传播

个人总结：反向传播的作用还是想求某个值在某一点的偏导，从而确定梯度。反向传播借助由数据和操作构成的计算图，可以反向算出每一层的偏导，从而求出目标点的偏导。

神经网络的示意图

• w1,w2,…,wn表示网络第n层权重
• wn[I,j]表示第n层第i个神经元连接到第n+1层第j个神经元的权重

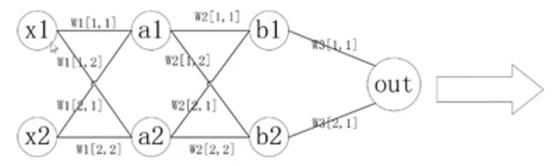
神经网络的计算图

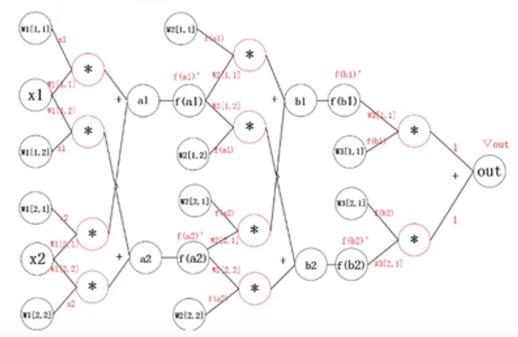
其中

f(x)是激活函数

▽out是根据损失函数对预测值进行求导得到的结果

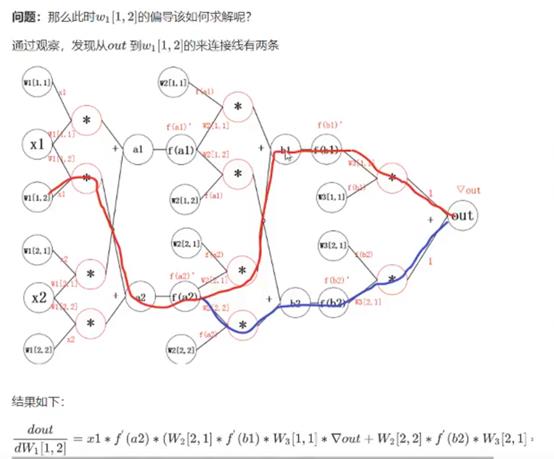
公式分为两部分：

• 括号外：左侧红线部分

• 括号内：

  ​ 加号左边：右边红线部分

  ​ 加号右边：右边蓝线部分

但是这样做有缺点：当模型很大时，计算量非常大

改进：用反向传播的思想，一层层的求出梯度，记录并更新(随之而来的缺点是需要额外空间存储临时数据)，如下所示：

计算过程如下：

更新参数之后，继续反向传播：

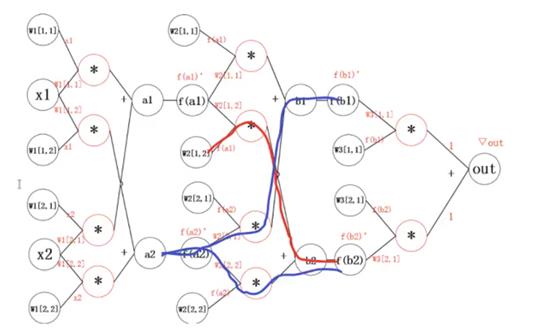
计算过程如下：

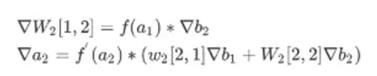
继续反向传播

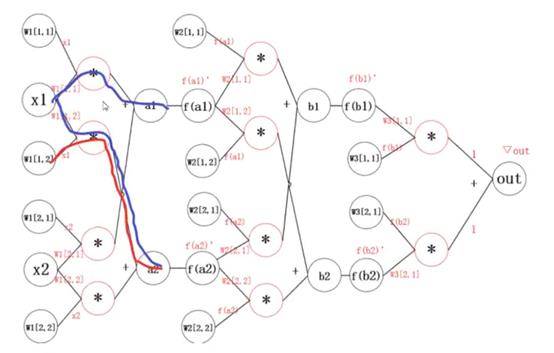
计算过程如下：

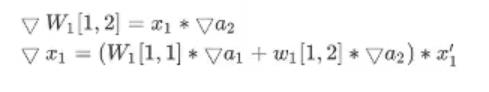
通用描述如下;

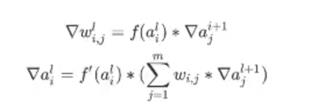
更多Pytorch知识梳理，请参考： pytorch学习笔记

有问题请下方评论，转载请注明出处，并附有原文链接，谢谢！如有侵权，请及时联系。