Pytorch实现线性回归

Posted 2021-09-06 WXiujie123456

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Pytorch实现线性回归相关的知识，希望对你有一定的参考价值。

向前计算

对于Pytorch中的一个tensor，如果设置它的属性.requires_grad为TRUE，那么它将会追踪对于该向量的所有操作。或者可以理解为，这个tensor是一个参数，后续会被计算梯度，更新该参数。

计算过程

假设有以下条件(1/4表示求均值，xi中有4个数)，使用torch完成其向前计算的过程。

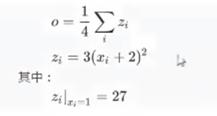
如果x为参数，需要对齐进行梯度的计算和更新

那么，在最开始随机设置x的值的过程中，需要设置的requires_grad属性为True，其默认值为False

import torch
x=torch.ones(2,2,requires_grad=**True**)
print(x)
y=x+2
print(y)
z=y*y*3
print(z)
out=z.mean()
print(out)

运行结果：

tensor([[1., 1.],

[1., 1.]], requires_grad=True)

tensor([[3., 3.],

[3., 3.]], grad_fn=)

tensor([[27., 27.],

[27., 27.]], grad_fn=)

tensor(27., grad_fn=)

从上述代码可以看出：

x的requires_grad属性为True

之后的每次计算都会修改其grad_fn属性，用来记录做过的操作，通过这个函数和grad_fn能够组成一个和前一小节类似的计算图

requires_grad和grad_fn

import torch
a=torch.randn(2,2)
print(a)
a=((a*3)/(a-1))
print(a)
print(a.requires_grad)
a.requires_grad=**True
# a.requires_grad(True)#**语法错误
print(a.requires_grad)
b=(a*a).sum()
print(b)
print(b.grad_fn)
with torch.no_grad():
   c=(a*a).sum()
 print(c.requires_grad)

运行结果：

tensor([[ 0.4826, 1.3892],

[-0.5649, 1.9469]])

tensor([[-2.7978, 10.7076],

[ 1.0829, 6.1681]])

False

True

tensor(161.6989, grad_fn=)

False

在此处，为了防止跟踪历史记录(和使用内存)，可以将代码块包装在with torch.no_grad()中，则它下面的代码块不会被追踪。这在评估模型时特别有用，因为模型可能具有requires_grad=True的可训练参数，但是我们不需要在此过程中对他们进行梯度计算。

梯度计算

对于“向前计算”那一节的out而言，我们可以使用backward方法来进行反向传播，计算梯度。out.backward()，此时就能求出out对x的倒数，调用x.grad能够获取导数值，得到：

tensor([[4.5000, 4.5000],

[4.5000, 4.5000]])

因为

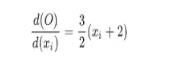
当xi=1时其值为4.5

附上面的完整代码：

x=torch.ones(2,2,requires_grad=True)
print(x)
y=x+2
print(y)
z=y*y*3
print(z)
out=z.mean()
print(out)
out.backward()#不可省略，使用了backward方法之后才可使用x.grad
print(x.grad)

注意：在输出为一个标量的情况下，我们调用输出tensor的backward()方法，但是在数据是一个向量的话，调用backward()还需要传入其他参数。

很多时候我们的损失函数是一个标量，所以此处不介绍损失为向量的情况

loss.backward()就是根据损失函数，对参数(require_grad=True)计算梯度，并且把它累加保存到x.grad，因为还并未更新其梯度，故每次反向传播之前需要把梯度置为0。

此外还需注意：

第一，关于tensor.data:

在tensor的require_grad=False时，tensor.data和tensor等价

require_grad=True时，tensor.data仅仅是获取tensor中的数据

第二，关于tensor.numpy()

require_grad=True不能直接转化，需要使用tensor.detach().numpy()

手动实现线性回归

假设我们的基础模型是y=wx+b,其中w和b均是参数，我们使用y=3x+0.8来构造数据x、y，所以最后通过模型应该能够得出w和b应该接近3和0.8

准备数据
计算预测值
计算损失，把参数的梯度置为0，进行反向传播
更新参数

话不多说，直接上代码：

#!/usr/bin/env python
# -*- coding:utf-8 -*-
import torch
import numpy as np
from matplotlib import pyplot as plt

#准备x，y的数值
x = torch.rand([50,1])#50行一列，x相当于采样点，在0-1间随机选50个点，越多越准确
y_true = 3*x + 0.8 #按照计算公式y的准确值

#通过模型计算y_predict
w = torch.rand(1,requires_grad=True)#随机产生一个w，并追踪梯度
b = torch.rand(1,requires_grad=True)##随机产生一个b，并追踪梯度
# y_predict = torch.matmul(x,w)+b#做乘法，相当于x*w+b

#计算损失，损失函数也可以替换成其他的损失函数
def loss_fn(y_true,y_predict):
    loss=(y_predict-y_true).pow(2).mean()#做差，平方，再取平均值
    for i in [w,b]:#每次梯度都要归零
        if i.grad is not None:
            i.grad.data.zero_()#加下划线就地修改
    loss.backward() #反向传播
    return loss.data

#优化w和b的值，使之接近真实数据3和0.8
def optimize(learning_rate):
    w.data = w.data - learning_rate * w.grad.data
    b.data -= learning_rate * b.grad.data

#通过循环，反向传播，更新参数
for i in range(3000):
   # #计算预测值
    y_predict = x * w + b
    #计算损失，把参数的梯度置为0，进行反向传播
    loss=loss_fn(y_true,y_predict)

    if i%500 == 0:
        print(i,loss.data,w.data,b.data)
    #更新参数w和b
    optimize(0.01)

#绘制图像，观测训练结束的预测值和真实值
predict=x*w + b
#plt绘制图像的数据需要是numpy类型的，不能是torch类型
plt.plot(x.numpy(),y_true.numpy(),c='r') #以点阵图的形式绘制
plt.scatter(x.numpy(),predict.detach().numpy())#以直线绘制，y_predeict是带有梯度的torch类型，所以需要使用.detach()方法或者.data属性获得不含梯度的张量数据
plt.show()

以上代码是用函数封装的，也可以写成线性的：

import numpy
import torch
from matplotlib import pyplot as plt

x = torch.rand([50])
y = 3*x + 0.8

w = torch.rand(1,requires_grad=True)
b = torch.rand(1,requires_grad=True)

learning_rate=0.01

for i in range(10000):
    y_predict = w * x + b
    loss = (y - y_predict).pow(2).mean()
    for j in [w,b]:
        if j.grad is not None:
            j.grad.data.zero_()
    loss.backward()
    w.data -= learning_rate * w.grad.data
    b.data -= learning_rate * b.grad.data

y_predict = w * x + b
plt.scatter(x.numpy(),y_predict.detach().numpy(),c='r')
plt.plot(x.numpy(),y.numpy())
plt.show()

Pytorch完成模型常用的API

在前一部分，我们手动实现了通过torch的相关方法完成反向传播和参数更新。但是在Pytorch中预设了一些更加灵活简单的对象，让我们的模型更加简单，让我们来构造模型、定义损失、优化损失等

nn.Mudule

nn.Mudule是torch.nn提供的一个类，是Pytorch中我们自定义网络中的一个基类，在这个类中定义了很多有用的方法。

在我们自定义网络时，有两个方法需要特别注意：

__init__()需要调用super方法，继承定义我们的网络的向量计算的过程
forward方法必须实现，用来定义我们的网络的向前计算的过程

用前面的y = wx + b的模型举例如下：

from torch import nn
class Lr(nn.Module):
    def __init__(self):
        super(Lr,self).__init__()
        self.linear = nn.Linear(1,1)

    def forward(self,x):
        out = self.linear(x)
        return out

注意：

1.nn.Linear为torch预定义好的线性模型，也被称为全链接层

class torch.nn.Linear(in_features，out_features，bias = True )

对传入数据应用线性变换：y = A x+ b

参数：

in_features - 每个输入样本的大小
out_features - 每个输出样本的大小
bias - 如果设置为False，则图层不会学习附加偏差。默认值：True

2.nn.Mudule定义了__call__方法，实现的就是调用forward方法，即Lr的实例，能够直接被传入参数调用，实际上调用的是forward方法并传入参数。

#实例化模型
model = Lr()
#传入参数，计算结果
predict = model(x)

优化器类optimizer

优化器(optimizer)，可以理解为torch为我们封装的用来进行更新参数的方法，比如常见的随机梯度下降(stochastic gradient descent，SGD)

优化器类都是由torch.optim提供的，例如：

torch.optim.SGD(参数，学习率)
torch.optim.Adam(参数，学习率)

注意：

参数可以使用model.parameters()来获取，获取模型中所有requires_grad = True的参数

优化类的使用方法：

实例化
将所有参数的梯度置为零
反向传播计算梯度
更新参数值

示例如下：

optimizer = optim.SGD(model.parameters(),lr=1e-3) #实例化优化器
optimizer.zero_grad()#梯度归零
loss.backward()#计算梯度
optimizer.step()#更新梯

损失函数

前面的例子是一个回归问题，torch中也预测了很多损失函数：

均方误差：nn.MSELoss()，常用于分类问题
交叉熵损失：nn.CrossEntropyLoss()，常用于逻辑回归

使用方法：

#实例化模型，loss和优化器
model = Lr()
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(),lr=1e-3)#实例化优化器
#训练模型
for i in range(30000):
   out = model(x) #获取预测值
   loss = criterion(y,out)#计算损失
   optimizer.zero_grad()#梯度归零
   loss.backward()#计算梯度
   optimizer.step()#更新梯度

线性回归完整代码

import torch
from torch import nn
from torch import optim
import numpy as np
from matplotlib import pyplot as plt

#定义数据
x = torch.rand([50,1])
y = x * 3 + 0.8

#定义模型
class Lr(nn.Module):
    def __init__(self):
        super(Lr,self).__init__()
        self.linear = nn.Linear(1,1)

    def forward(self,x):
        out = self.linear(x)
        return out

#实例化模型，loss和优化器
model = Lr()
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(),lr=1e-3)#实例化优化器
#训练模型
for i in range(30000):
    out = model(x) #获取预测值
    loss = criterion(y,out)#计算损失
    optimizer.zero_grad()#梯度归零
    loss.backward()#计算梯度
    optimizer.step()#更新梯度

#评估模型
model.eval()  #设置模型为评估模式，即预测模式
predict = model(x) #传入参数，计算结果
predict = predict.data.numpy()
plt.scatter(x.data.numpy(),y.data.numpy(),c='r')
plt.plot(x.data.numpy(),predict)
plt.show()

输出如下：

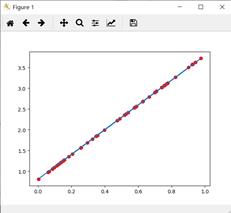
注意：

model.eval()表示设置模型为评估模式，即为估测模式
model.train(model=True)表示设置模式为训练模式

在当前的线性回归中，上述并无区别

但是在一些其他模型中，训练的参数和预测的参数会不相同，到时候就需要具体告诉程序我们选择哪种模式。

在GPU上运行代码

当模型太大，或者参数太多的情况下，为了加快训练速度，经常会使用GPU来进行训练

此时我们的代码需要稍作调整：

判断GPU是否可用 torch.cuda.is_available()

device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')

把模型参数和input数据转化为cuda的支持类型

x = torch.rand([50,1]).to(device)
model = Lr().to(device)

在GPU上计算结果也为cuda的数据类型，需要转化为numpy或者torch的cpu的tensor类型

predict = predict.cpu().detach().numpy()

detach()的效果和data的相似，但是detach()是深拷贝，data是取值，是浅拷贝。

修改后代码如下：

import torch
from torch import nn
# import torch.nn as nn
from torch import optim
import numpy as np
from matplotlib import pyplot as plt
#定义一个device对象
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
#定义数据
x = torch.rand([50,1]).to(device)
y = x * 3 + 0.8

#定义模型
class Lr(nn.Module):
    def __init__(self):
        super(Lr,self).__init__()
        self.linear = nn.Linear(1,1)

    def forward(self,x):
        out = self.linear(x)
        return out

#实例化模型，loss和优化器
model = Lr().to(device)
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(),lr=0.001)#实例化优化器
#训练模型
for i in range(30000):
    out = model(x) #获取预测值
    loss = criterion(y,out)#计算损失
    optimizer.zero_grad()#梯度归零
    loss.backward()#计算梯度
    optimizer.step()#更新梯度

#评估模型
model.eval()  #设置模型为评估模式，即预测模式
predict = model(x) #传入参数，计算结果
predict = predict.cpu().detach().numpy()
plt.scatter(x.data.numpy(),y.data.numpy(),c='r')
plt.plot(x.data.numpy(),predict)
plt.show()