机器学习系列文章——特征的处理与选择（归一化标准化降维PCA）

Posted 2021-09-06 棚鱼宴

一、特征处理

特征处理是通过特定的统计方法，将数据转化成算法要求的数据。其API为sklearn.preprocessing。先来看一组数据：

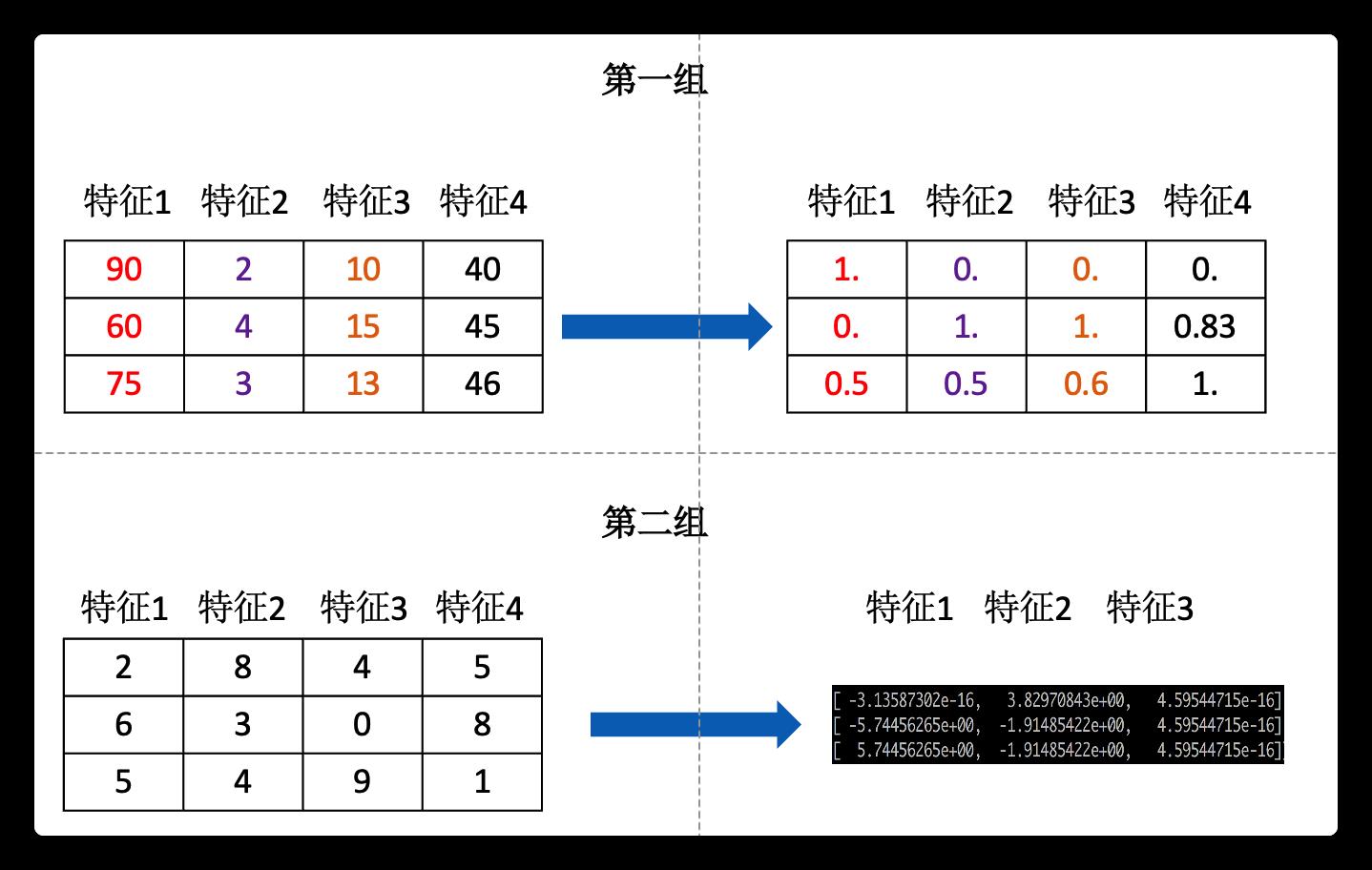
第一组中的特征1 相比于特征2而言大了几十倍，在正常处理时这些点即可视为异常点，影响统计结果分析。采用特征处理后转变为右侧的数据，可以更加方便的处理而不会产生异常值。
常见的处理方法如下：

数据类型	处理方法
数值型数据	归一化、标准化、缺失值
类别型数据	one hot编码
时间型数据	时间的切分

（ 一）归一化

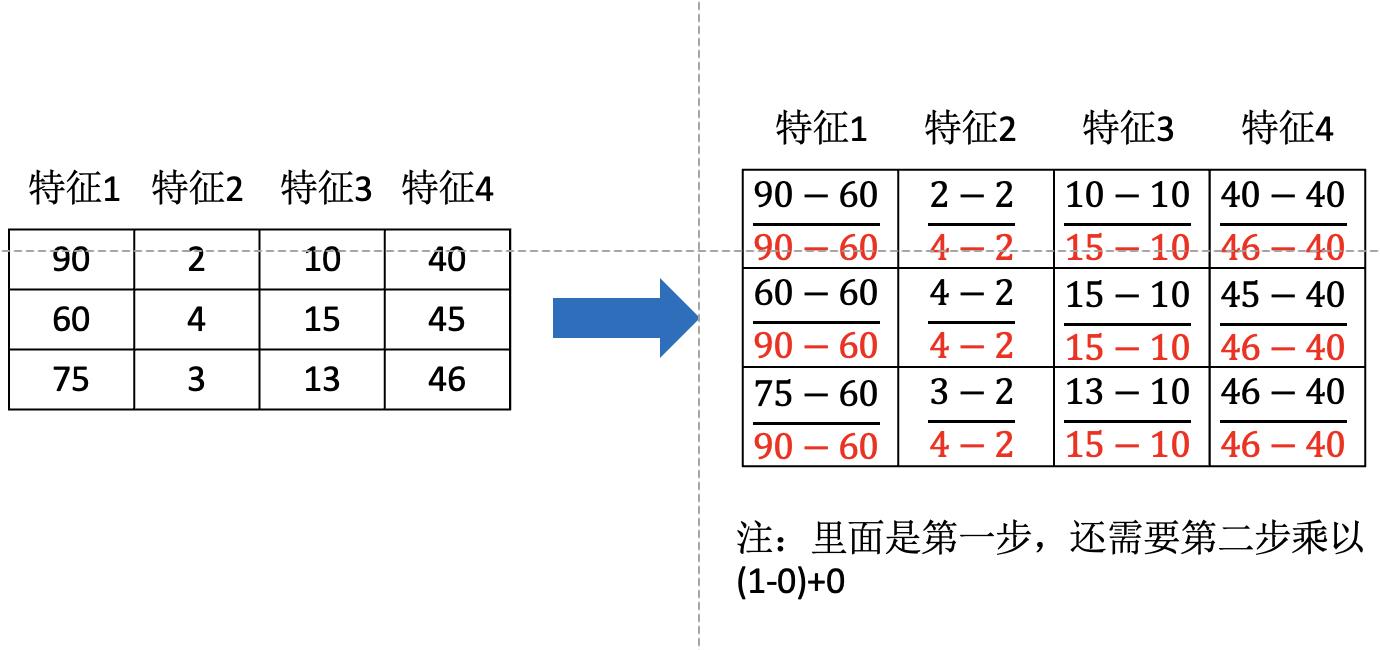
归一化是通过对原始数据进行变换把数据映射到一定范围（默认0-1）之间。其公式为：

归一化实例：

# 导入特征处理api及其子库
from sklearn.preprocessing import MinMaxScaler,StandardScaler,Imputer
# 定义一个归一化处理函数
def mm(data):
    """归一化处理"""
    # 实例化mm
    mm=MinMaxScaler(feature_range=(2,3))
    # 调用fit_transform来处理数据
    data=mm.fit_transform(data)
    print("归一化处理后的数据为：")
    print(data)
    return None

data=[[90, 2, 10, 40], [60, 4, 15, 45], [75, 3, 13, 46]]
mm(data=data)

归一化处理后，原本的数据全部集中在（2-3）之间。

注意在特定场景下最大值最小值是变化的，另外，最大值与最小值非常容易受异常点影响，所以这种方法鲁棒性较差，只适合传统精确小数据场景。

（二）标准化

对于归一化来说：如果出现异常点，影响了最大值和最小值，那么结果显然会发生改变

对于标准化来说：如果出现异常点，由于具有一定数据量，少量的异常点对于平均值的影响并不大，从而方差改变较小。

def std(data):
    """标准化处理数据"""
    # 实例化
    sd=StandardScaler()
    data=sd.fit_transform(data)
    print("标准化处理后的数据为：")
    print(data)
    return None
data=[[90, 2, 10, 40], [60, 4, 15, 45], [75, 3, 13, 46]]
std(data=data)

标准化方法，在已有样本足够多的情况下比较稳定，适合现代嘈杂大数据场景。

（三）缺失值处理方法

缺失值的处理一般分为两种，其一为删除，其一为填补。当缺失数据达到一定比例时，采取删除法，当数据量较小，可填补每行或每列的平均值或中位数。其api为Imputer

def im(data):
    """缺失值处理"""
    # 实例化,将平均值填充至缺失值
    im=Imputer(missing_values='NaN', strategy='mean', axis=0)
    data=im.fit_transform(data)
    print("缺失值处理后的数据为：")
    print(data)
    return None
data=[[90, 2, 10, np.nan], [60, np.nan, 15, 45], [75, 3, 13, 46]]
im(data=data)

二、特征选择

在实际的数据中，数据量大、特征冗杂且很多特征之间存在较大的相关性。部分噪声对预测结果有负影响。

如上图，在机器学习识别鸟的种类时，如上四个特征哪几个是需要的？可以看出，第三个特征和第四个有较大的相关性，较为冗余。因此在处理之前有必要对数据的特征进行一次选择。
特征选择就是单纯地从提取到的所有特征中选择部分特征作为训练集特征，特征在选择前和选择后可以改变值、也不改变值，但是选择后的特征维数肯定比选择前小，毕竟我们只选择了其中的一部分特征，同时也降低了识别学习的难度。

（一）Filter(过滤式):VarianceThreshold

低方差意味着数据较为集中，差异不大。因此选择过滤式方法过滤掉方差较小的特征是一个不错的办法。

from sklearn.feature_selection import VarianceThreshold
def var(data):
    """
    特征选择-删除低方差的特征
    :return: None
    """
    # 将方差小于1的数据舍弃
    var = VarianceThreshold(threshold=1.0)

    data = var.fit_transform(data)
    print("方差处理后的数据为：")

    print(data)
    return None
data=[[0, 2, 0, 3], [0, 1, 4, 3], [0, 1, 1, 3]]
var(data=data)

（二）降维处理 主成分分析法（PCA)

PCA的本质是一种简化分析的技术，其目的是将数据维数压缩，尽可能降低原数据的维度，损失少量信息。

        简化前                             简化后

from sklearn.decomposition import PCA
def pca(data):
    """主成分分析"""
    # n_components=0.9-损失的数据信息为10%
    pca=PCA(n_components=0.9)
    data=pca.fit_transform(data)
    print("降维后的数据为：")
    print(data)
    return None
data=[[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]]
pca(data=data)

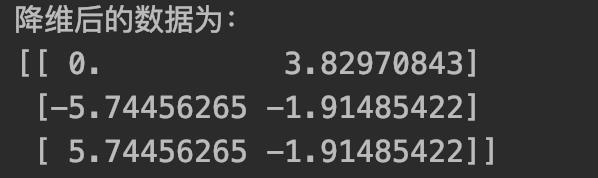
保留了原始数据90%的信息的同时，将原数据从三维降低至二维。

以上为机器学习中特征的处理与选择相关的方法，后续将介绍机器学习常用的模拟器。