0x51.动态规划 - 线性DP(习题详解 × 10)
Posted 繁凡さん
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了0x51.动态规划 - 线性DP(习题详解 × 10)相关的知识,希望对你有一定的参考价值。
目录
本系列博客是《算法竞赛进阶指南》的学习笔记,包含书中的部分重要知识点、例题解题报告及我个人的学习心得和对该算法的补充拓展,仅用于学习交流和复习,无任何商业用途。博客中部分内容来源于书本和网络 ,由我个人整理总结。部分内容由我个人编写而成,如果想要有更好的学习体验或者希望学习到更全面的知识,请于京东搜索购买正版图书:《算法竞赛进阶指南》——作者李煜东,强烈安利,好书不火系列,谢谢配合。
%
学习笔记目录链接: 学习笔记目录链接
%
整理的算法模板合集: ACM模板
%
点我看算法全家桶系列!!!
0x51.动态规划 - 线性DP
线性DP指具有线性 “阶段” 划分的动态规划算法被统称为线性DP。
无论线性DP的状态表示是一维的还是多维的,都是 “的线性上的递推 ”。DP的阶段沿着各个维度线性增长,从一个或多个边界点开始有方向地向整个状态空间转移、拓展。最后每个状态上都保留了以自身为 “目标” 的子问题的最优解。
0x51.1 LIS问题
问题描述 :最长上升子序列,给定一个长度为 n 的数列 A,求数值单调递增的子序列的长度最长是多少。
状态表示: f [ i ] f[i] f[i] 表示以 A [ i ] A[i] A[i] 为结尾的 “最长上升子序列” 的长度
阶段划分:子序列的结尾位置(数列 A 中的位置,从前到后)
转移方程: f [ i ] = max { f [ j ] + 1 ∣ 0 ≤ j < i , A [ j ] < A [ i ] } f[i]=\\max\\{f[j] + 1 \\mid 0\\le j<i, A[j]<A[i]\\} f[i]=max{f[j]+1∣0≤j<i,A[j]<A[i]}
边界: f [ 0 ] = 0 f[0] = 0 f[0]=0
目标: max { f [ i ] ∣ 1 ≤ i ≤ n } \\max\\{f[i]\\mid 1\\le i\\le n\\} max{f[i]∣1≤i≤n}
时间复杂度 :暴力 O ( n 2 ) O(n^2) O(n2), 二分优化 / 数据结构优化 O ( n log n ) O(n\\log n) O(nlogn)
空间复杂度: O ( n ) O(n) O(n)
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 7;
int n, m;
int a[N];
int f[N];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; ++ i)
scanf("%d", &a[i]);
f[0] = 1;
for (int i = 1; i <= n; ++ i) {
f[i] = 1;
for (int j = 1; j < i; ++ j) {
if(a[j] < a[i])
f[i] = max(f[i], f[j] + 1);
}
}
int ans = 0;
for (int i = 1; i <= n; ++ i)
ans = max(ans, f[i]);
cout << ans << endl;
return 0;
}
二分优化
//二分优化,直接维护这个上升序列,把上升序列存到栈里,遇到小的就贪心地把栈里更大的换掉,遇到大的就放到栈里
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 6, INF = 0x3f3f3f3f;
int n, m;
int a[N];
int f[N], cnt;
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; ++ i)
scanf("%d", &a[i]);
int ans = 0;
f[0] = -INF;
for (int i = 1; i <= n; ++ i) {
if(a[i] > f[cnt]) f[ ++ cnt] = a[i];
else *lower_bound(f + 1, f + 1 + cnt, a[i]) = a[i];
}
cout << cnt << endl;
}
Problem A. 登山 (最长下降子序列)
AcWing 1014
五一到了,ACM队组织大家去登山观光,队员们发现山上一共有 N N N 个景点,并且决定按照顺序来浏览这些景点,即每次所浏览景点的编号都要大于前一个浏览景点的编号。
同时队员们还有另一个登山习惯,就是不连续浏览海拔相同的两个景点,并且一旦开始下山,就不再向上走了。
队员们希望在满足上面条件的同时,尽可能多的浏览景点,你能帮他们找出最多可能浏览的景点数么?
2 ≤ N ≤ 1000 2≤N≤1000 2≤N≤1000
Solution
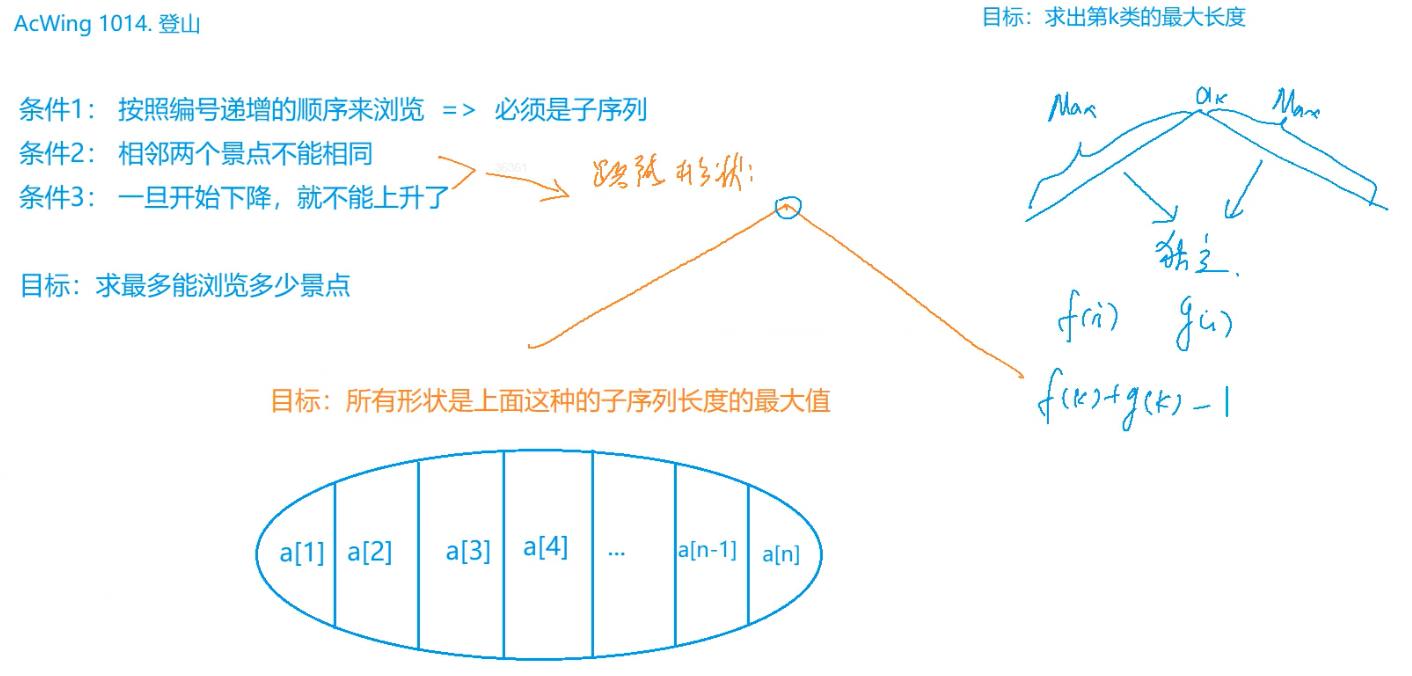
本题实际上是求一个最大上升子序列到一个点,然后再以该点为起点求一个最长下降子序列。所以我们可以先预处理出正向的最长上升子序列,再求一个逆向的最长上升子序列(就是最长下降子序列),然后枚举每一个点作为起点,求一个最大值。要注意的是枚举的这个起点被两个子序列算了两次,所以要 -1。
Code
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1010, M = 50007, INF = 0x3f3f3f3f;
int n, m;
int t;
int a[N], f[N], g[N];
int main(){
scanf("%d",&n);
for(int i = 1;i <= n;++i)
scanf("%d",&a[i]);
for(int i = 1;i <= n;++ i){
f[i] = 1;
for(int j = 1;j < i;++j)
if(a[j] < a[i])
f[i] = max(f[i], f[j] + 1);
}
for(int i = n;i >= 1;-- i){
g[i] = 1;
for(int j = n;j > i;--j)
if(a[j] < a[i])
g[i] = max(g[i],g[j] + 1);
}
int res = 0;
for(int i = 1;i <= n;++i)
res = max(res, f[i] + g[i] - 1);
printf("%d\\n",res);
return 0;
}
Problem B. 友好城市(思维)
AcWing 1012
Palmia国有一条横贯东西的大河,河有笔直的南北两岸,岸上各有位置各不相同的 N N N 个城市。
北岸的每个城市有且仅有一个友好城市在南岸,而且不同城市的友好城市不相同。
每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市,但是由于河上雾太大,政府决定避免任意两条航道交叉,以避免事故。
编程帮助政府做出一些批准和拒绝申请的决定,使得在保证任意两条航线不相交的情况下,被批准的申请尽量多。
1 ≤ N ≤ 5000 , 0 ≤ x i ≤ 10000 1≤N≤5000,0≤x_i≤10000 1≤N≤5000,0≤xi≤10000
Solution
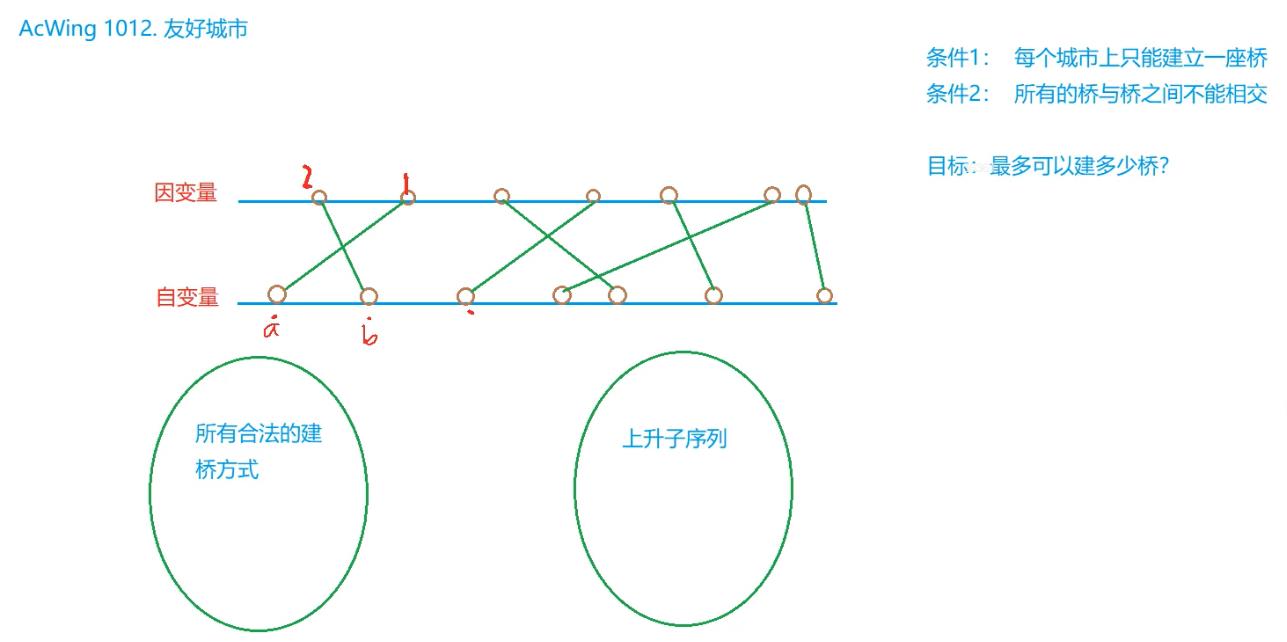
当 i > j i>j i>j且 i 友 > j 友 i_{友}>j_友 i友>j友时不交叉
所以可以将南岸从小到大排序 求北岸的最长上升子序列
Code
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 5000007, M = 5000007, INF = 0x3f3f3f3f;
typedef pair<int,int> PII;
int n, m;
int b[N];
int f[N];
PII a[N];
int len = 1;
int main(){
scanf("%d",&n);
for(int i = 1;i <= n;++i){
scanf("%d%d",&a[i].first, &a[i].second);
}
sort(a + 1,a + 1 + n);
f[1] = a[1].second;
for(int i = 2;i <= n;++i){
if(f[len] < a[i].second)f[++len] = a[i].second;
else {
//int tmp = lower_bound(f + 1, f + 1 + len, a[i].second) - f;
//f[tmp] = a[i].second;
*lower_bound(f + 1 ,f + 1 + len,a[i].second) = a[i].second;
}
}
printf("%d\\n",len);
return 0;
}
Problem C. 最大上升子序列和
AcWing 1016
一个数的序列 b i b_i bi,当 b 1 < b 2 < … < b S b_1<b_2<…<b_S b1<b2<…<bS 的时候,我们称这个序列是上升的。
对于给定的一个序列 ( a 1 , a 2 , … , a N ) (a_1,a_2,…,a_N) (a1,a2,…,aN) ,我们可以得到一些上升的子序列 ( a i 1 , a i 2 , … , a i K ) (a_{i_1},a_{i_2},…,a_{i_K}) (ai1,ai2,…,aiK) ,这里 1 ≤ i 1 < i 2 < … < i K ≤ N 1≤i_1<i_2<…<i_K≤N 1以上是关于0x51.动态规划 - 线性DP(习题详解 × 10)的主要内容,如果未能解决你的问题,请参考以下文章