LeetCode233. 数字1的个数(数位dp)/1583. 统计不开心的朋友(模拟)/112. 路径总和 / 230. 二叉搜索树中第K小的元素 /968. 监控二叉树(树形dp)
Posted Zephyr丶J
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了LeetCode233. 数字1的个数(数位dp)/1583. 统计不开心的朋友(模拟)/112. 路径总和 / 230. 二叉搜索树中第K小的元素 /968. 监控二叉树(树形dp)相关的知识,希望对你有一定的参考价值。
233. 数字 1 的个数
2021.8.13 每日一题
题目描述
给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。
示例 1:
输入:n = 13
输出:6
示例 2:
输入:n = 0
输出:0
提示:
0 <= n <= 2 * 10^9
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/number-of-digit-one
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
之前阿里一道笔试题和这个很像
之前剑指offer做过,知道是按每一位来取,但是还是忘了怎么做了
具体就是看每一位的范围,例如4563中十位上出现1的个数,首先明确出现1的范围就是0010-4519,那么不看1的话,范围就是000-459,也就是460个数,所以这个数中十位出现1的个数就是460
因为当前位位0和1 比较特殊,所以特别考虑一下
class Solution {
public int countDigitOne(int n) {
//剑指offer的题,我记得是一个个数位进行计算的
//对于个位来说,1,11,21,..,91,101,111,121,..,991,1001每十个数有一个1
//对于十位来说,10-19,110-119,210-219..1010-1019
//百位100-199,200-299,1100-1199
int res = 0;
int digit = 1; //当前位,刚开始是个位,1
int high = n / 10; //高位
int low = 0; //低位
int cur = n % 10; //当前位
while(high != 0 || cur != 0){
//对于当前位是0,比如100,那么个位1的个数就是high*digit,十位就是1* 10
if(cur == 0)
res += high * digit;
//如果当前位是1,比如4213,十位1的个数位:0010-4213,去掉十位,000-423,high * dight + low + 1
else if(cur == 1)
res += high * digit + low + 1;
else{
//如果当前位是其他数,例如4353,十位1的个数:范围0010-4319,去掉十位就是000-439,也就是440个
res += (high + 1) * digit;
}
low += cur * digit;
cur = high % 10;
high = high / 10;
digit *= 10;
}
return res;
}
}
数位DP学习一下:
学习weiwei哥的题解
https://leetcode-cn.com/problems/number-of-digit-one/solution/shu-wei-dpjava-by-liweiwei1419-awxv/
注释应该写的很清楚了,关键思想是把数分成块部分和剩余部分,然后逐位求解;挺不好想的。
class Solution {
public int countDigitOne(int n) {
//数位dp,主要是学思想
String s = String.valueOf(n);
char[] cc = s.toCharArray();
int l = cc.length;
if(l == 1)
return n == 0 ? 0 : 1;
//整块中的1的个数,比如9,99,999
int[] block = new int[l - 1];
//9只有1个
block[0] = 1;
//递推,后面99就有9 * block[0] + 10; 999就有百位固定是1--100 + 10 * block[i - 1]
for(int i = 1; i < l - 1; i++){
block[i] = 10 * block[i - 1] + (int)Math.pow(10, i);
}
//余项中1的个数,这个dp[i]表示右边向左数第i + 1位
int[] dp = new int[l];
dp[0] = cc[l - 1] == '0' ? 0 : 1;
for(int i = 1; i < l; i++){
char c = cc[l - i - 1];
//如果当前为是0,那么0xxx中包含0的个数就和xxx中包含0的个数相同
if(c == '0')
dp[i] = dp[i - 1];
//如果当前为1,那么1xxx中包含1的个数,就等于整块0-999中包含1的个数,
//再加上1000-1xxx中千位为1的个数,也就是xxx+1
//再加上1000-1xxx中除去千位,也就是000-xxx中1的个数,也就是dp[i - 1]
else if(c == '1'){
//首先1000-1xxxx,取出xxx的值
String sub = s.substring(l - i, l);
int part1 = Integer.valueOf(sub) + 1;
dp[i] = dp[i - 1] + block[i - 1] + part1;
//如果大于1,和第二种情况其实差不多,就是例如5xxx
//块就是0-999,1000-1999,--4000,4999,有5个整块
//而5000-5xxx的个数,相当于000-xxx的个数,也就是dp[i - 1]
//容易忽略的一点,就是上面1000-1999中其实只计算了000-999的1的个数,千位为1的个数还没有被计算
}else{
dp[i] = dp[i - 1] + (c - '0') * block[i - 1] + (int)Math.pow(10, i);
}
}
return dp[l - 1];
}
}
1583. 统计不开心的朋友
2021.8.14 每日一题
题目描述
给你一份 n 位朋友的亲近程度列表,其中 n 总是 偶数 。
对每位朋友 i,preferences[i] 包含一份 按亲近程度从高到低排列 的朋友列表。换句话说,排在列表前面的朋友与 i 的亲近程度比排在列表后面的朋友更高。每个列表中的朋友均以 0 到 n-1 之间的整数表示。
所有的朋友被分成几对,配对情况以列表 pairs 给出,其中 pairs[i] = [xi, yi] 表示 xi 与 yi 配对,且 yi 与 xi 配对。
但是,这样的配对情况可能会是其中部分朋友感到不开心。在 x 与 y 配对且 u 与 v 配对的情况下,如果同时满足下述两个条件,x 就会不开心:
x 与 u 的亲近程度胜过 x 与 y,且
u 与 x 的亲近程度胜过 u 与 v
返回 不开心的朋友的数目 。
示例 1:
输入:n = 4, preferences = [[1, 2, 3], [3, 2, 0], [3, 1, 0], [1, 2, 0]], pairs = [[0, 1], [2, 3]]
输出:2
解释:
朋友 1 不开心,因为:
- 1 与 0 配对,但 1 与 3 的亲近程度比 1 与 0 高,且
- 3 与 1 的亲近程度比 3 与 2 高。
朋友 3 不开心,因为:- 3 与 2 配对,但 3 与 1 的亲近程度比 3 与 2 高,且
- 1 与 3 的亲近程度比 1 与 0 高。
朋友 0 和 2 都是开心的。
示例 2:
输入:n = 2, preferences = [[1], [0]], pairs = [[1, 0]]
输出:0
解释:朋友 0 和 1 都开心。
示例 3:
输入:n = 4, preferences = [[1, 3, 2], [2, 3, 0], [1, 3, 0], [0, 2, 1]], pairs = [[1, 3], [0, 2]]
输出:4
提示:
2 <= n <= 500
n 是偶数
preferences.length == n
preferences[i].length == n - 1
0 <= preferences[i][j] <= n - 1
preferences[i] 不包含 i
preferences[i] 中的所有值都是独一无二的
pairs.length == n/2
pairs[i].length == 2
xi != yi
0 <= xi, yi <= n - 1
每位朋友都 恰好 被包含在一对中
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/count-unhappy-friends
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
模拟这个过程就可以了
代码注释写的很详细了:
class Solution {
public int unhappyFriends(int n, int[][] preferences, int[][] pairs) {
//看到这个题,一瞬间不知道该怎么做
//暴力找吗
//首先4个人是一组
//想想模拟的过程,首先,对于第一个人x,找到与第一个人配对的人y,
//然后遍历,找到x与其中一个人的亲近程度大于y的,例如有a,b,c
//然后再找到这个人配对的人,查看这个人配对的人是亲密程度是否大于x
//首先,为了方便查找配对的人,将pairs关系写在哈希表中
Map<Integer, Integer> map = new HashMap<>();
for(int i = 0; i < n / 2; i++){
map.put(pairs[i][0], pairs[i][1]);
map.put(pairs[i][1], pairs[i][0]);
}
int res = 0;
for(int i = 0; i < n; i++){
//与x配对的人
int y = map.get(i);
//找与x亲密度大于y的
for(int j = 0; j < n - 1; j++){
if(preferences[i][j] == y)
break;
//与u的亲密度大于y
int u = preferences[i][j];
//与u配对的v
int v = map.get(u);
boolean flag = false;
for(int k = 0; k < n - 1; k++){
//如果先遇到x,就标记为true
if(preferences[u][k] == i){
flag = true;
break;
}
//否则false
if(preferences[u][k] == v){
break;
}
}
if(flag){
res++;
break;
}
}
}
return res;
}
}
我这里三层循环,超了百分之五十多,还可以通过哈希表优化到两层
通过存储两个人关系的分数,或者下标,能够在O1的复杂度内查找出哪些人与x的亲密度大于y,具体不写了,感觉意义不大,速度还不一定比我这个快
112. 路径总和
题目描述
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ,判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。
叶子节点 是指没有子节点的节点。
示例 1:
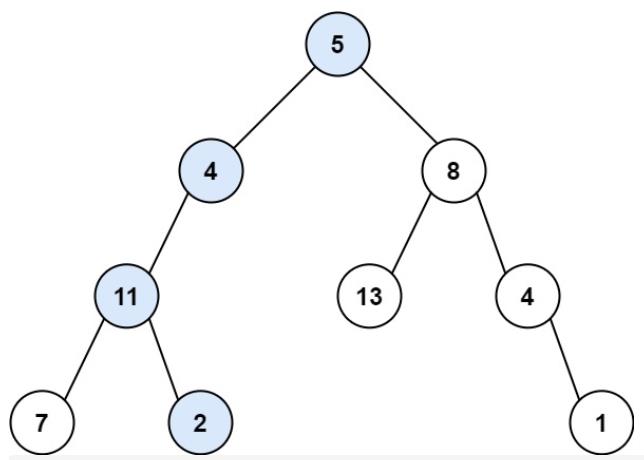
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
示例 2:
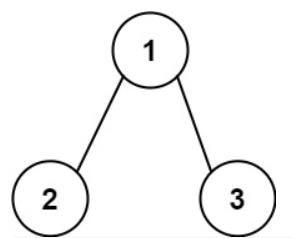
输入:root = [1,2,3], targetSum = 5>
输出:false
示例 3:
输入:root = [1,2], targetSum = 0
输出:false
提示:
树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/path-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
错了两次,还写出来这么垃圾的代码…
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if(root == null)
return false;
return dfs(root, targetSum);
}
public boolean dfs(TreeNode root, int target){
if(root.val == target && root.left == null && root.right == null)
return true;
if(root == null)
return false;
boolean l = false;;
if(root.left != null)
l = dfs(root.left, target - root.val);
if(l)
return true;
boolean r = false;
if(root.right != null)
r = dfs(root.right, target - root.val);
return r;
}
}
看官解这个,优雅
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean hasPathSum(TreeNode root, int sum) {
if (root == null) {
return false;
}
if (root.left == null && root.right == null) {
return sum == root.val;
}
return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
}
}
230. 二叉搜索树中第K小的元素
题目描述
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。
示例 1:
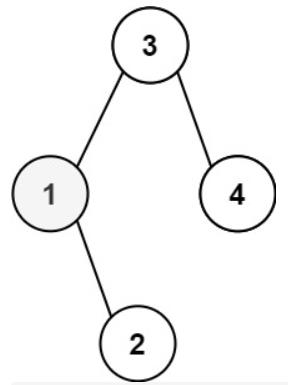
输入:root = [3,1,4,null,2], k = 1
输出:1
示例 2:
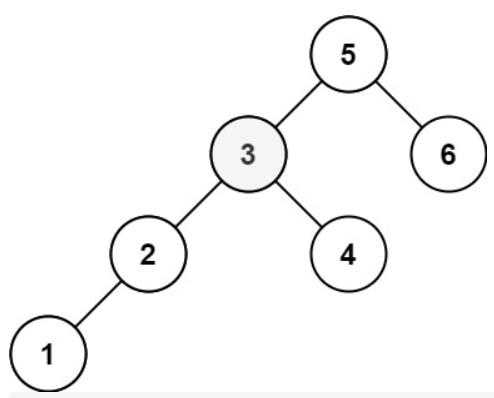
输入:root = [5,3,6,2,4,null,null,1], k = 3
输出:3
提示:
树中的节点数为 n 。
1 <= k <= n <= 10^4
0 <= Node.val <= 10^4
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/kth-smallest-element-in-a-bst
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
int k;
TreeNode t = null;
public int kthSmallest(TreeNode root, int k) {
//第k小就是从小到大数第k个
//就是中序遍历的第k个节点
this.k = k;
inorder(root);
return t.val;
}
public void inorder(TreeNode node){
if(node == null)
return;
if(t != null)
return;
inorder(node.left);
if(--k == 0)
t = node;
inorder(node.right);
}
}
968. 监控二叉树
题目描述
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
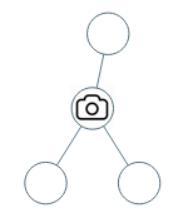
输入:[0,0,null,0,0]
输出:1
解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
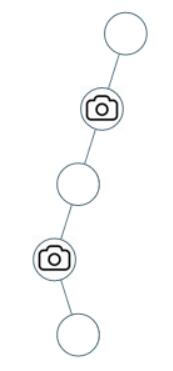
输入:[0,0,null,0,null,0,null,null,0]
输出:2
解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/binary-tree-cameras
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
一个简单的思路,基于贪心
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
int res = 0;
public int minCameraCover(TreeNode root) {
//carl哥的递归思路
//首先是贪心的想法,叶子结点尽量被父节点的摄像头所覆盖
//所以需要从底向上推导,就想到了后序遍历
//3种状态,0没有被覆盖,1有摄像头,2被覆盖
//对于空节点,需要是被覆盖的状态,才会使叶子结点是无覆盖的状态
//然后分情况讨论即可
//如果根节点是未被覆盖的状态,那么需要安装摄像头
if(postorder(root) == 0)
res++;
return res;
}
public int postorder(TreeNode node){
//如果当前节点为空,状态为被覆盖
if(node == null)
return 2;
int l = postorder(node.left);
int r = postorder(node.right);
//如果左右都被覆盖了,那么此时根节点应该不被覆盖
if(l == 2 && r == 2){
return 0;
}
//如果左右有一个没有被覆盖,那么此时根节点必须要有一个摄像头
if(l == 0 || r == 0){
res++;
return 1;
}
//如果左右节点有摄像头,那么当前节点是被覆盖的情况
if(l == 1 || r == 1){
return 2;
}
return -1;
}
}
主流做法, 树形dp
/*
树形dp的通用解法
状态定义:
状态0:当前节点安装相机的时候,需要的最少相机数
状态1: 当前节点不安装相机,但是能被覆盖到的时候,需要的最少相机数
状态2:当前节点不安装相机,也不能被覆盖到的时候,需要的最少相机数
最后我们的解当然就是根节点的状态0和状态1中的最小值啦
而每一个节点的状态只和它的左孩子和右孩子有关,因此状态的转移方式如下:
安装相机,其左孩子节点和右孩子节点都可以安装或者不装,但是总相机数+1
dp[0] = Math.min(left[0], Math.min(left[1], left[2])) + Math.min(right[0], Math.min(right[1], right[2])) + 1
不安装相机,但是能被覆盖到,说明其孩子节点至少有一个安装了相机,因为自己不安装相机,如果孩子节点也不安装,那个节点只能是已被覆盖到的
dp[1] = Math.min(left[0] + Math.min(right[0], right[1]), right[0] + Math.min(left[0], left[1]))
不安装相机,也不能被覆盖到,说明其孩子节点都没有安装相机,因为自己没有安装相机,其孩子节点也必须是已被覆盖到的
dp[2] = left[1] + right[1]
*/
class Solution {
public int minCameraCover(TreeNode root) {
int[] res = check(root);
return Math.min(res[0], res[1]);
}
public int[] check(TreeNode root){
int[] dp = new int[3];
//如果遍历到空,那么赋初值
if(root == null){
//因为如果为空,那么这个点不可能装摄像头
dp[0] = Integer.MAX_VALUE / 2;
//同时这个点是未覆盖的情况,这个可有可无
//dp[2] = Integer.MAX_VALUE / 2;
return dp;
}
int[] left = check(root.left);
int[] right = check(root.right);
//如果当前节点有摄像头,左右可以有摄像头也可以没有,也可以没有被覆盖
dp[0] = Math.min(left[0], Math.min(left[1], left[2])) + Math.min(right[0], Math.min(right[1], right[2])) + 1;
//如果当前节点没有摄像头,但是被覆盖了,那么左右孩子肯定有一个有摄像头
dp[1] = Math.min(left[0] + Math.min(right[0], right[1]), right[0] + Math.min(left[0], left[1]));
//如果当前节点没有摄像头,也没有被覆盖,那么左右孩子肯定是被覆盖但没有摄像头
dp[2] = left[1