AtCoder Beginner Contest 214（补题）

Posted 2021-09-06 佐鼬Jun

C - Distribution

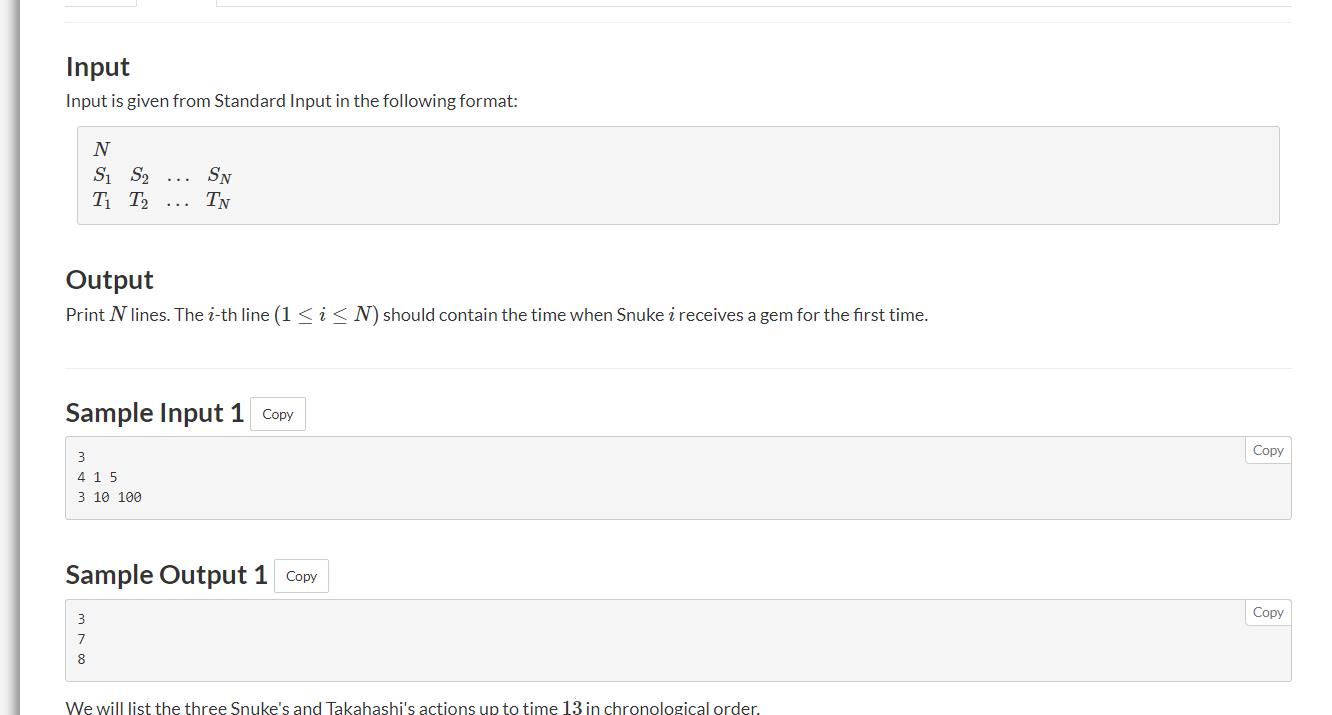
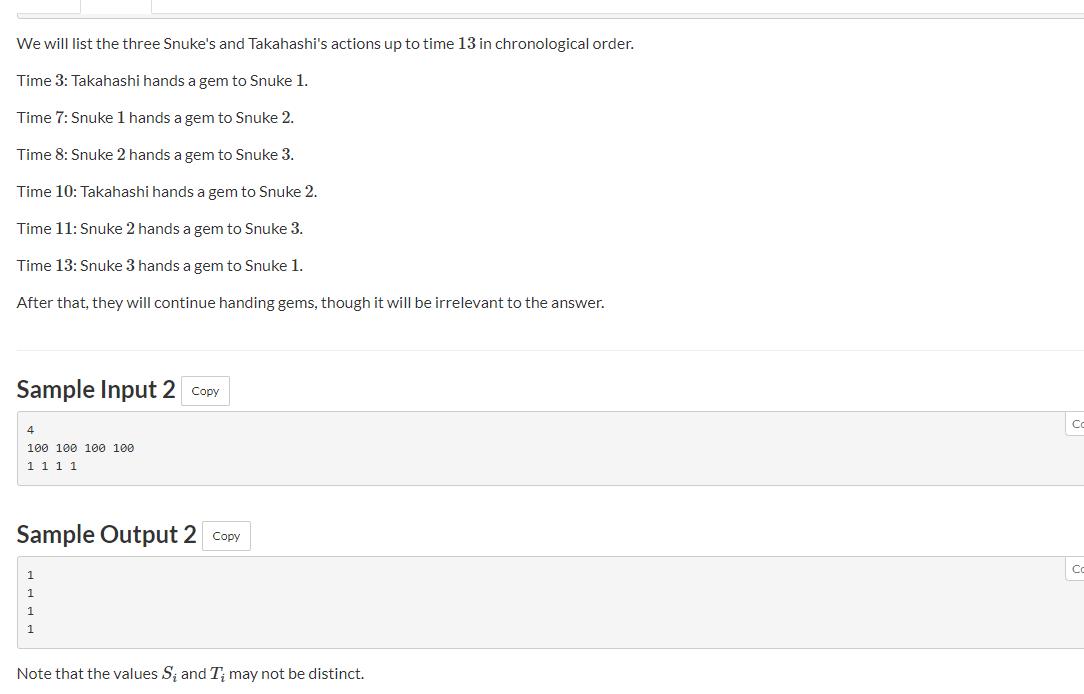
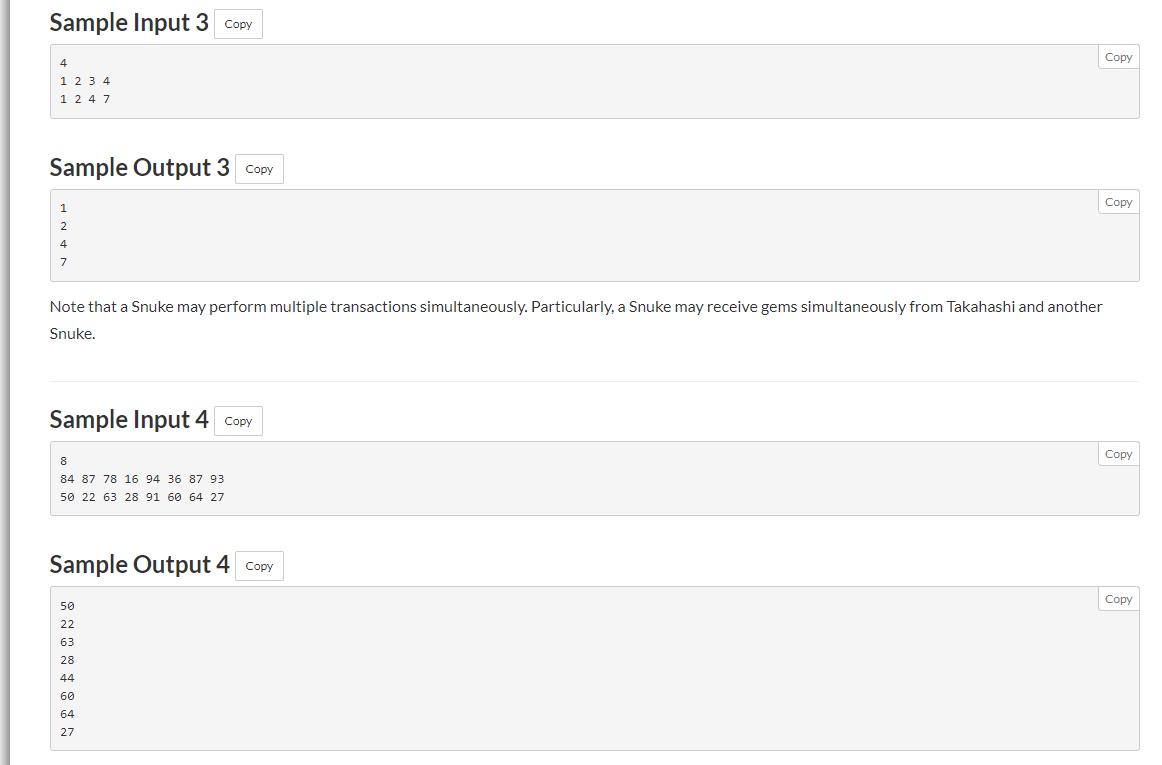
题意： 每个人都会在$t$这个时间得到一个宝石,每个人都会处理宝石$s$时间，所以第$i$个人会在$t_i$时间得到宝石，并在$ti+si$时间给第$i+1$个人，第$n$个人会给第$1$个人，现在问每个人第一次得到宝石的时间是什么时候。
思路： 先找第一个得到宝石的人，从这个人开始往后循环找，从第1个得到宝石的人开始，后面的所有人的第一颗宝石要么使 是前一个人给他的，要么使在$t_i$这个时间得到的，直接在两者之间取最小值。

#include <bits/stdc++.h>
using namespace std;
const int N = 3e5 + 10;
#define ll long long
struct node {
    ll s, t;
    ll x;
} a[N];
int main() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%lld", &a[i].s);
    }
    for (int i = 0; i < n; i++) {
        scanf("%lld", &a[i].t);
    }
    int j = -1;
    for (int i = 0; i < n; i++) {
        if (a[i].t < a[j].t || j == -1) {
            j = i;
        }
    }
    int now = 0;
    ll res = 0;
    a[j].x = a[j].t;
    res = a[j].t;
    for (int i = (j + 1) % n; now < n; i = (i + 1) % n, now++) {
        if (i == 0) {
            a[i].x = min((ll)a[i].t, (ll)a[n - 1].s + res);
        } else
            a[i].x = min((ll)a[i].t, (ll)a[i - 1].s + res);
        res = a[i].x;
    }
    for (int i = 0; i < n; i++) {
        printf("%lld\\n", a[i].x);
    }
    return 0;
}

D - Sum of Maximum Weights

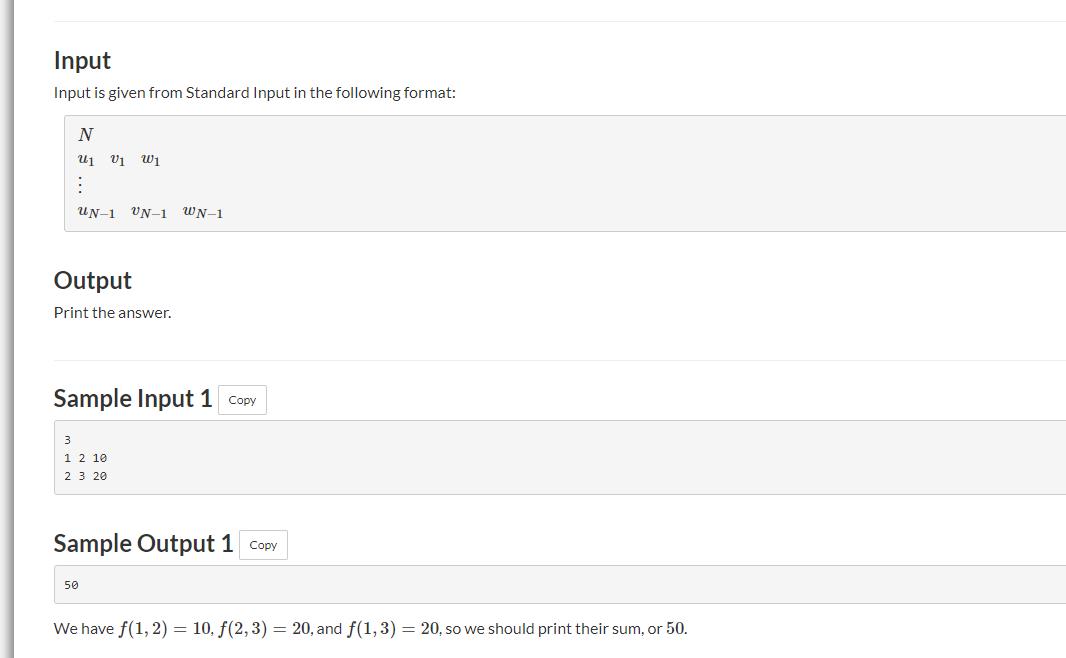
题意： 给一颗有权树，$n$个点，$n-1$条边，每个边的边权$w_i$,定义$f(u,v)$为u和v路径上最大边权所对应的边的权值，现在让你求
$\sum _{i=1}^{N-1}\sum _{j=i+1}^{N}f(u,v)$
思路： 题意其实就是求每个点对之间的$f(u,v)$并求和。原来的求和公式时间复杂度太高一定不可行，求的是任意点对之间的值，所以只要想办法在限定时间内能弄出所有情况就行。点对之间不好枚举，发现可以枚举边权，对于每个边权(如果它是当前连接两个连通块的边中最大的一个)，它所产生的贡献就是$w_i\cdot 左边连通块大小\cdot 右边连通块大小$，要保证这个边是连接两个连通块的边中最大的一个，可以排序(根据边权，从小到大)，每次枚举边权的时候，边求当前这条边所产生的贡献，边建立连通块。因为所有边都枚举过了，所以所有点对都会被枚举出来
核心思想：并查集每次更新当前这个边权所连接的两个连通块

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
#define ll long long
struct node {
    int u, v, w;
    bool operator<(node p) const { return w < p.w; }
} edge[N];
int fa[N];
ll S[N];
ll res;
int n;
int find(int x) {
    if (x != fa[x]) fa[x] = find(fa[x]);
    return fa[x];
}

ll Union(int a, int b) {
    int x = find(a), y = find(b);
    ll res = (ll)S[x] * S[y];
    fa[x] = y;
    S[y] += S[x];
    return res;
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        fa[i] = i, S[i] = 1;
    }
    for (int i = 1; i <= n - 1; i++) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        edge[i] = {a, b, c};
    }
    sort(edge + 1, edge + n);
    for (int i = 1; i < n; i++) {
        res += (ll)edge[i].w * Union(edge[i].u, edge[i].v);
    }
    cout << res << endl;
}

E - Packing Under Range Regulations

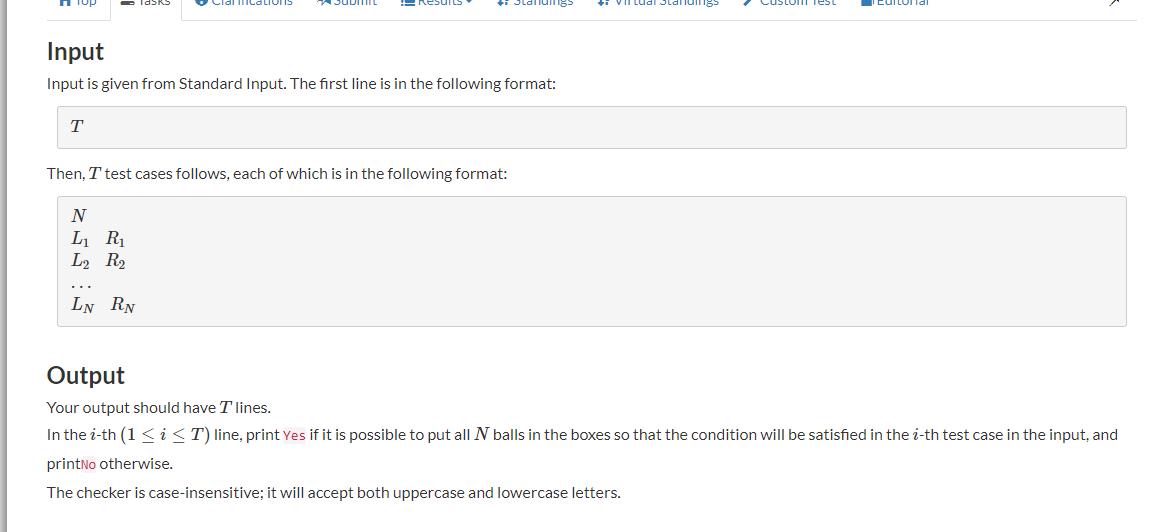
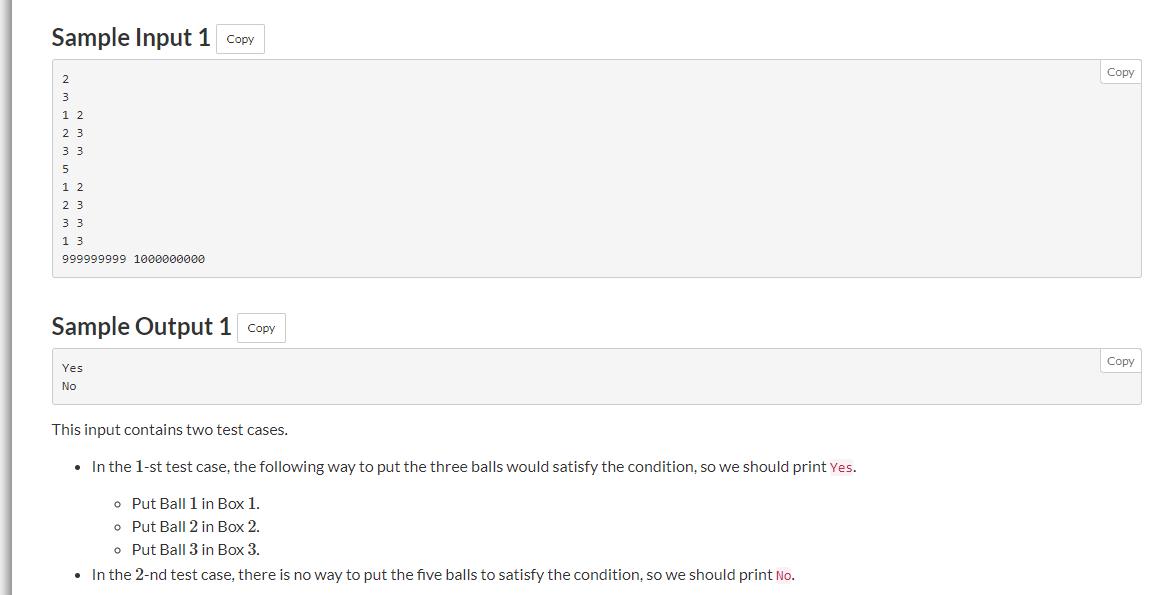
题意： 有$10^9$个盒子，每个盒子只能放一个求，现在有$n$个球，编号为从1到$n$,现在每个球都有一个放的位置区间$[L,R]$,现在给你所有求放置的可能区间，问所有球能否满足给定的条件，放进盒子里。
思路： 贪心的思想，对于给定的球的放置区间$[L_i,R_i]$,在满足一个盒子放一个球的条件下，尽量往左球，因为可能有好几个球的左区间是一样的，但右区间不一样，这样尽量往左放，可以给后面和他左区间一样，但右区间比它小的腾出空间，而且往左放，也对那些左区间与当前右区间有重叠的做了贡献，相当于越往左放，对于后面的贡献越大。所以按照右区间大小从小到大排序，然后每次取出一个区间，尽可能地往左放，当要放的位置，超过了区间的右界限，那就是不合法的。

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
struct node {
    int l, r;
} a[N];
map<int, int> fa;
int n;
int find(int x) {
    if (fa.count(x)) {
        return fa[x] = find(fa[x]);
    }
    return x;
}
bool cmp(node a, node b) { return a.r < b.r; }

int main() {
    int t;
    scanf("%d", &t);
    while (t--) {
        fa.clear();
        bool flag = 1;
        cin >> n;
        for (int i = 1; i <= n; i++) {
            scanf("%d%d", &a[i].l, &a[i].r);
        }
        sort(a + 1, a + n + 1, cmp);
        for (int i = 1; i <= n; i++) {
            //当前区间地最左端(能放的情况下)
            int x = find(a[i].l);
            fa[x] = x + 1;
            if (x > a[i].r) {
                flag = 0;
                puts("No");
                break;
            }
        }
        if (flag) puts("Yes");
    }
    return 0;
}

To be continued
如果你有任何建议或者批评和补充，请留言指出，不胜感激