机器学习基石VC dimension
Posted 桃陉
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习基石VC dimension相关的知识,希望对你有一定的参考价值。
写在前面
本节我们主要引入了 V C d i m e n s i o n VC \\ dimension VC dimension 的概念,从简单的感知机模型的 V C VC VC 维度推到一般的感知机模型 V C VC VC 维度,最后加深了对其理解。
本文整理自台湾大学林轩田的《机器学习基石》
1. VC dimension 的定义
∙ \\bullet ∙ 首先我们对上一次的内容进行一下回顾。
上一次我们证明了
B
(
N
,
k
)
B(N,k)
B(N,k) 存在上限的上限为
N
k
−
1
N^{k-1}
Nk−1。根据下面具体的表格内容显示,我们发现当
N
≥
2
,
k
≥
3
N≥2,k≥3
N≥2,k≥3 时,完全可以写成(简化了等式):
m
H
(
N
)
≤
N
k
−
1
m_{H}(N)≤N^{k-1}
mH(N)≤Nk−1
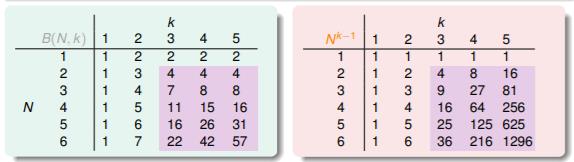
那么上一次提到的公式也可以进行转换,对于任意的
g
=
A
(
D
)
∈
H
g=A(D)∈H
g=A(D)∈H 并且数据样本
D
D
D 足够大且
k
≥
3
k≥3
k≥3 时,有:
P
D
(
∣
E
i
n
(
g
)
−
E
o
u
t
(
g
)
∣
>
ϵ
)
≤
4
m
H
(
2
N
)
e
−
1
8
ϵ
2
N
≤
4
(
2
N
)
k
−
1
e
−
1
8
ϵ
2
N
P_{D}(\\left | E_{in}(g)-E_{out}(g) \\right | >\\epsilon) ≤4m_{H}(2N)e^{-\\frac{1}{8}\\epsilon^{2}N}≤4(2N)^{k-1}e^{-\\frac{1}{8}\\epsilon^{2}N}
PD(∣Ein(g)−Eout(g)∣>ϵ)≤4mH(2N)e−81ϵ2N≤4(2N)k−1e−81ϵ2N
此时, m H ( N ) m_{H}(N) mH(N) 存在 b r e a k p o i n t break \\ point break point,说明拥有好的 h y p o t h e s i s ( H ) {\\color{Violet}hypothesis(H)} hypothesis(H); N N N 取足够大,说明拥有好的 d a t a ( D ) {\\color{Violet}data(D)} data(D);演算法 A A A 中选择的 g g g 具有小的 E i n E_{in} Ein,说明拥有好的 A {\\color{Violet}A} A;在具备了这些条件以后机器就可以进行学习了!
∙
\\bullet
∙
V
C
d
i
m
e
n
s
i
o
n
{\\color{Brown}VC \\ dimension}
VC dimension:它指的是不超过
b
r
e
a
k
p
o
i
n
t
break \\ point
break point 的最大的数(maximum)。记为
d
v
c
d_{vc}
dvc 用公式表示就为:
d
v
c
=
′
m
i
n
i
m
u
m
k
′
−
1
d_{vc}='minimum \\ k'-1
dvc=′minimum k′−1
当
N
≤
d
v
c
N≤d_{vc}
N≤dvc 时,N个点都可以被区分开来。
当
N
>
d
v
c
N>d_{vc}
N>dvc 时,N个点不可以可以被区分开来。最多区分
k
−
1
k-1
k−1 个点。
所以当
N
≥
2
N≥2
N≥2,
d
v
c
≥
2
d_{vc}≥2
dvc≥2 时,
m
H
(
N
)
≤
N
d
v
c
m_{H}(N)≤N^{d_{vc}}
mH(N)≤Ndvc。
对于我们前面提到的几种成长函数来说,它们都有各自的 V C d i m e n s i o n VC \\ dimension VC dimension:
▹
\\triangleright
▹
p
o
s
i
t
i
v
e
r
a
y
s
:
d
v
c
=
1
positive \\ rays : d_{vc}=1
positive rays:dvc=1
▹
\\triangleright
▹
p
o
s
i
t
i
v
e
i
n
t
e
r
v
a
l
s
:
d
v
c
=
2
positive \\ intervals : d_{vc}=2
positive intervals:dvc=2
▹
\\triangleright
▹
c
o
n
v
e
x
s
e
t
s
:
d
v
c
=
∞
convex \\ sets : d_{vc}=\\infty
convex sets:dvc=∞
▹
\\triangleright
▹
2
D
p
e
r
c
e
p
t
r
o
n
s
:
d
v
c
=
3
2D \\ perceptrons : d_{vc}=3
2D perceptrons:dvc=3
∙ \\bullet ∙ 练习
这里有一组 N N N 个点的输入,它们不能被 H H H 完全区分,那么下面关于 d v c ( H ) d_{vc}(H) dvc(H) 的哪个说法时正确的?
a.
d
v
c
(
H
)
>
N
d_{vc}(H)>N
dvc< 以上是关于机器学习基石VC dimension的主要内容,如果未能解决你的问题,请参考以下文章