MTT 模板(任意模数)
Posted 爷灬傲奈我何123
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了MTT 模板(任意模数)相关的知识,希望对你有一定的参考价值。
MTT能处理任意模数的FFT。就比如这题
题意: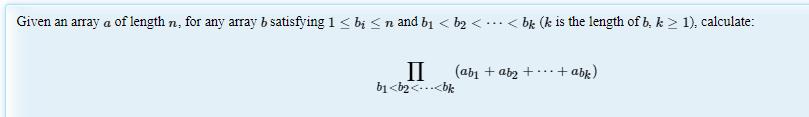
求一个数列长度大于等于1的子序列和的乘积,首先考虑N^2 DP
DP[i][j]代表考虑前i个数和为j的方案数,很容易处理出方案数,最后答案就是
Π
s
u
m
D
P
[
s
u
m
]
\\Pi sum^{DP[sum]}
ΠsumDP[sum]。
还有另一种解法,考虑生成函数,对于每一个数选或者不选,把TA变成多项式的情形,就是
1
+
x
a
i
1+x^{ai}
1+xai然后乘起来,最后每个某个数M的答案就是
x
m
x^m
xm的系数,考虑幂次太大,我们要欧拉降幂一下,mod=998244353,%(mod-1),由于mod-1没有好的性质,我们可以任意模数NTT或者FFT拆系数,这里用FFT拆系数来实现,由于要乘N次多项式,时间复杂度
O
(
n
2
l
o
g
n
)
O(n^2logn)
O(n2logn)并且多项式的乘积是可交换的,我们考虑分治一下,每次用
(
l
,
m
i
d
)
∗
(
m
i
d
+
1
,
r
)
(l,mid)*(mid+1,r)
(l,mid)∗(mid+1,r)能优化到
n
l
o
g
n
l
o
g
n
nlognlogn
nlognlogn
ps:MTT部分是看的杨大佬的模板,拿来吧你
struct MTT {
long double PI=acos(-1);
int rev[N];
int bit,limit;
struct Complex {
long double x,y;
void init() { x=y=0; }
Complex operator + (const Complex& t) const { return {x+t.x,y+t.y}; }
Complex operator - (const Complex& t) const { return {x-t.x,y-t.y}; }
Complex operator * (const Complex& t) const { return {x*t.x-y*t.y,x*t.y+y*t.x}; }
}p1[N],p2[N],g[N];
void init(int n,int m) {
int x=n+m; bit=0;
while((1<<bit)<=x) bit++;
limit=1<<bit;
for(int i=0;i<limit;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
}
void fft(Complex a[],int inv) {
for(int i=0;i<limit;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int mid=1;mid<limit;mid<<=1) {
Complex w1=Complex({cos(PI/mid),inv*sin(PI/mid)});
for(int i=0;i<limit;i+=mid*2) {
Complex wk=Complex({1,0});
for(int j=0;j<mid;j++,wk=wk*w1) {
Complex x=a[i+j],y=wk*a[i+j+mid];
a[i+j]=x+y; a[i+j+mid]=x-y;
}
}
}
}
int mul(int *as,int *a,int n,int *b,int m,int mod) {
for(int i=0;i<n;i++) {
int x=a[i];
int aa=x>>15,bb=x&0x7fff;
p1[i]={(long double)aa,(long double)bb};
p2[i]={(long double)aa,-(long double)bb};
}
for(int i=0;i<m;i++) {
int x=b[i];
int aa=x>>15,bb=x&0x7fff;
g[i]={(long double)aa,(long double)bb};
}
init(n,m);
fft(p1,1); fft(p2,1); fft(g,1);
for(int i=0;i<limit;i++) g[i].x/=limit,g[i].y/=limit;
for(int i=0;i<limit;i++) p1[i]=p1[i]*g[i],p2[i]=p2[i]*g[i];
fft(p1,-1); fft(p2,-1);
for(int i=0;i<=m+n;i++) {
ll ans=0,a1b1=0,a2b2=0,a1b2=0,a2b1=0;
a1b1=(long long)floor((p1[i].x+p2[i].x)/2+0.49)%mod;
a1b2=(long long)floor((p1[i].y+p2[i].y)/2+0.49)%mod;
a2b1=((long long)floor(p1[i].y+0.49)-a1b2)%mod;
a2b2=((long long)floor(p2[i].x+0.49)-a1b1)%mod;
ans=(((((a1b1<<15)%mod+(a1b2+a2b1))%mod)<<15)%mod+a2b2)%mod;
ans+=mod; ans%=mod;
as[i]=ans;
}
for(int i=0;i<limit;i++) p1[i].init(),p2[i].init(),g[i].init();
return n+m;
}
}MT;
int all,al[N*4];
};
S T D : STD: STD:
//#pragma GCC target("avx")
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast")
// created by myq
#include<iostream>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<climits>
#include<cmath>
#include<cctype>
#include<stack>
#include<queue>
#include<list>
#include<vector>
#include<set>
#include<map>
#include<sstream>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long ll;
#define x first
#define y second
typedef pair<int,int> pii;
const int N = 400010;
const int mod=998244353;
inline int read()
{
int res=0;
int f=1;
char c=getchar();
while(c>'9' ||c<'0')
{
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9')
{
res=(res<<3)+(res<<1)+c-'0';
c=getchar();
}
return res;
}
const double eps=1e-6;
int n,m;
int a[N];
struct MTT {
long double PI=acos(-1);
int rev[N];
int bit,limit;
struct Complex {
long double x,y;
void init() { x=y=0; }
Complex operator + (const Complex& t) const { return {x+t.x,y+t.y}; }
Complex operator - (const Complex& t) const { return {x-t.x,y-t.y}; }
Complex operator * (const Complex& t) const { return {x*t.x-y*t.y,x*t.y+y*t.x}; }
}p1[N],p2[N],g[N];
void init(int n,int m) {
int x=n+m; bit=0;
while((1<<bit)<=x) bit++;
limit=1<<bit;
for(int i=0;i<limit;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
}
void fft(Complex a[],int inv) {
for(int i=0;i<limit;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int mid=1;mid<limit;mid<<=1) {
Complex w1=Complex({cos(PI/mid),inv*sin(PI/mid)});
for(int i=0;i<limit;i+=mid*2) {
Complex wk=Complex({1,0});
for(int j=0;j<mid;j++,wk=wk*w1) {
Complex x=a[i+j],y=wk*a[i+j+mid];
a[i+j]=x+y; a[i+j+mid]=x-y;
}
}
}
}
int mul(int *as,int *a,int n,int *b,int m,int mod) {
for(int i=0;i<n;i++) {
int x=a[i];
int aa=x>>15,bb=x&0x7fff;
p1[i]={(long double)aa,(long double)bb};
p2[i]={(long double)aa,-(long double)bb};
}
for(int i=0;i<m;i++) {
int x=b[i];
int aa=x>>15,bb=x&0x7fff;
g[i]={(long double)aa,(long double)bb};
}
init(n,m);
fft(p1,1); fft(p2,1); fft(g,1);
for(int i=0;i<limit;i++) g[i].x/=limit,g[i].y/=limit;
for(int i=0;i<limit;i++) p1[i]=p1[i]*g[i],p2[i]=p2[i]*g[i];
fft(p1,-1); fft(p2,-1);
for(int i=0;i<=m+n;i++) {
ll ans=0,a1b1=0,a2b2=0,a1b2=0,a2b1=0;
a1b1=(long long)floor((p1[i].x+p2[i].x)/2+0.49)%mod;
a1b2=(long long)floor((p1[i].y+p2[i].y)/2+0.49