基础莫队|暴力|扫描线＋树状数组CF220 B: Little Elephant and Array

Posted 2021-09-06 biu~跃哥冲冲冲

Problem Little Elephant and Array

评测传送门

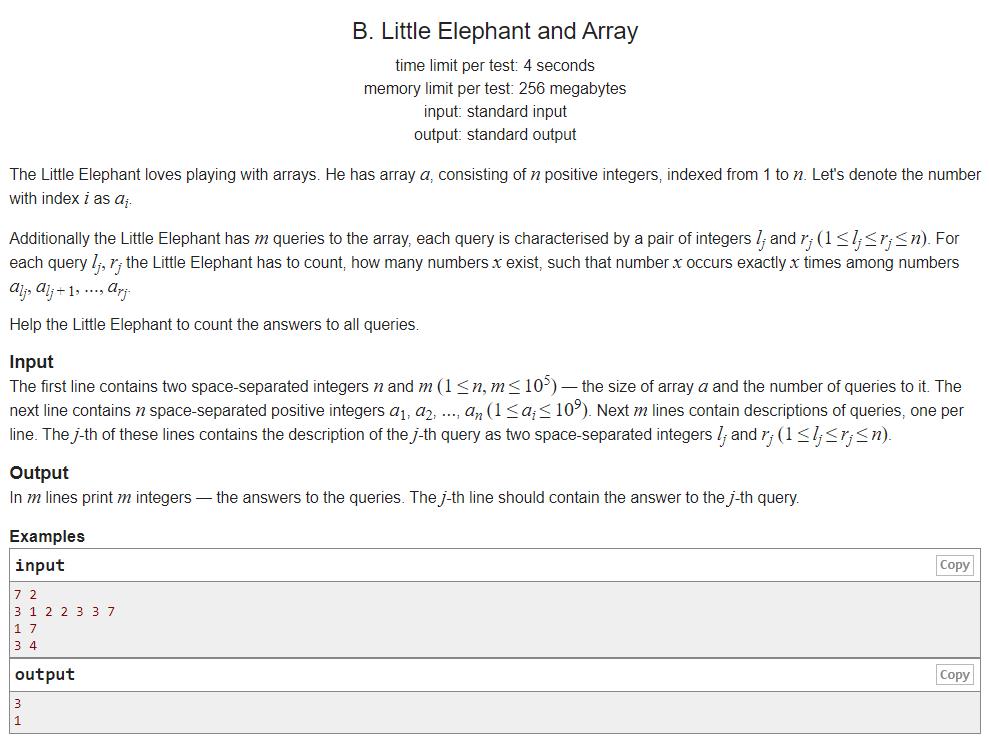
题目大意：
给出长度为 $n$ 的一个序列，有 $m$ 组询问，每组询问给出一个区间，左端点 $l$ ,右端点 $r$, 查询区间$[l,r]$中有多少个数 $x$ 的出现次数恰好也等于 $x$, 符号语言表达就是$cnt[x]=x$.

解题思路：
对于这个题的解法有好多种，在这里我简单的分析一二。
一：莫队解法
对于莫队算法，最经典的题目应该是HH的项链, “查询一个区间有多少个互不相同的数”吧（不知道是不是，目前蒟蒻只会这么一种，菜鸡实锤）。查询区间中有多少个互不相同的数的做法是用一个计数数组$cnt[]$来统计某个数出现的次数，再利用莫队这个巧妙的思想动态的维护cnt数组，进而计算有多少个互不相同的数(具体维护思路见代码).
对于$cf$这个题来说与$HH$的项链唯一的不同就是动态维护$cnt$数组的方式有一点小差异，再者就是需要离散化,数的范围稍大，其他部分几乎是相同的。(莫队不会怎么办，博主也只是刚会了个入门题，还讲不明白。👉戳我找大佬们学学)
莫队关键操纵：对查询的左端点分块，右端点单调处理

AC Coding:(HH的项链)

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 50010,M = 200010,S = 1000010;
int res[M],cnt[S],a[N];
int len;
struct node{
    int id,l,r;
}q[M];
int get(int x){
    return x / len;
}
bool cmp(node x,node y){
    int i = get(x.l),j = get(y.l);
    if(i != j) return i < j;
    else return x.r < y.r;
}
void add(int x,int& sum)
{
    if(!cnt[x]) sum++;
    cnt[x]++;
}
void del(int x,int& sum)
{
    cnt[x]--;
    if(!cnt[x]) sum--;
}
int main(){
    int n; scanf("%d",&n);
    for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
    int m; scanf("%d",&m);
    len = sqrt((double)n * n / m);
    for(int i = 1;i <= m;i++){
        int l,r; scanf("%d%d",&l,&r);
        q[i] = {i,l,r};
    }
    sort(q + 1,q + m + 1,cmp);
    int sum = 0;
    for(int k = 1,i = 1,j = 0;k <= m;k++){
        int l = q[k].l,r = q[k].r,id = q[k].id;
        while(i < l) del(a[i++],sum);
        while(i > l) add(a[--i],sum);
        while(j < r) add(a[++j],sum);
        while(j > r) del(a[j--],sum);
        res[id] = sum;
    }
    for(int i=1;i<=m;i++){
        printf("%d\\n",res[i]);
    }
    return 0;
}

AC Coding:(Little Elephant and Array)[莫队]

#include <cmath>
#include <cstdio>
#include <vector>
#include <string>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 100010;
struct node {
	int id, l, r;
}q[N];
int a[N], len, cnt[N], res[N];
vector<int> v;
int get(int x) {
	return x / len;
}
bool cmp(node x, node y) {
	int i = get(x.l), j = get(y.l);
	if (i != j) return i < j;
	else return x.r < y.r;
}
void add(int x, int& sum) {
	cnt[x]++;
	if (cnt[x] == v[x]) sum++;
	else if (cnt[x] == v[x] + 1) sum--;
}
void del(int x, int& sum) {
	if (cnt[x] == v[x]) sum--;
	else if (cnt[x] == v[x] + 1) sum++;
	cnt[x]--;
}
int main() {
	int n, m; scanf("%d%d", &n, &m);
	for (int i = 1;i <= n;i++) scanf("%d", &a[i]), v.push_back(a[i]);
	sort(v.begin(), v.end());
	v.erase(unique(v.begin(), v.end()), v.end());
	for (int i = 1;i <= n;i++) {
		a[i] = lower_bound(v.begin(), v.end(), a[i]) - v.begin();
	}
	len = sqrt((double)n * n / m);
	if (len == 0) len = n;
	for(int i = 1;i <= m;i++){
		int l, r; scanf("%d%d", &l, &r);
		q[i] = { i,l,r };
	}
	sort(q + 1, q + m + 1, cmp);
	int sum = 0;
	for (int k = 1, i = 1, j = 0;k <= m;k++) {
		int l = q[k].l, r = q[k].r, id = q[k].id;
		while (i < l) del(a[i++], sum);
		while (i > l) add(a[--i], sum);
		while (j < r) add(a[++j], sum);
		while (j > r) del(a[j--], sum);
		res[id] = sum;
	}
	for (int i = 1;i <= m;i++) {
		printf("%d\\n", res[i]);
	}
	return 0;
}

将上述两份代码对比查看，会发现确实大同小异👊。
二：暴力解法
首先来分析一下暴力解法的可行性。数组的最大长度$n\le 10^5$, 整个区间最多存在多少个互不相同的 $x$ 满足$cnt[x]=x$呐？最优秀的情况是 $1$ 个$1$，$2$个$2$，$3$个$3$… $k$个$k$的情况。可以根据等差数列求和公式稍作计算。当$k=450$，经计算，数组长度要有$101475$已经大于$10^5$，所以可以粗略的认为最多有 $450$ 个互不相同的数可能满足$cnt[x]=x$。

时间复杂度分析：对于建立并初始化前缀和数组的复杂度为O(450 * n)，查询时最多要遍历$450$个数,$1e5$次查询，$O(450\ast n)$.
所以时间复杂度大概是$O(4e7)$,在$1s$的时间内可以通过，所以是可行的。

然后利用前缀和的思想，分别将这 $450$ 个数在原数列中求前缀和。前缀和可以以 $O(1)$ 的时间复杂度得到某个区间某个值出现的个数。查询的时候，遍历这最多$450$个数的数组（注意：这450个数的数组不一定就是1,2,3,…,k。要根据这个数的出现次数和数值大小是否符合条件来判断的，出现次数大于等于数值大小就可以加入$st$数组<最多450个数的那个数组>行列），分别判断是否满足$cnt[x]=x$进行计数求和即可。

AC Coding:(Little Elephant and Array)[暴力]

#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 100010, M = 510;
int a[N], cnt[N], f[M][N], st[M];
int main() {
	int n, m; scanf("%d%d", &n, &m);
	for (int i = 1;i <= n;i++) {
		scanf("%d", &a[i]);
		if (a[i] <= n) cnt[a[i]]++;
	}
	int s = 0;
	for (int i = 1;i <= n;i++) {
		if (cnt[i] >= i) {
			st[++s] = i;
			for (int j = 1;j <= n;j++) {
				f[s][j] = f[s][j - 1] + (a[j] == i);
			}
		}
	Codeforces 220B-Little Elephant and Array-扫描线 & 树状数组

 CF587F Duff is Mad（AC自动机+树状数组+分块）
 分块思想基础莫队
 莫队算法小介绍——看似暴力的莫队算法
 BZOJ 3289 Mato的文件管理 | 莫队 树状数组
 CF 313 DIV2 B 树状数组