求斐波那契数列的第 N 项

Posted 2021-09-05 一朵花花

斐波那契数列介绍

斐波那契数列(Fibonacci sequence)，又称黄金分割数列，因数学家列昂纳多·斐波那契(Leonardoda Fibonacci) 以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34……在数学上，斐波纳契数列以如下被以递推的方法定义：F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>=3，n∈N*）在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用

斐波那契数列：1，1，2，3，5，8，13，21，34，55……

解决方法：

只讨论核心的代码，对于n的合法性判断，返回值是否溢出等问题不进行考虑
由：
F(1)=1，F(2)=1
F(n)=F(n-1)+F(n-2)（n>=3，n∈N*）

思路1：递归

public static int fib(int n){
	if(n==1 || n==2){
    	return 1;
	}
	return fib(n-1)+fib(n-2);
}

递归这种方式简单易懂，但开销大、容易产生栈溢出
斐波那契可以用来理解递归，但不适合使用递归运算，因为n越大，就会进行很多重复的运算，执行速度就会变慢

思路二：迭代：

public static int fib2(int n){
	int f1 = 1;
	int f2 = 1;
	int f3 = 1;
	for(int i = 3;i <= n;i++){
		f3 = f1 + f2;
	   	f1 = f2;
	   	f2 = f3;
	}
	return f3;
}

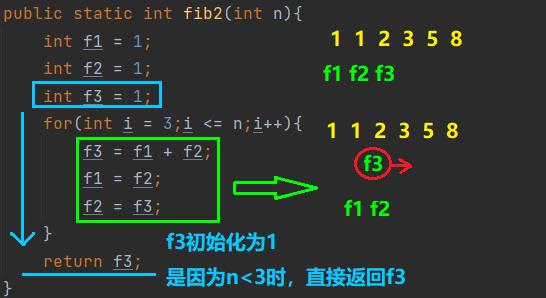
相比递归方式，更推荐使用迭代求解斐波那契问题。其唯一的缺点就是与递归法比可读性较弱