卐 4-3D图形的数学

Posted itzyjr

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了卐 4-3D图形的数学相关的知识，希望对你有一定的参考价值。

目录

Vectors（向量）

一个xyz三元组可以用一个向量来表示（事实上，对于数学上纯粹的心来说，一个位置实际上也是一个向量）。当涉及到操作三维几何体时，向量可能是需要理解的最重要的基础概念。这三个值（x、y和z）组合表示两个重要值：方向和幅值。

向量是OpenGL操作的基础，因此各种大小的向量都是GLSL中的一级类型，并被命名为vec3和vec4（分别表示三元素向量和四元素向量）。向量可以表示的第二个量是大小。向量的大小是向量的长度。对于x轴向量(1, 0, 0)，向量的长度是1。长度为1的向量称为单位向量。如果一个向量不是一个单位向量，我们想把它缩放成一个，我们称之为归一化。对向量进行归一化会对其进行缩放，使其长度变为1，然后称该向量为归一化向量。当我们只想表示一个方向而不是一个大小时，单位向量很重要。

此外，如果向量长度出现在我们将要使用的方程中，当这些长度为1时，它们会变得简单得多！幅值也很重要；例如，它可以告诉我们在给定的方向上需要走多远，我们需要离鳄鱼多远。向量（和矩阵）是3D图形中非常重要的概念，它们是GLSL语言（编写着色器的语言）中的头等公民。然而，在C++语言中，情况并非如此。为了允许你在C++程序中使用它们，vmath库，它包含可以表示类似于它们的GLSL对应的向量和矩阵的类。例如，vmath::vec3可以表示三分量浮点向量(x, y, z)，vmath::vec4可以表示四分量浮点向量(x, y, z, w)，依此类推。添加w坐标以使向量齐次(homogeneous)，但通常设置为1.0。稍后，x、y和z值可能会除以w，当它为1.0时，实际上只剩下xyz值。vmath中的类实际上是具有类型定义的模板类，用于表示常见类型，例如单精度和双精度浮点值以及有符号和无符号整数变量。

vmath::vec3与vmath::vec4的定义如下：

typedef Tvec3<float> vec3;
typedef Tvec4<float> vec4;

定义一个三元素向量简单如下：

vmath::vec3 vVector;

所有vmath类都定义了大量构造函数和复制运算符，这意味着您可以按如下方式声明和初始化向量：

vec3 vmath::vVertex1(0.0f, 0.0f, 1.0f);
vec4 vmath::vVertex2 = vec4(1.0f, 0.0f, 1.0f, 1.0f);
vec4 vmath::vVertex3(vVertex1, 1.0f);

vec3 vmath::vVerts[] = { vmath::vec3(-0.5f, 0.0f, 0.0f),
						 vmath::vec3(0.5f, 0.0f, 0.0f),
						 vmath::vec3(0.0f, 0.5f, 0.0f) };

vmath库还包括许多与数学相关的函数，并覆盖其类上的大多数运算符，以允许向量和矩阵进行加、减、乘、转置等操作。

在这里我们需要小心，不要过分地掩饰第四个w分量。大多数情况下，当您使用顶点位置指定几何体时，只需存储一个三分量顶点并将其发送到OpenGL即可。对于许多方向向量，例如曲面法线（垂直于用于照明计算的曲面的向量），三分量向量就足够了。但是，我们将很快深入研究矩阵世界，要变换3D顶点，必须将其乘以4×4变换矩阵。规则是你必须将一个四分量向量乘以一个4×4矩阵；如果你尝试使用一个4×4矩阵的三分量向量，鳄鱼会吃掉你！更多关于这一切意味着什么。本质上，如果你要对向量做你自己的矩阵运算，那么在很多情况下你可能需要四个分量向量。

Common Vector Operators（常用的向量操作）

向量的行为与加法、减法、一元求反等运算的预期相同。这些运算符执行每个分量的计算，并生成与其输入大小相同的向量。vmath向量类重载加法、减法和一元求反运算符以及其他几个运算符，以提供此类功能。

vmath::vec3 a(1.0f, 2.0f, 3.0f);
vmath::vec3 b(4.0f, 5.0f, 6.0f);
vmath::vec3 c;

c = a + b;
c = a - b;
c += b;
c = -c;

然而，在下面的小节中，从数学角度解释了更多关于向量的操作。它们在vmath库中也有实现，下面将对其进行概述。

Dot Product（点积）

设有两向量V1(x1,y1,z1)和V2(x2,y2,z2)，则有：
V1●V2 = |V1||V2|cosθ = x1x2 + y1y2 + z1z2
其中，θ是向量V1与V2的夹角。

vmath::vec3 a(...);
vmath::vec3 b(...);

float c = a.dot(b);
float d = dot(a, b);

一对单位向量之间的点积是一个值（介于−1.0和+1.0），表示它们之间夹角的余弦。一个稍微高级一点的函数vmath::angle实际上返回这个角度（弧度）。

float angle(const vmath::vec3& u, const vmath::vec3& v);
Cross Product（叉积）

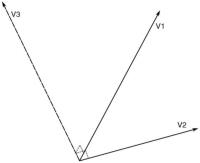
V1 × V2 = |V1||V2|sinθ×n = (y1z2 - z1y2, z1x2 - x1z2, x1y2 - y1x2)
其中，θ是向量V1与V2的夹角；n是一个单位向量，它的方向由V1和V2按右手定则产生（如下图中V3）。

vec3 a(...);
vec3 b(...);

vec3 c = a.cross(b);
vec3 d = cross(a, b);

叉积的应用很多，从寻找三角形的曲面法线到构造变换矩阵。

Length of a Vector（向量的长度）

设有向量V(x, y, z)，则它的长度为√(x2 + y2 + z2)。它的长度也等于√(V●V)。
vmath库中也包含计算这个长度的函数：

template <typename T, int len>
static inline T length(const vecN<T, len>& v) { ... }
Reflection and Refraction（反射和折射）


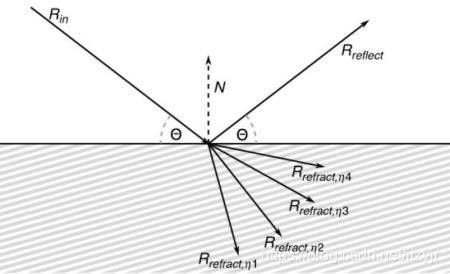
上图中，入射光线Rin，反射光线Rreflect，折射光线Rrefract。其中， η是折射因子。
反射光计算公式：Rreflect = Rin - (2N●Rin)N
折射光计算公式：
k = 1 - η2(1 - (N●R)2)
当k<0时，Rrefract = 0;
当k>=0时，Rrefract = ηR - (η(N●R) + √k)N
其中，R和N都是单位长度的向量。

vmath库有两个函数完成上述方程式，它们的源代码如下：

template <typename T, const int len>
static inline vecN<T,len> reflect(const vecN<T,len>& I, const vecN<T,len>& N) {
    return I - 2 * dot(N, I) * N;
}

template <typename T, const int len>
static inline vecN<T,len> refract(const vecN<T,len>& I, const vecN<T,S>& N, T eta) {
    T d = dot(N, I);
    T k = T(1) - eta * eta * (T(1) - d * d);
    if (k < 0.0)
        return vecN<T,N>(0);
    else
        return eta * I - (eta * d + sqrt(k)) * N;
}
Matrices（矩阵）

如果在空间中有一个点由x、y和z坐标表示，并且如果围绕某个任意点和方向旋转若干度，则需要知道该点的位置，就使用矩阵。为什么？因为新的x坐标不仅取决于旧的x坐标和其他旋转参数，而且还取决于y和z坐标是什么。变量和解之间的这种依赖关系正是矩阵擅长解决的问题。

我们可以把一些矩阵看作是列向量表。

矩阵可以相乘和相加，但也可以与向量和标量值相乘。将一个点（由向量表示）乘以一个矩阵（表示变换）得到一个新的变换点（另一个向量）。矩阵变换实际上不太难理解，对矩阵变换的理解是许多3D任务的基础。

vmath::mat2 m1;// 2×2 matrix
vmath::mat3 m2;// 3×3 matrix
vmath::mat4 m3;// 4×4 matrix

与GLSL中一样，vmath中的矩阵类定义了常见的运算符，如加法、减法、一元求反、乘法和除法，以及构造函数和关系运算符。同样，vmath中的矩阵类是使用模板构建的，包括单精度和双精度浮点以及有符号和无符号整数矩阵类型的类型定义。

Matrix Construction and Operators（矩阵的构建与操作）

对于一个4×4矩阵，OpenGL不是用一个二维数组存储矩阵的浮点值，而是用一个包含16个元素的一维数组表示。默认OpenGL是以列为主(column-major or column-primary)布局的。也就是说，对于一个4×4矩阵，前4个元素代表矩阵的第一列，接下来的4个元素代表矩阵的第二列，以此类推。

GLfloat matrix[16];// Nice OpenGL-friendly matrix
GLfloat matrix[4][4];// Not as convenient for OpenGL programmers

OpenGL可以使用第二种变体，但第一种变体更有效。

下面的数组代表上图的矩阵：

static const float A[] = {
	A00,A01,A02,A03, A10,A11,A12,A13,
	A20,A21,A22,A23, A30,A31,A32,A33
}

事实上，vmath库在内部将矩阵表示为它自己的向量类的数组，每个向量包含一列矩阵。

假设有矩阵A和B，以及向量V，则有：
A·(B·V) = (A·B)·V （矩阵乘法满足结合律）
我们可以用我们喜欢的任何方式将变换序列组合在一起，因为矩阵乘法是相联的，但是矩阵在乘法中出现的顺序很重要，因为矩阵乘法不满足交换律。

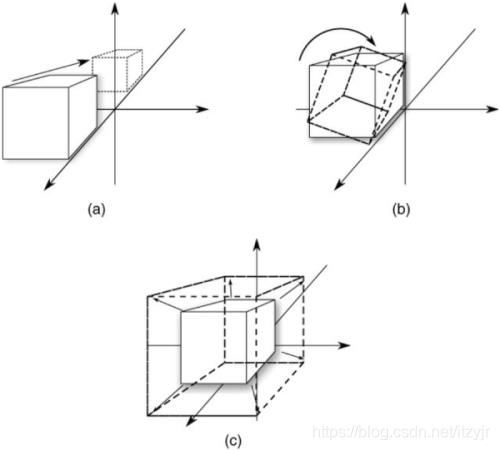
旋转与平移执行的先后顺序对物体的影响：

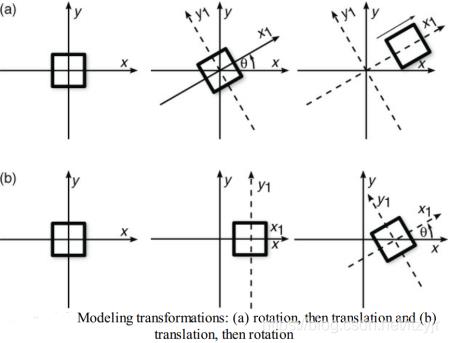
图(a)中正方形先绕z轴相对于原点旋转θ角，然后沿着旋转后的新x轴(即x1轴)平移，图(b)中相同的正方形先沿x轴平移，然后绕z轴相对于新原点旋转θ角。正方形的最终位置不同是因为每次变换都是相对于最后一次执行的变换执行的。在图(a)中，正方形首先相对于原点旋转。在图(b)中，正方形平移后，围绕新平移的原点进行旋转。

Understanding Transformations（理解变换）

仔细想想，大多数3D图形都不是真正的3D。我们使用3D概念和术语来描述事物的外观；然后这些3D数据被“挤压”到2D电脑屏幕上。我们称之为将三维数据压缩成二维数据投影的过程。每当我们想要描述顶点处理期间发生的变换类型（正交(orthographic)或透视(perspective)）时，我们都会提到投影(projection)，但投影只是OpenGL中发生的变换类型之一。变换还允许旋转对象；移动它们；甚至拉伸、收缩和扭曲它们。

Coordinate Spaces in OpenGL（OpenGL中的坐标空间）
坐标空间代表的含义
Model spacePositions relative to a local origin.Also sometimes known as object space.
World spacePositions relative to a global origin(i.e.,their location within the world).
View spacePositions relative to the viewer.Also sometimes called camera or eye space.
Clip spacePositions of vertices after projection into a nonlinear homogeneous coordinate.
Normalized device coordinate(NDC) spaceVertex coordinates are said to be in NDC after their clip space coordinates have been divided by their own w component.
Window spacePositions of vertices in pixels, relative to the origin of the window.
Object Coordinates（对象坐标系）

大多数顶点数据通常在对象空间(object space)（也称为模型空间(model space)）中开始使用。在对象空间中，顶点的位置相对于局部原点进行解释。考虑一个宇宙飞船模型。模型的起源可能会在某个合乎逻辑的地方，比如飞行器的鼻尖、重心或飞行员可能坐的位置。在3D建模程序中，返回原点并充分缩小应显示整个宇宙飞船。模型的原点通常是可以旋转模型以将其放置到新方向的点。将原点放置在远离模型的位置是没有意义的，因为围绕该点旋转对象将应用显著的平移和旋转。

World Coordinates（世界坐标系）

世界空间，它相对于固定的全局原点存储坐标的位置。继续宇宙飞船的类比，这可能是一个运动场或其他固定物体的中心，如附近的行星。一旦进入世界空间，所有对象都存在于一个公共框架中。通常，这是执行照明和物理计算的空间。

View Coordinates（视图坐标系）

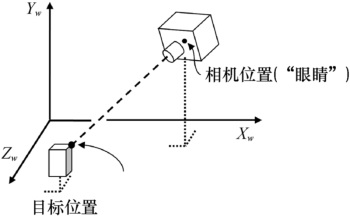
本章中的一个重要概念是视图坐标，通常也称为相机(camera)或眼睛(eye)坐标。视图坐标相对于观察者的位置（因此称为“相机”和“眼睛”），而不考虑可能发生的任何变换；你可以将它们视为“绝对”坐标。因此，眼睛坐标表示一个虚拟的固定坐标系，用作公共参考系。下图显示了两个视点的视图坐标系。在左侧，视图坐标表示为场景的观察者所看到的坐标（即，垂直于监视器）。在右侧，视图坐标系稍微旋转，以便更好地查看z轴的关系。从观察者的角度来看，正x和y分别指向右侧和上方。正z值从原点向用户移动，负z值从视点向屏幕移动。屏幕位于z坐标0处。

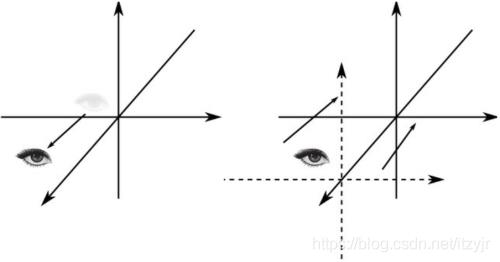
使用OpenGL在3D空间绘制时，使用笛卡尔坐标系。在没有任何变换的情况下，使用刚才描述的眼睛坐标系(eye coordinate system)。

Clip and Normalized Device Space（裁剪与归一化设备空间）

裁剪空间是OpenGL执行裁剪的坐标空间。当顶点着色器写入gl_Position时，该坐标被视为在裁剪空间(clip space)中。这始终是一个四维齐次坐标(four-dimensional homogenous coordinate)。退出剪辑空间后，顶点的所有四个组件将被w分量相除。显然，在此之后，w等于1.0。如果在此除法之前w不是1.0，则x、y和z分量将通过w的倒数进行有效缩放。这允许透视缩短和投影等效果。将除法结果视为在归一化设备坐标空间（NDC空间）中。显然，如果裁剪空间坐标的结果w分量为1.0，则裁剪空间和NDC空间将变得相同。

Coordinate Transformations（坐标转换）


如前所述，通过将坐标的向量表示乘以变换矩阵，可以将坐标从一个空间移动到另一个空间。变换用于操纵模型及其内的特定对象。这些变换将对象进行移动、旋转和缩放。上图说明了将应用于对象的三种最常见的建模转换。图(a)显示了平移，其中对象沿给定轴移动。图(b)显示了一个旋转，一个对象围绕其中一个轴旋转。最后，图©显示了缩放的效果，对象的尺寸增加或减少了指定的量。缩放可以不均匀地进行（不同的尺寸可以按不同的量进行缩放），因此可以使用缩放来拉伸和收缩对象。

这些标准变换中的每一个都可以表示为一个矩阵，你可以通过该矩阵乘以顶点坐标来计算变换后的位置。接下来小节讨论这些矩阵的构造，包括数学构造和使用vmath库中提供的函数。

The Identity Matrix（单位矩阵）

单位矩阵除斜对角线为1其余都为0。所有的单位矩阵都是平方的，如4×4。将顶点乘以单位矩阵等于将其乘以1。所有单位矩阵都是它本身的转置矩阵。

可以这样构建单位矩阵：

// Using a raw array:
GLfloat m1[] = { 1.0f, 0.0f, 0.0f, 0.0f,  // X Column
				 0.0f, 1.0f, 0.0f, 0.0f,  // Y Column
				 0.0f, 0.0f, 1.0f, 0.0f,  // Z Column
				 0.0f, 0.0f, 0.0f, 1.0f };// W Column
// Or using the vmath::mat4 constructor:
vmath::mat4 m2 { vmath::vec4(1.0f, 0.0f, 0.0f, 0.0f),  // X Column
				 vmath::vec4(0.0f, 1.0f, 0.0f, 0.0f),  // Y Column
				 vmath::vec4(0.0f, 0.0f, 1.0f, 0.0f),  // Z Column
				 vmath::vec4(0.0f, 0.0f, 0.0f, 1.0f) };// W Column
// use vmath library functions
vmath::mat2 m2 = vmath::mat2::identity();
vmath::mat3 m3 = vmath::mat3::identity();
vmath::mat4 m4 = vmath::mat4::identity();
The Translation Matrix（平移矩阵）


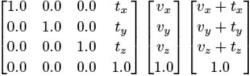
实际上，位置向量几乎总是使用四个分量编码，其中w分量为1.0，而方向向量要么简单地使用三个分量编码，要么使用四个分量编码，其中w为0。因此，将四分量方向向量乘以平移矩阵根本不会改变它。
vmath库包含两个函数，它们将使用三个单独的组件或三维向量为您构建4×4转换矩阵：

template <typename T>
static inline Tmat4<T> translate(T x, T y, T z) { ... }

template <typename T>
static inline Tmat4<T> translate(const vecN<T, 3>& v) { ... }
The Rotation Matrix（旋转矩阵）


可以将这三个矩阵相乘生成一个复合变换矩阵，然后在单个矩阵-向量相乘运算中围绕三个轴中的每个轴旋转给定的量。

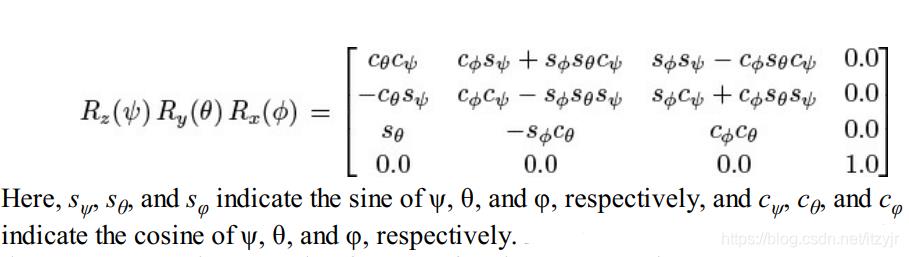
template <typename T>
static inline Tmat4<T> rotate(T angle_x, T angle_y, T angle_z);

template <typename T>
static inline Tmat4<T> rotate<T angle, T x, T y, T z);

template <typename T>
static inline Tmat4<T> rotate<T angle, const vecN<T, 3>& axis);

注意angle的单位是度数而非弧度。此函数在内部将度转换为弧度，因为与计算机不同，许多程序员更喜欢用度来思考。

Euler Angles（欧拉角）

欧拉角是一组表示空间方向的三个角。每个角度表示围绕定义帧的三个正交向量之一的旋转（例如，x、y和z轴）。如前所述，矩阵变换的执行顺序很重要，因为以不同的顺序执行某些变换（如旋转）将产生不同的结果。这是由于矩阵乘法的非交换性质(non-commutative nature)。

设定xyz-轴为参考系的参考轴。称xy-平面与XY-平面的相交为交点线，用英文字母（N）代表。zxz顺规的欧拉角可以静态地这样定义：

α 是x-轴与交点线的夹角，β 是z-轴与Z-轴的夹角，γ 是交点线与X-轴的夹角。

绕X轴旋转：

绕Y轴旋转：

绕Z轴旋转：

将方向表示为一组三个角度有一些优点。例如，这种类型的表示相当直观，如果你计划将角度连接到用户界面，这一点很重要。另一个好处是，插值角度、在每个点构造旋转矩阵以及在最终动画中看到平滑一致的运动非常简单。

然而，欧拉角也有一个严重的陷阱——万向锁(gimbal lock)。
当旋转一个角度使一个轴重新定向以与另一个轴对齐时，会发生万向节锁定。任何围绕两个现在共线的轴的进一步旋转都将导致模型的相同变换，从而从系统中移除自由度。因此，欧拉角不适合串联变换或累积旋转。
为了避免这种情况，我们的vmath::rotate函数能够获取旋转角度和旋转轴。当然，将三个旋转叠加在一起（x、y和z轴各一个）可以在必要时使用欧拉角，但最好使用角度轴表示旋转，或使用四元数表示变换并根据需要将其转换为矩阵。

The Scaling Matrix（缩放矩阵）

缩放变换通过按指定的因子沿三个轴扩展或收缩所有顶点来更改对象的大小。

// scale independently in the x,y,z
template <typename T>
static inline Tmat4<T> scale<T x, T y, T z) { ... }
// uses a vec3 vector rather than three separate parameters
template <typename T>
static inline Tmat4<T> scale<const Tvec3<T>& v) { ... }
// scale by the same amount x in all three dimensions
template <typename T>
static inline Tmat4<T> scale<T x) { ... }

例如，一个10×10×10立方体在x和z轴方向上绽放，如下图：

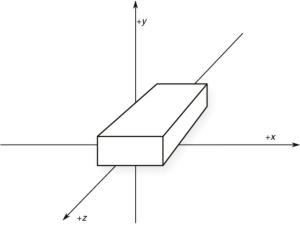
Concatenating Transformations（串联变换）

正如您所了解的，坐标变换可以用矩阵表示，向量从一个空间到另一个空间的变换涉及一个简单的矩阵-向量乘运算。乘以一系列矩阵可以应用一系列变换。在每次矩阵-向量相乘之后，不必存储中间向量。相反，首先将构成一组相关变换的所有矩阵相乘，生成一个表示整个变换序列的矩阵是可能的，并且通常更可取。然后，可以使用该矩阵将向量直接从源坐标空间转换到目标坐标空间。记住，顺序很重要。使用vmath或GLSL编写代码时，应始终将矩阵与向量相乘，并按倒序读取变换序列。例如，考虑下面的代码序列：

vmath::mat4 translation_matrix = vmath::translate(4.0f, 10.0f, -20.0f);
vmath::mat4 rotation_matrix = vmath::rotate(45.0f, vmath::vec3(0.0f, 1.0f, 0.0f));
vmath::vec4 input_vertex = vmath::mat4(....);
vmath::vec4 transformed_vertex = translation_matrix * rotation_matrix * input_vertex;

该代码首先将模型绕y轴旋转45°，然后将其在x轴上平移4个单位，在y轴上平移10个单位，在z轴上平移负20个单位。这会将模型放置在特定方向，然后将其移动到位。是先旋转，后平移。我们可以将此代码重写如下：

	vmath::mat4 translation_matrix = vmath::translate(4.0f, 10.0f, -20.0f);
	vmath::mat4 rotation_matrix = vmath::rotate(45.0f, vmath::vec3(0.0f, 1.0f, 0.0f));
	
	vmath::mat4 composite_matrix = translation_matrix * rotation_matrix;
	vmath::vec4 input_vertex = vmath::vec4(...);
	vmath::vec4 transformed_vertex = composite_matrix * input_vertex;// 先旋转，再平移
Quaternions（四元数）

四元数是一种四维量，在某些方面类似于复数。它有一个实部和三个虚部（与复数的一个虚部相比）。正如复数有一个虚部i一样，四元数有三个虚部i、j和k。数学上，四元数q表示为
q = (x + yi + zj + wk)
性质➊：i2 = j2 = k2 = ijk = -1。
性质➋：i = jk、j = ik、k = ji。

与复数一样，四元数的乘法是非交换的。四元数的加法和减法定义为简单的矢量加减法，各项按分量进行加减。其他函数（如一元否定和幅值）的行为也与四分量向量的预期相同。虽然四元数是一个四分量实体，但通常将四元数表示为实标量部分和三分量虚矢量部分。这种表述通常书面写作：q = (r, v)。

好的，很好，但这不是可怕的数学章节，对吗？这是关于计算机图形、OpenGL和所有有趣的东西。这就是四元数真正有用的地方。回想一下，我们的旋转函数以一个角度和一个轴为中心旋转。
我们可以将这两个量表示为四元数，在实部填充角度，在向量部填充轴，得到一个表示绕任意轴旋转的四元数。
旋转序列可以由一系列四元数相乘表示，生成一个四元数，一次编码整个批次。虽然可以生成一组表示围绕各个笛卡尔轴旋转的矩阵，然后将它们相乘，这种方法容易受到万向节锁的影响。如果对一系列四元数执行相同的操作，则万向节锁定不会发生。为了便于编写代码，vmath包括vmath::quaternion类，该类实现了这里描述的大部分功能。

The Model-View Transform（模型-视图变换）

在一个简单的OpenGL应用程序中，最常见的转换之一是将模型从模型空间(model space)转换到视图空间(view space)，以便对其进行渲染。实际上，我们首先将模型移动到世界空间（即相对于世界原点放置），然后再从那里移动到视图空间（相对于观察者放置）。这个过程确定了场景的有利位置。默认情况下，透视投影中的观察点位于原点（0,0,0），看向负z轴（进入监视器或屏幕）。该观察点相对于眼睛坐标系(eye coordinate system)移动，以提供特定的有利位置。当观察点位于原点时，如在透视投影中，使用正z值绘制的对象位于观察者后面。然而，在正交投影中，假定观察者在正z轴上无限远，并且可以看到视体(viewing volume)内的一切。

由于此变换将顶点从模型空间（有时也称为对象空间）直接带入视图空间，并有效地绕过世界空间，因此通常称为模型-视图变换，对此变换进行编码的矩阵称为模型-视图矩阵。

模型变换实质上是将对象放置到世界空间中。每个对象都可能有自己的模型变换，通常由一系列缩放、旋转和平移操作组成。将模型空间中顶点的位置乘以模型变换的结果是世界空间中的一组位置。这种转换有时被称为模型-世界转换(model-world transform)。

视图转换允许您将观察点放置在任意位置，并朝任意方向观察。确定查看变换类似于将摄影机放置并指向场景。在总体方案中，必须在任何其他建模转换之前应用视图转换。原因是它似乎相对于眼睛坐标系移动了当前工作坐标系。然后，所有后续变换都基于新修改的坐标系进行。将坐标从世界空间移动到视图空间的变换有时称为世界-视图变换(world-view transform)。

通过将模型-世界和世界-视图变换矩阵相乘，将它们连接在一起，得到模型-视图矩阵（即，从模型到视图空间获取坐标的矩阵）。这样做有一些好处。首先，场景中可能有许多模型，每个模型中都有许多顶点。如前所述，使用单复合变换将模型移动到视图空间比先将其移动到世界空间，然后再移动到视图空间更有效。第二个优势更多地与单精度浮点数字的数值精度有关：世界可能很大，在世界空间中执行的计算将具有不同的精度，具体取决于顶点离世界原点的距离。但是，如果在视图空间中执行相同的计算，则精度取决于顶点离观察者的距离，这可能是您想要的——对靠近观察者的对象应用了大量的精度，但牺牲了距离观察者很远的精度。

The Lookat Matrix（Lookat矩阵）

如果你在一个已知的位置有一个有利的位置，并且你想看一个东西，你会希望把你的虚拟相机放在那个位置，然后把它指向正确的方向。要正确定位相机，您还需要知道它向上的方向；否则，相机可能会绕着它的前向轴旋转，即使从技术上讲它仍然指向正确的方向，这几乎肯定不是你想要的。因此，给定一个原点、一个感兴趣点和一个我们认为要上升的方向，我们想要构造一系列变换，理想地烘烤成一个矩阵，这将表示一个旋转，它将指向一个摄像机在正确的方向上，一个将原点移动到摄像机中心的平移。该矩阵称为lookat矩阵(lookat matrix)，可仅使用本章迄今为止所述的数学知识构建。

首先，我们知两个位置相减会得到一个向量，这个向量会将一个点从第一个位置移动到第二个位置，而对向量结果进行归一化会得到它的方向。因此，如果我们取一个关注点的坐标，从中减去我们相机的位置，然后归一化得到的向量，我们就有了一个新的向量，表示从相机到关注点的视角方向。我们称之为前向向量(forward vector)。

接下来，我们知道，如果我们取两个向量的叉积，我们将得到与两个输入向量正交（成直角）的第三个向量。我们有两个矢量，我们刚才计算的前向矢量(forward vector)，和向上矢量(up vector)，它代表我们认为向上的方向。取这两个向量的叉积，得到第三个向量，该向量与它们中的每一个向量正交，并且相对于我们的相机指向侧面。我们称之为侧向向量(sideways vector)。然而，上方向向量和前方向向量不一定相互正交，我们需要第三个正交向量来构造旋转矩阵。为了得到这个向量，我们可以简单地再次应用相同的过程，取前向向量和侧向向量的叉积，得到第三个向量，这第三个向量与前向向量和侧向向量正交，表示相对于相机的上方向(up)。

这三个向量具有单位长度，并且彼此正交，因此它们形成一组正交基向量并表示我们的视图框架。给定这三个向量，我们可以构造一个旋转矩阵，它将在标准笛卡尔基础上取一个点，并将其移动到相机的基础上。在下面的数学中，e是眼睛（或相机）的位置，p是关注点，u是上方向向量。

首先，构造我们的前向向量f：
f = (p - e) / |p - e|
然后，构造侧向向量s：
s = f×u
在相机参考中构造一个新的上方向向量u′：
u′ = s×f
最后，构造一个旋转矩阵，表示重新定向到我们新构造的正交基中：

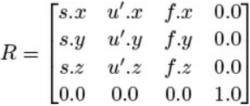
要将对象转换为摄影机的帧，不仅需要正确确定所有对象的方向，还需要将原点移动到摄影机的位置。我们通过简单地将结果向量转换为相机位置的负数来实现这一点。还记得平移矩阵是如何通过将偏移量放入矩阵最右边的列中来构造的吗？我们也可以在这里这样做：

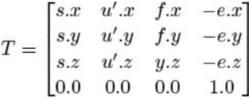
终于，我们得到lookat矩阵，就是上面的矩阵T。

template <typename T>
static inline Tmat4<T> lookat(const vecN<T,3>& eye, const vecN<T,3>& center, const vecN<T,3>& up) { ... }

由vmath::lookat函数生成的矩阵可以用作相机矩阵的基础——表示相机位置和方向的矩阵。换句话说，这可以是你的视图矩阵。

Projection Transformations（投影变换）

投影变换将在模型-视图变换后应用于顶点。该投影实际上定义了视体并建立了剪裁平面。剪裁平面是三维空间中的平面方程，OpenGL使用它来确定观察者是否可以看到几何体。更具体地说，投影变换指定如何将完成的场景（完成所有建模后）投影到屏幕上的最终图像。你将了解有关正交投影(orthographic)和透视投影(perspective)两种类型的详细信息。

在正交或平行投影中，所有多边形都以指定的相对尺寸精确地绘制在屏幕上。直线和多边形使用平行线直接映射到2D屏幕，这意味着无论某物离屏幕有多远，它仍然绘制为相同大小，只是在屏幕上展平。这种类型的投影通常用于渲染二维图像，如蓝图(blueprints)中的正面、顶部和侧面立面，或二维图形（如文本或屏幕菜单）。

透视投影显示的场景更多的是真实生活中的场景，而不是蓝图。透视投影的特点是缩短(foreshortening)，这使得远处的物体看起来比同样大小的附近物体小。三维空间中可能平行的线并不总是与观察者平行。例如，对于铁路轨道，轨道是平行的，但使用透视投影，它们似乎在某个遥远的点会聚。透视投影的好处是，你不必知道直线在哪里会聚，也不必知道远处的物体有多小。您只需使用模型-视图变换指定场景，然后应用透视投影矩阵。线性代数为你带来了所有的魔力。

下图比较了两个不同场景上的正交投影和透视投影。

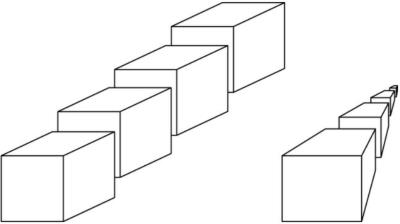
正如你在左侧显示的正交投影中所看到的，立方体在远离查看器时，其大小似乎不会发生变化。然而，在右侧显示的透视投影中，立方体随着距离观察者越来越远而变得越来越小。

正交投影最常用于二维绘图目的，其中需要像素和绘图单位之间的精确对应。您可以将它们用于原理图布局、文本或二维图形应用程序。如果渲染深度与距视点的距离相比具有非常小的深度，则也可以使用正交投影进行三维渲染。透视投影用于渲染包含需要应用缩短的开阔空间或对象的场景。在大多数情况下，透视投影是典型的三维图形。事实上，用正交投影观察3D对象可能会有点令人不安。

Perspective Matrices（透视矩阵）

一旦顶点在视图空间中，我们需要将它们放入裁剪空间，我们可以通过应用投影矩阵来实现这一点，投影矩阵可以表示透视投影或正交投影（或其他投影）。常用的透视矩阵是平截头体矩阵。平截头体矩阵是一种投影矩阵，它生成透视投影，使得裁剪空间的形状为矩形平截头体，即截断的矩形棱锥体。其参数是到近平面和远平面的距离以及左、右、上和下剪裁平面的世界空间坐标。平截体矩阵采用以下形式：

static inline mat4 frustum(float left, float right, float bottom, float top, float n, float f) { ... }

构造透视矩阵的另一种常用方法是直接将视野(field of view)指定为角度(FOV角)（可能以度为单位）、纵横比（通常通过将窗口的宽度除以其高度得出）以及近平面和远平面的视图空间位置。这在某种程度上更易于指定，并且只生成对称的视锥(symmetric frustra)。然而，这几乎总是你想要的。

static inline mat4 perspective(float fovy, float aspect, float n, float f) { ... }
Orthographic Matrices（正交矩阵）

如果希望对场景使用正交投影，则可以构造（稍微简单一些的）正交投影矩阵。正交投影矩阵只是将视图空间坐标线性映射到裁剪空间坐标的缩放矩阵。构造正交投影矩阵的参数是场景边界的视图空间中的左、右、上和下坐标，以及近平面和远平面的位置。

static inline mat4 ortho(float left, float right, float bottom, float top, float near, float far) { ... }
Interpolation,Lines,Curves,and Splines（插值、直线、曲线和样条曲线）


D = B - A
P = A + tD = A + t(B - A) = (1 - t)A + tB
如果t在0.0和1.0之间，那么P将在A和B之间结束。超出此范围的t值会将P推离线的末端。你们应该可以看到，通过平滑地改变t，我们可以将点P从A移到B，然后再移回来。这被称为线性插值(linear iterpolation)。A和B（和P）的值可以有任意数量的维度。例如，它们可以是标量值；二维值，如图形上的点；三维值，如三维空间中的坐标、颜色等；或者更高维度的数量，例如矩阵、数组，甚至整个图像。在许多情况下，线性插值没有多大意义（例如，两个矩阵之间的线性插值通常不会产生有意义的结果），但角度、位置和其他坐标通常可以安全地插值。

线性插值是图形中的一种常见操作，GLSL包括一个专门用于此目的的内置函数，mix:

vec4 mix(vec4 A, vec4 B, float t);

mix函数有几个版本，将向量或标量的不同维数作为A和B输入，并将标量或匹配向量作为t输入。

Curves（曲线）

如果我们只想沿着两点之间的直线移动所有东西，那么这就足够了。但是，在现实世界中，对象以平滑曲线移动，并平滑地加速和减速。曲线可以由三个或更多控制点表示。对于大多数曲线，有三个以上的控制点，其中两个形成端点；其他

以上是关于卐 4-3D图形的数学的主要内容，如果未能解决你的问题，请参考以下文章

卐 3-管线

C# 如何改变控制台输出字体颜色

Android片段布局完成膨胀

虎书学习笔记5：图形学基础数学（三维隐式曲面三维参数曲面）

text 数学片段

使用底图作为Python GUI中的图形