POJ2559 acwing131 Largest Rectangle in a Histogram [单调栈]

Posted 2021-09-05 布图

题目

直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

例如，图例左侧显示了由高度为 2,1,4,5,1,3,32,1,4,5,1,3,3 的矩形组成的直方图，矩形的宽度都为 11：

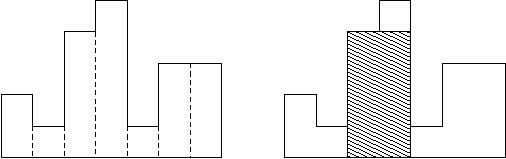
通常，直方图用于表示离散分布，例如，文本中字符的频率。

现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

输入格式

输入包含几个测试用例。

每个测试用例占据一行，用以描述一个直方图，并以整数 nn 开始，表示组成直方图的矩形数目。

然后跟随 nn 个整数 h1，…，hnh1，…，hn。

这些数字以从左到右的顺序表示直方图的各个矩形的高度。

每个矩形的宽度为 11。

同行数字用空格隔开。

当输入用例为 n=0n=0 时，结束输入，且该用例不用考虑。

输出格式

对于每一个测试用例，输出一个整数，代表指定直方图中最大矩形的区域面积。

每个数据占一行。

请注意，此矩形必须在公共基线处对齐。

数据范围

1≤n≤1000001≤n≤100000,
0≤hi≤10000000000≤hi≤1000000000

输入样例：

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

输出样例：

8
4000

难度：简单
时/空限制：1s / 64MB
总通过数：4899
总尝试数：11047
来源：《算法竞赛进阶指南》
算法标签

代码

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <string>
#include <iostream>
#include <sstream>
#include <set>
#include <map>
#include <queue>
#include <bitset>
#include <vector>
#include <limits.h>
#include <assert.h>
#include <functional>
#include <numeric>
#include <ctime>
//#include <ext/pb_ds/assoc_container.hpp>
//#include <ext/pb_ds/tree_policy.hpp>
#define pb          push_back
#define ppb         pop_back
#define lbnd        lower_bound
#define ubnd        upper_bound
#define endl        '\\n'
#define mll         map<ll,ll>
#define msl         map<string,ll>
#define mls         map<ll, string>
#define rep(i,a,b)  for(ll i=a;i<b;i++)
#define repr(i,a,b) for(ll i=b-1;i>=a;i--)
#define trav(a, x)  for(auto& a : x)
#define pll         pair<ll,ll>
#define vl          vector<ll>
#define vll         vector<pair<ll, ll>>
#define vs          vector<string>
#define all(a)      (a).begin(),(a).end()
#define F           first
#define S           second
#define sz(x)       (ll)x.size()
#define hell        1000000007
#define DEBUG       cerr<<"/n>>>I'm Here<<</n"<<endl;
#define display(x)  trav(a,x) cout<<a<<" ";cout<<endl;
#define what_is(x)  cerr << #x << " is " << x << endl;
#define ini(a)      memset(a,0,sizeof(a))
#define ini2(a,b)   memset(a,b,sizeof(a))
#define rep(i,a,b)  for(int i=a;i<=b;i++)
#define case        ll T;cin>>T;for(ll Q=1;Q<=T;Q++)
#define lowbit(x)   x&(-x)
#define pr          printf
#define sc          scanf
#define _           0
#define ordered_set tree<ll, null_type,less<ll>, rb_tree_tag,tree_order_statistics_node_update>
#define FAST ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define DBG(x) \\
    (void)(cout << "L" << __LINE__ \\
    << ": " << #x << " = " << (x) << '\\n')
#define TIE \\
    cin.tie(0);cout.tie(0);\\
    ios::sync_with_stdio(false);
//#define long long int

//using namespace __gnu_pbds;

using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const double PI    = acos(-1.0);
const double eps   = 1e-6;
const int    INF   = 0x3f3f3f3f;
const ll     LLINF = 0x3f3f3f3f3f3f3f3f;
const int    maxn  = 1e5+10;
const ll     N     = 5;

typedef struct LNode{
    int coef,index;
    struct LNode *next;
}LNode,*LinkList;

struct SegmentTree{
	int l, r;
	int dat;
}t[N*4];

bool cmp(int a,int b){
	return a>b;
}

ll st [maxn];
ll arr[maxn];
ll wid[maxn];
	
void solve(){
	ll n;
	while (cin>>n) {
		ll cnt = 0, ans = -LLINF;
		if (n==0) return ;
		for (ll i=1; i<=n; i++) {
			cin>>arr[i];
		}
		arr[0] = arr[n+1] = -1;
		for (ll i=1; i<=n+1; i++) {
			if (cnt==0 || st[cnt-1] <= arr[i]) {//大于就入栈 
				st[cnt] = arr[i];//入栈 
				wid[cnt++] = 1;//宽度为1 
			} else {
				ll width = 0;//记录宽度 
				while (cnt>=0 && st[cnt-1] > arr[i]) {//计算前面的,直到栈顶小于等于该元素 
					width += wid[cnt-1];
					ans = max(ans, width*st[cnt-1]);//把每次的最大值遍历一遍 
					cnt--;//出栈 
				}
				st[cnt] = arr[i];//最后把该值入栈 
				wid[cnt++] = width+1;//更新宽度 
			}
		}
		cout<<ans<<endl;
	}
	
}

int main()
{
//	TIE;
//    #ifndef ONLINE_JUDGE
//    freopen ("input.txt","r",stdin);
//    #else
//    #endif
	solve();
//    case{solve();}
//    case{cout<<"Case "<<Q<<":"<<endl;solve();}
	return ~~(0^_^0);
}