Pytorch—万字入门SSD物体检测

Posted 2021-09-05 Eloik

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Pytorch—万字入门SSD物体检测相关的知识，希望对你有一定的参考价值。

前言

由于初入物体检测领域，我在学习SSD模型的时候遇到了很多的困难。一部分困难在于相关概念不清楚，专业词汇不知其意，相关文章不知所云；另一部分困难在于网上大部分文章要么只是简要介绍了SSD的总体原理，要么就是直接实战。SSD作者的论文也已看过，但是看的还是蒙圈蒙圈的。
我决定通过代码来了解其原理，首先参考了https://blog.csdn.net/weixin_44791964/article/details/104981486这篇文章的代码，但是并没有看懂（I’m too vegetable），然后去GitHub上去搜了一下，一页的搜索结果恰好点到了这个项目，https://github.com/sgrvinod/a-PyTorch-Tutorial-to-Object-Detection，于是，困扰我的一些问题终于看到了通路，这个作者对SSD关键的介绍非常清晰，代码也是一目了然。我决定在其中添加自己的理解，并对代码进行一些修改加解读，一方面帮助我更清楚的理解物体检测，一方面帮助像我一样的人入门物体检测。

概念

在实现模型之前，我们需要对一些常见概念词进行了解，后面大多数直接使用原英文单词说明，当然这里只是粗略的解释，是为了让你明白一些专业的术语，即使不理解其含义也并无大碍，在文章中途会结合代码进行更详细的解释。

Object Detection（物体检测）：懂得都懂
Single-Shot Detection（单步检测） ：早期的物体检测模型结构由两部分组成——一个region proposal network（区域建议网络）用来定位物体的位置，一个classifier（分类器）检测建议区域中物体的类别。这种分两步的模型很消耗算力，因此它们不适合用来做实时检测。单步检测模型将定位与分类封装在一次前向计算中，大大提高了检测速度，同时使得模型可以部署在轻量级硬件中。
Multiscale Feature Maps（多尺度特征图）：在图像分类任务中，我们根据最后一个卷积特征图（原始图像的最小也是最深的表达）进行预测。在物体检测任务中，中间的卷积特征图也非常有用，因为它们代表了原图像不同的缩放比例。因此，由于这些特征图自带缩放，一个固定大小的 filter（滤波器，也就是卷积中的卷积核）在不同的特征图上进行运算，就能够检测到各种大小的物体。
Priors（先验，以后只用英文单词）：这些 priors boxes（先验框）是在特定尺度的特征图上特定位置预先生成的 boxes（框），它们有特定的 aspect ratios（长宽比）和 scales（比例）。它们是精心选择的，用来匹配数据集中物体边界框（也叫 ground truths，这个词经常使用，记住它指的就是数据集中物体的真实标记框）的特征。
Multibox（实在不好翻译，在后面会有更加清楚的解释）：这是一项将预测物体边界框的任务转变为一个回归任务的技术，被检测物体的坐标将被回归到对应它的真实框的坐标。同时，对每一个预测框，会生成每一个类别的分数（框内的物体就属于分数最高的类别，这与图像分类任务一样）。priors（先验框） 可以作为可行的起点，因为它们是以 ground truths（真实框） 为依据的。因此将会有和priors一样多的预测框，但是大多数预测框不包含物体。
Hard Negative Mining（硬负采样）：它明确指明了模型选择预测最错误的假正例（即背景类），强迫模型通过这些样例进行学习。换句话说，我们只对那些最难正确识别的错误因素进行采样。在物体检测任务中，我们生成的先验框非常多（SSD中为8732个），不难想象这些 priors 绝大部分是不包含任何物体的，因此，对于分类任务，这导致了严重的样本不均衡，会使预测结果变得非常差，硬负采样只让模型学习最难被识别的背景类，这极大减少了负样本的数量，有利于平衡正负样本。
Non-Maximum Suppression（NMS，非极大抑制）：我们生成的 priors 最终预测时将会有一部分重叠程度非常大的预测框，这些重叠程度大的预测框可能预测的是同一个物体， NMS（非极大抑制）是一种消除冗余预测的方法，它将删除除预测最高分之外其他所有重叠程度大的预测框。

综述

在本部分，我将介绍SSD模型的概述。在我们继续进行下去的过程中，你应该会注意到相当多的工程设计导致了SSD非常特殊的结构和方法。如果你觉得有些步骤和方法显得十分不自然（具有明显的人为倾向，没有理论支持，或者难以理解为何这样做），不用担心，请记住，它是建立在这个领域多年的研究（通常是经验性的）上的。

Bounding box（边界框）

bounding box（边界框）就是包裹着一个物体的盒子，代表着这个物体的界限。在本教程中我们只会遇到两种类型——普通框（不含物体的框）和边界框。但是所有的框都是在图像上表示的，我们需要能够测量它们的位置、形状、大小和其他属性。

Boundary coordinates（边界坐标）

表示一个框的最明显的方法就是使用构成其边界的线的像素坐标。一个框的边界坐标很简单的表示为 $x_{min}, y_{min}, x_{max}, y_{max})$ ，也就是框的左上角和右下角坐标，如下图所示。

但是如果我们不知道图像的实际大小，这种坐标将毫无意义。更好的方法是将所有坐标表示为比例的形式，即将 $x$ 坐标值除以图像的宽度，将 $y$ 坐标值除以图像的高度。

这样，如上图所示，坐标值将被缩放到 $[0, 1]$ 之间，即使我们不知道图片真实的大小，也可以知道框的位置。现在坐标是大小不变的，所有图片上的所有框都以相同比例测量。

Center-Size coordinates（中心坐标）

这是表示框的位置和尺寸的一种更明确的方法。

一个框的中心坐标形式为 $c_x, c_y, w, h)$ ，其中各个字母的含义在上图中可以非常明显的看出，这里就不再进行赘述，需要注意的是这里的所有坐标都进行了上述的缩放。
在这个代码中，你会发现我们通常使用两种坐标系统，这取决于它们对任务的适用性，并且总是以比例分数形式出现的（即进行了缩放）。

两种坐标系统的转换

边界坐标转中心坐标
从上面的介绍中，我们可以非常清楚的得出：
$c_x = \\frac{x_{min} + x_{max}}{2} ,\\quad c_y = \\frac{y_{min} + y_{max}}{2}$
$x_{max} - x_{min} , \\quad h = y_{max} - y_{min}$

def xy_to_cxcy(xy):
    """
    边界坐标转中心坐标
    :param xy: 一个shape为 [n,4]的tensor，表示n个边界坐标
    :return: 一个shape为 [n,4]的tensor，表示转换后的n个中心坐标
    """
    return torch.cat([
        (xy[:, 2:] + xy[:, :2]) / 2,  # cx, cy
        xy[:, 2:] - xy[:, :2]  # w, h
    ], dim=1)

中心坐标转边界坐标
同样，可以非常明显地看出如下关系：
$x_{min} = c_x - \\frac{w}{2}, \\quad y_{min} = c_y - \\frac{h}{2}$
$x_{max} = c_x + \\frac{w}{2} , \\quad y_{max} = c_y + \\frac{h}{2}$

def cxcy_to_xy(cxcy):
    """
    中心坐标转边界坐标
    :param cxcy: 一个shape为 [n,4]的tensor，表示n个中心坐标
    :return: 一个shape为 [n,4]的tensor，表示转换后的n个边界坐标
    """
    return torch.cat([
        cxcy[:, :2] - (cxcy[:, 2:] / 2),  # x_min, y_min
        cxcy[:, :2] + (cxcy[:, 2:] / 2)  # x_max, y_max
    ], dim=1)

Jaccard Index（IoU，重叠程度）

Jaccard Index（Jaccard 系数）或称作 Jaccard Overlap（Jaccard重叠）或称作 Intersection-over-Union（IoU，交并比），测量了两个框的重叠程度，这个指标可以反映预测框与真实框的接近程度，在计算loss和进行NMS（非极大抑制）时会用到。如下图所示。

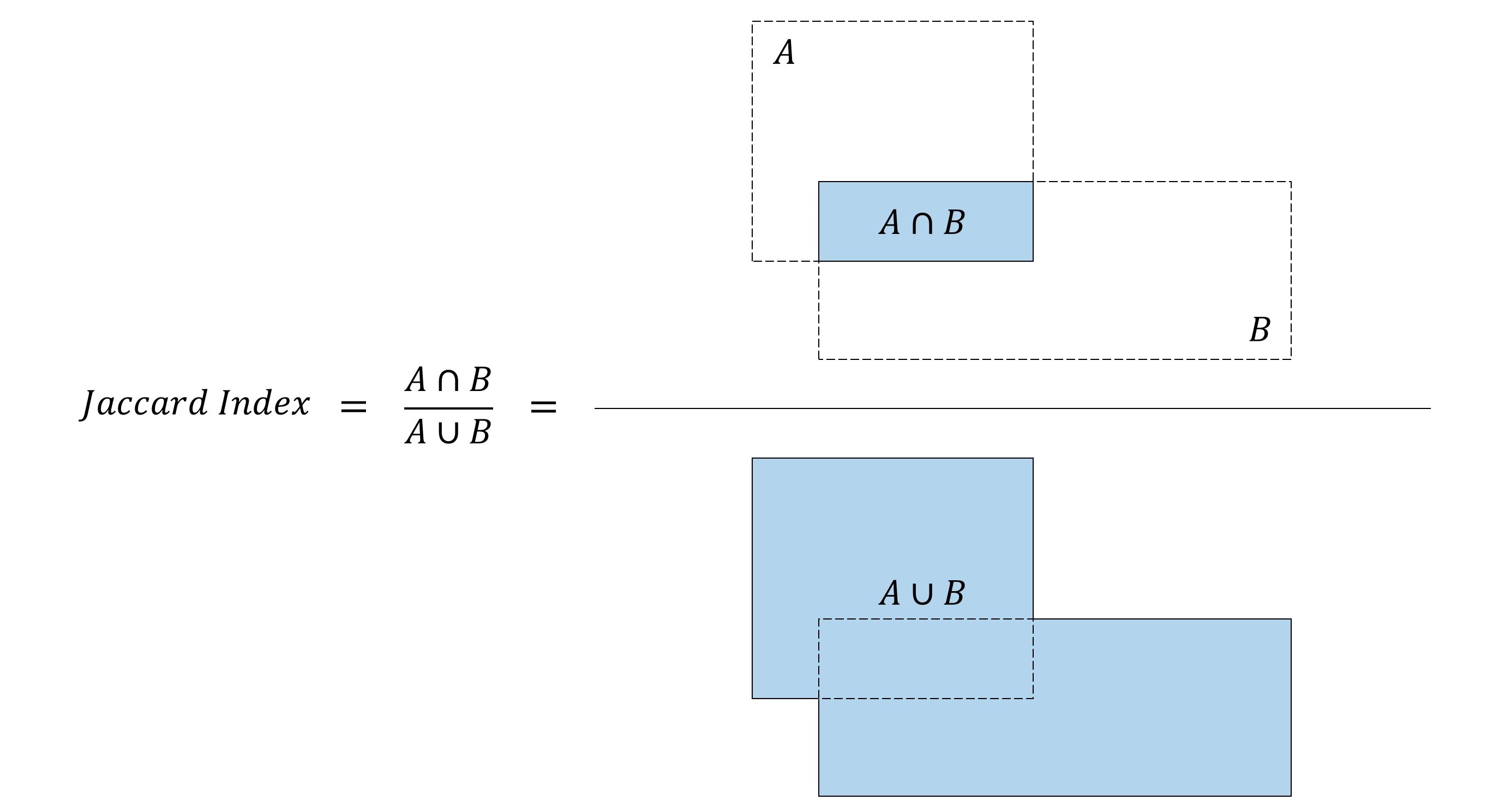
显然，Jaccard系数的取值在 $[0, 1]$ 之间，取值为0时，说明两个框的交集为0，也就是两个框没有重叠；取值为1时，说明两个框的交集与并集相同，也就是两个框完全重叠。
Jaccard系数的代码实现可能不能很好的理解，我们需要求两个量，一个是交集面积，一个是并集面积，而且 $并集面积 = 框 A 的面积 + 框 B 的面积 - 交集面积$ ，框A和框B的面积都非常容易计算，因此我们将目光放在交集面积的计算上。考虑一些常见的交集方式，如下图，绿色点表示交集区域左上角，蓝色点表示交集区域右下角。

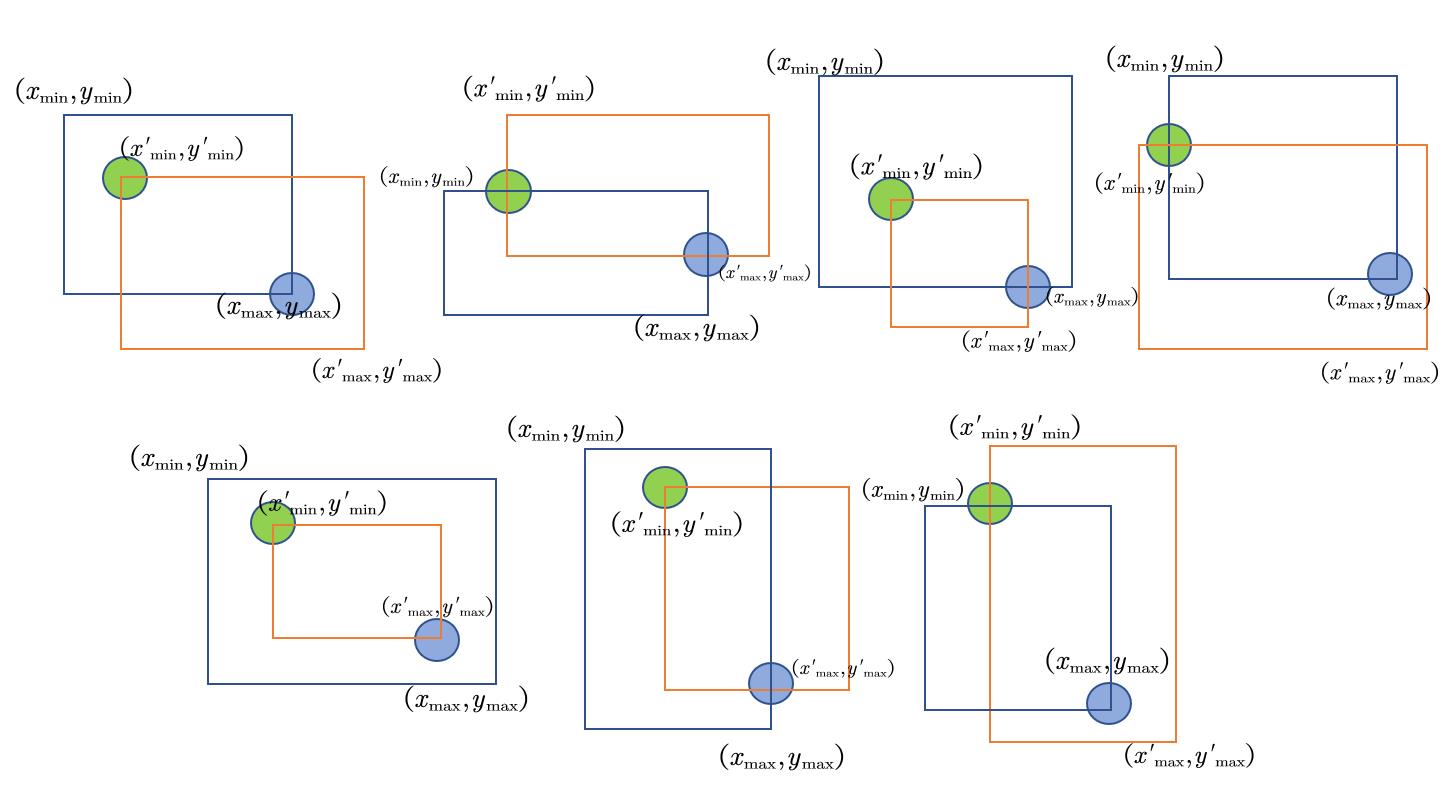
从上图中，我们可以看出，交集的区域都可以用两个点表示，这正是交集区域的边界坐标，整个交集区域的边界坐标可以表示为： $I_{x_{\\min}}, I_{y_{\\min}}, I_{x_{\\max}}, I_{y_{\\max}})$