openGauss数据库源码解析系列文章—— SQL引擎源解析

Posted Gauss松鼠会

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了openGauss数据库源码解析系列文章—— SQL引擎源解析相关的知识，希望对你有一定的参考价值。

上一篇文章介绍了SQL引擎源解析中“6.1 概述”及“6.2 SQL解析”的精彩内容，本篇我们开启“6.3 查询优化”及“6.4 小结”的相关内容的介绍。

6.3 查询优化

openGauss数据库的查询优化过程功能比较明晰，从源代码组织的角度来看，相关代码分布在不同的目录下，如表6-6所示。

表6-6 查询优化模块说明

模块

目录

说明

查询重写

src/gausskernel/optimizer/prep

主要包括子查询优化、谓词化简及正则化、谓词传递闭包等查询重写优化技术

统计信息

src/gausskernel/optimizer/commands/analyze.cpp

生成各种类型的统计信息，供选择率估算、行数估算、代价估算使用

代价估算

src/common/backend/utils/adt/selfuncs.cpp

src/gausskernel/optimizer/path/costsize.cpp

进行选择率估算、行数估算、代价估算

物理路径

src/gausskernel/optimizer/path

生成物理路径

动态规划

src/gausskernel/optimizer/plan

通过动态规划方法对物理路径进行搜索

遗传算法

src/gausskernel/optimizer/geqo

通过遗传算法对物理路径进行搜索

6.3.1 查询重写

SQL语言是丰富多样的，非常的灵活，不同的开发人员依据经验的不同，手写的SQL语句也是各式各样，另外还可以通过工具自动生成。SQL语言是一种描述性语言，数据库的使用者只是描述了想要的结果，而不关心数据的具体获取方式，输入数据库的SQL语言很难做到是以最优形式表示的，往往隐含了一些冗余信息，这些信息可以被挖掘用来生成更加高效的SQL语句。查询重写就是把用户输入的SQL语句转换为更高效的等价SQL，查询重写遵循两个基本原则。
（1） 等价性：原语句和重写后的语句，输出结果相同。
（2） 高效性：重写后的语句，比原语句在执行时间和资源使用上更高效。
查询重写主要是基于关系代数式的等价变换，关系代数的变换通常满足交换律、结合律、分配率、串接率等，如表6-7所示。

表6-7 关系代数等价变换

等价变换

内容

交换律

A × B == B × A

A ⨝B == B ⨝ A

A ⨝F B == B ⨝F A ……其中F是连接条件

Π p(σF (B)) == σF (Π p(B)) ……其中F∈p

结合律

(A × B) × C==A × (B × C)

(A ⨝ B) ⨝ C==A ⨝ (B ⨝ C)

(A ⨝F1 B) ⨝F2 C==A ⨝F1 (B ⨝F2 C) …… F1和F2是连接条件

分配律

σF(A × B) == σF(A) × B …… 其中F ∈ A

σF(A × B) == σF1(A) × σF2(B)

…… 其中F = F1 ∪ F2，F1∈A, F2 ∈B

σF(A × B) == σFX (σF1(A) × σF2(B))

…… 其中F = F1∪F2∪FX，F1∈A, F2 ∈B

Π p,q(A × B) == Π p(A) × Π q(B) …… 其中p∈A，q∈B

σF(A × B) == σF1(A) × σF2(B)

…… 其中F = F1 ∪ F2，F1∈A, F2 ∈B

σF(A × B) == σFx (σF1(A) × σF2(B))

…… 其中F = F1∪F2∪Fx，F1∈A, F2 ∈B

串接律

Π P=p1,p2,…pn(Π Q=q1,q2,…qn(A)) == Π P=p1,p2,…pn(A)……其中P ⊆ Q

σF1(σF2(A)) == σF1∧F2(A)

查询重写优化既可以基于关系代数的理论进行优化，例如谓词下推、子查询优化等，也可以基于启发式规则进行优化，例如Outer Join消除、表连接消除等。另外还有一些基于特定的优化规则和实际执行过程相关的优化，例如在并行扫描的基础上，可以考虑对Aggregation算子分阶段进行，通过将Aggregation划分成不同的阶段，可以提升执行的效率。
从另一个角度来看，查询重写是基于优化规则的等价变换，属于逻辑优化，也可以称为基于规则的优化，那么怎么衡量对一个SQL语句进行查询重写之后，它的性能一定是提升的呢？这时基于代价对查询重写进行评估就非常重要了，因此查询重写不只是基于经验的查询重写，还可以是基于代价的查询重写。
以谓词传递闭包和谓词下推为例，谓词的下推能够极大的降低上层算子的计算量，从而达到优化的效果，如果谓词条件有存在等值操作，那么还可以借助等值操作的特性来实现等价推理，从而获得新的选择条件。
例如，假设有两个表t1、t2分别包含[1,2,3,…100]共100行数据，那么查询语句SELECT t1.c1, t2.c1 FROM t1 JOIN t2 ON t1.c1=t2.c1 WHERE t1.c1=1则可以通过选择下推和等价推理进行优化，如图6-6所示。

图6-6 查询重写前后对比图

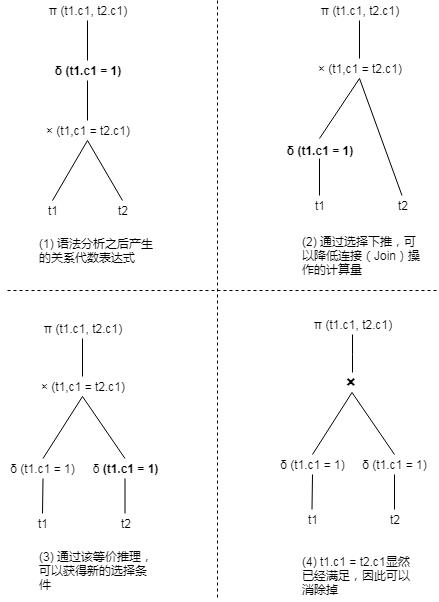
如图6-6-（1）所示，t1、t2表都需要全表扫描100行数据，然后再做join，生成100行数据的中间结果，最后再做选择操作，最终结果只有1行数据。如果利用等价推理，可以得到{t1.c1, t2.c1, 1}的是互相等价的，从而推导出新的t2.c1=1的选择条件，并把这个条件下推到t2上，从而得到图6-6-（4）重写之后的逻辑计划。可以看到，重写之后的逻辑计划，只需要从基表上面获取1条数据即可，join时内、外表的数据也只有1条，同时省去了在最终结果上的过滤条件，性能大幅提升。
在代码层面，查询重写的架构大致如图6-7所示。

图6-7 查询重写的架构

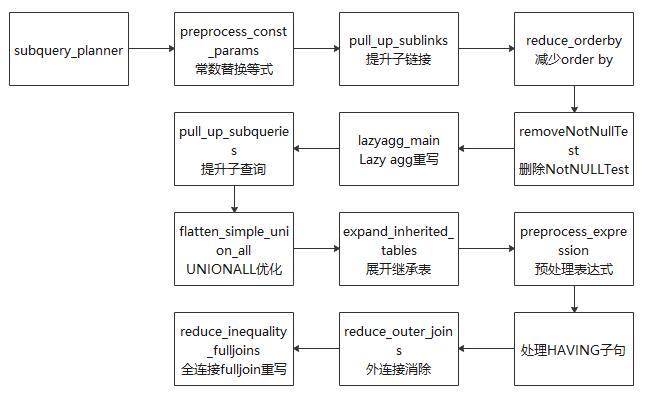
（1） 提升子查询：子查询出现在RangeTableEntry中，它存储的是一个子查询树，若子查询不被提升，则经过查询优化之后形成一个子执行计划，上层执行计划和子查询计划做嵌套循环得到最终结果。在该过程中，查询优化模块对这个子查询所能做的优化选择较少。若该子查询被提升，转换成与上层的join，由查询优化模块常数替换等式：由于常数引用速度更快，故将可以求值的变量求出来，并用求得的常数替换它，实现函数为preprocess_const_params。
（2） 子查询替换CTE：理论上CTE（common table expression，通用表达式）与子查询性能相同，但对子查询可以进行进一步的提升重写优化，故尝试用子查询替换CTE，实现函数为substitute_ctes_with_subqueries。
（3） multi count(distinct)替换为多条子查询：如果出现该类查询，则将多个count(distinct)查询分别替换为多条子查询，其中每条子查询中包含一个count(distinct)表达式，实现函数为convert_multi_count_distinct。
（4） 提升子链接：子链接出现在WHERE/ON等约束条件中，通常伴随着ANY/ALL/IN/EXISTS/SOME等谓词同时出现。虽然子链接从语句的逻辑层次上是清晰的，但是效率有高有低，比如相关子链接，其执行结果和父查询相关，即父查询的每一条元组都对应着子链接的重新求值，此情况下可通过提升子链接提高效率。在该部分数据库主要针对ANY和EXISTS两种类型的子链接尝试进行提升，提升为Semi Join或者Anti-SemiJoin，实现函数为pull_up_sublinks。
（5） 减少ORDER BY：由于在父查询中可能需要对数据库的记录进行重新排序，故减少子查询中的ORDER BY语句以进行链接可提高效率，实现函数为reduce_orderby。
（6） 删除NotNullTest：即删除相关的非NULL Test以提高效率，实现函数为removeNotNullTest。
（7） Lazy Agg重写：顾名思义，即“懒聚集”，目的在于减少聚集次数，实现函数为lazyagg_main。
（8） 对连接操作的优化做了很多工作，可能获得更好的执行计划，实现函数为pull_up_subqueries。
（9） UNION ALL优化：对顶层的UNION ALL进行处理，目的是将UNION ALL这种集合操作的形式转换为AppendRelInfo的形式，实现函数为flatten_simple_union_all。
（10） 展开继承表：如果在查询语句执行的过程中使用了继承表，那么继承表是以父表的形式存在的，需要将父表展开成为多个继承表，实现函数为expand_inherited_tables。，实现函数为expand_inherited_tables。
（11）预处理表达式：该模块是对查询树中的表达式进行规范整理的过程，包括对链接产生的别名Var进行替换、对常量表达式求值、对约束条件进行拉平、为子链接生成执行计划等，实现函数为preprocess_expression。
（12） 处理HAVING子句：在Having子句中，有些约束条件是可以转变为过滤条件的（对应WHERE），这里对Having子句中的约束条件进行拆分，以提高效率。
（13） 外连接消除：目的在于将外连接转换为内连接，以简化查询优化过程，实现函数为reduce_outer_join函数。
（14） 全连接full join重写：对全连接函数进行重写，以完善其功能。比如对于语句SELECT * FROM t1 FULL JOIN t2 ON TRUE可以将其转换为： SELECT * FROM t1 LEFT JOIN t2 ON TRUE UNION ALL (SELECT * FROM t1 RIGHT ANTI FULL JOIN t2 ON TRUE)，实现函数为reduce_inequality_fulljoins。
下面以子链接提升为例，介绍openGauss中一种最重要的子查询优化。所谓子链接（SubLink）是子查询的一种特殊情况，由于子链接出现在WHERE/ON等约束条件中，因此经常伴随ANY/EXISTS/ALL/IN/SOME等谓词出现，openGauss数据库为不同的谓词设置了不同的SUBLINK类型。代码如下：

Typedef enum SubLinkType {
    EXISTS_SUBLINK,
    ALL_SUBLINK,
    ANY_SUBLINK,
    ROWCOMPARE_SUBLINK,
    EXPR_SUBLINK,
    ARRAY_SUBLINK,
    CTE_SUBLINK
} SubLinkType;

openGauss数据库为子链接定义了单独的结构体——SubLink结构体，其中主要描述了子链接的类型、子链接的操作符等信息。代码如下：

Typedef struct SubLink {
    Expr xpr;
    SubLinkType subLinkType;
    Node* testexpr;
    List* operName;
    Node* subselect;
    Int location;
} SubLink;

子链接提升相关接口函数如图6-8所示。

图6-8 子链接相关接口函数

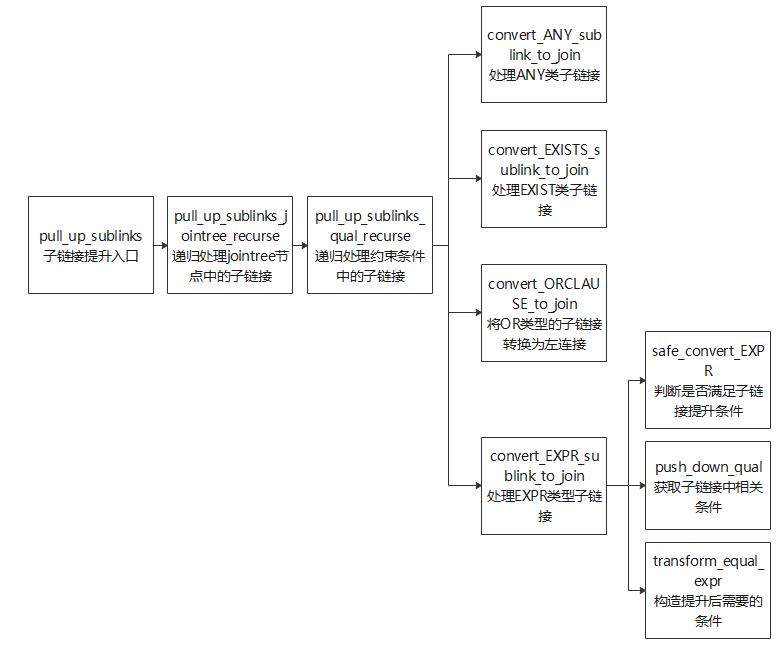
子链接提升的主要过程是在pull_up_sublinks函数中实现，pull_up_sublinks函数又调用pull_up_sublinks_jointree_recurse递归处理Query->jointree中的节点，函数输入参数如表6-8所示。

表6-8 函数输入参数说明

参数名

参数类型

说明

root

PlannerInfo*

输入参数，查询优化模块的上下文信息

jnode

Node*

输入参数，需要递归处理的节点，可能是RangeTblRef、FromExpr或JoinExpr

relids

Relids*

输出参数，jnode参数中涉及的表的集合

返回值

Node*

经过子链接提升处理之后的node节点

jnode分为三种类型：RangeTblRef、FromExpr、JoinExpr。针对这三种类型pull_up_sublinks_jointree_recurse函数分别进行了处理。

1）RangeTblRef
RangeTblRef是Query->jointree的叶子节点，所以是该函数递归结束的条件，程序走到该分支，一般有两种情况。
（1） 当前语句是单表查询而且不存在连接操作，这种情况递归处理直到结束后，再去查看子链接是否满足其他提升条件。
（2） 查询语句存在连接关系，在对From->fromlist、JoinExpr->larg或者JoinExpr->rarg递归处理的过程中，当遍历到了RangeTblRef叶子节点时，需要把RangeTblRef节点的relids（表的集合）返回给上一层。主要用于判断该子链接是否能提升。

2） FromExpr
（1） 递归遍历From->fromlist中的节点，之后对每个节点递归调用pull_up_sublinks_jointree_recurse函数，直到处理到叶子节点RangeTblRef才结束。
（2） 调用pull_up_sublinks_qual_recurse函数处理From->qual，对其中可能出现的ANY_SUBLINK或EXISTS_SUBLINK进行处理。

3） JoinExpr
（1） 调用pull_up_sublinks_jointree_recurse函数递归处理JoinExpr->larg和JoinExpr->rarg，直到处理到叶子节点RangeTblRef才结束。另外还需要根据连接操作的类型区分子链接是否能够被提升。
（2） 调用pull_up_sublinks_qual_recurse函数处理JoinExpr->quals，对其中可能出现的ANY_SUBLINK或EXISTS_SUBLINK做处理。如果连接类型不同，pull_up_sublinks_qual_recurse函数的available_rels1参数的输入值是不同的。
pull_up_sublinks_qual_recurse函数除了对ANY_SUBLINK和EXISTS_SUBLINK做处理，还对OR子句和EXPR类型子链接做了查询重写优化。其中Expr类型的子链接提升代码逻辑如下。
（1） 通过safe_convert_EXPR函数判断sublink是否可以提升。代码如下：

    //判断当前SQL语句是否满足sublink提升条件
    if (subQuery->cteList ||
        subQuery->hasWindowFuncs ||
        subQuery->hasModifyingCTE ||
        subQuery->havingQual ||
        subQuery->groupingSets ||
        subQuery->groupClause ||
        subQuery->limitOffset ||
        subQuery->rowMarks ||
        subQuery->distinctClause ||
        subQuery->windowClause) {
        ereport(DEBUG2,
            (errmodule(MOD_OPT_REWRITE),
                (errmsg("[Expr sublink pull up failure reason]: Subquery includes cte, windowFun, havingQual, group, "
                        "limitoffset, distinct or rowMark."))));
        return false;
}

（2） 通过push_down_qual函数提取子链接中相关条件。代码如下：

Static Node* push_down_qual(PlannerInfo* root, Node* all_quals, List* pullUpEqualExpr)
{
    If (all_quals== NULL) {
        Return NULL;
    }

    List* pullUpExprList = (List*)copyObject(pullUpEqualExpr);
    Node* all_quals_list = (Node*)copyObject(all_quals);

    set_varno_attno(root->parse, (Node*)pullUpExprList, true);
    set_varno_attno(root->parse, (Node*)all_quals_list, false);

    Relids varnos = pull_varnos((Node*)pullUpExprList, 1);
    push_qual_context qual_list;
    SubLink* any_sublink = NULL;
    Node* push_quals = NULL;
    Int attnum = 0;

    While ((attnum = bms_first_member(varnos)) >= 0) {
        RangeTblEntry* r_table = (RangeTblEntry*)rt_fetch(attnum, root->parse->rtable);

        //这张表必须是基表，否则不能处理
        If (r_table->rtekind == RTE_RELATION) {
        qual_list.varno = attnum;
        qual_list.qual_list = NIL;

        //获得包含特殊varno的条件
                get_varnode_qual(all_quals_list, &qual_list);

If (qual_list.qual_list != NIL && !contain_volatile_functions((Node*)qual_list.qual_list)) {
            any_sublink = build_any_sublink(root, qual_list.qual_list, attnum,pullUpExprList);
            push_quals = make_and_qual(push_quals, (Node*)any_sublink);
        }

        list_free_ext(qual_list.qual_list);
        }
   }

    list_free_deep(pullUpExprList);
    pfree_ext(all_quals_list);

    return push_quals;
}

（3） 通过transform_equal_expr函数构造需要提升的SubQuery（增加GROUP BY子句，删除相关条件）。代码如下：

    //为SubQuery增加GROUP BY和windowClasues
    if (isLimit) {
       append_target_and_windowClause(root,subQuery,(Node*)copyObject(node), false);
    } else {
        append_target_and_group(root, subQuery, (Node*)copyObject(node));
}
//删除相关条件
subQuery->jointree = (FromExpr*)replace_node_clause((Node*)subQuery->jointree,
         (Node*)pullUpEqualExpr,
         (Node*)constList,
         RNC_RECURSE_AGGREF | RNC_COPY_NON_LEAF_NODES);

（4） 构造需要提升的条件。代码如下：

//构造需要提升的条件
joinQual = make_and_qual((Node*)joinQual, (Node*)pullUpExpr);
…
Return joinQual;

（5） 生成join表达式。代码如下：

//生成join表达式
if (IsA(*currJoinLink, JoinExpr)) {
        ((JoinExpr*)*currJoinLink)->quals = replace_node_clause(((JoinExpr*)*currJoinLink)->quals, 
                                tmpExprQual, 
                                makeBoolConst(true, false),
                                RNC_RECURSE_AGGREF | RNC_COPY_NON_LEAF_NODES);
        
    } else if (IsA(*currJoinLink, FromExpr)) {
        ((FromExpr*)*currJoinLink)->quals = replace_node_clause(((FromExpr*)*currJoinLink)->quals, 
                                tmpExprQual, 
                                makeBoolConst(true, false),
                                RNC_RECURSE_AGGREF | RNC_COPY_NON_LEAF_NODES);
    }

    rtr = (RangeTblRef *) makeNode(RangeTblRef);
    rtr->rtindex = list_length(root->parse->rtable);
    
    // 构造左连接的JoinExpr
    JoinExpr *result = NULL;
    result = (JoinExpr *) makeNode(JoinExpr);
    result->jointype = JOIN_LEFT;
    result->quals = joinQual;
    result->larg = *currJoinLink;
    result->rarg = (Node *) rtr;

// 在rangetableentry中添加JoinExpr。在后续处理中，左外连接可转换为内连接
rte = addRangeTableEntryForJoin(NULL,
                                    NIL,
                                    result->jointype,
                                    NIL,
                                    result->alias,
                                    true);
    root->parse->rtable = lappend(root->parse->rtable, rte);

6.3.2 统计信息和代价估算

在不同数据分布下，相同查询计划的执行效率可能显著不同。因此，在选择计划时还应充分考虑数据分布对计划的影响。与通用逻辑优化不同，物理优化将计划的优化建立在数据之上，并通过最小化数据操作代价来提升性能。从功能上来看，openGauss的物理优化主要有以下3个关键步骤。
（1） 数据分布生成——从数据表中挖掘数据分布并存储。
（2） 计划代价评估——基于数据分布，建立代价模型评估计划的实际执行时间。
（3） 最优计划选择——基于代价估计，从候选计划中搜寻代价最小的计划。
首选，介绍数据分布的相关概念及其数据库内部的存储方式。

1. 数据分布的存储

数据集合D的分布由D上不同取值的频次构成。设D为表6-9在Grade列上的投影数据，该列有3个不同取值Grade = 1, 2, 3，其频次分布见表6-10。这里，将Grade取值的个数简称为NDV（Number of Distinct Values，不同值的数量）。

表6-9 Grade属性分布

Sno

Name

Gender

Grade

001

小张

男

1

002

小李

男

2

003

小王

男

3

004

小周

女

1

005

小陈

女

1

表6-10 Grade频次分布

Grade

1

2

3

频次

3

1

1

D D D可以涉及多个属性，将多个属性的分布称为联合分布。联合分布的取值空间可能十分庞大，从性能的角度考虑，数据库不会保存 D D D的联合分布，而是将 D D D中的属性分布分开保存，比如，数据库保存{ Gender=’男’}、{ Grade=’1’}的频次，而并不保存{ Gender=’男’, Grade=’1’}的频次。这种做法损失了 D D D上分布的很多信息。在随后的选择率与数据分布小节的内容将看到，在系统需要的时候，openGauss将采取预测技术对联合分布进行推测。虽然在某些情况下，这种推测的结果可能与实际出入较大。

数据分布的数据结构对于理解数据库如何存储该信息尤为关键。一般来说，KV（key-value）键值对是描述分布最常用的结构，其中key表示取值，value表示频次。但在NDV很大的情况下，key值的膨胀使得KV的存储与读取性能都不高。为提高效率，openGauss实际采用“KV向量+直方图”的混合方式表示属性分布。

数据分布的逻辑结构：高频值频次采用KV存储，存储结构被称为最常见值；除高频值以外的频次采用等高直方图（equal-bin-count histogram，EH）描述。实现中，openGauss会将频次最高的 k ( k = 100 ) k( k=100 ) k(k=100)个key值放入MCV，其余放入直方图表示。

值得注意的是，等高直方图会将多个值的频次合并存放，在显著提升存取效率的同时，也会使得分布模糊化。但在后续章节可以看到，相对于低频值，高频值对计划代价的估算更为关键。因此，采取这种以损失低频值准确性为代价，换取高性能的混合策略，无疑是一种相当划算的做法。

数据分布的存放位置：在openGauss中，MCV、直方图等信息实际是放在系统表PG_STATISTIC中的，表定义如表6-11所示。

表6-11 系统表PG\\_STATISTIC定义

starelid

staattnum

stanullfrac

stakind1

stanumbers1

stavalues1

Stakind2

……

0001

1

0

1

{0.2851, 0.1345}

{1, 2}

2

 

0001

2

0

1

{0.1955, 0.1741}

{数学, 语文}

2

 

表6-11中的一条元组存储了一条属性的统计信息。下分别对元组的属性意义进行解读。
（1） 属性starelid/staattnum表示的表OID和属性编号。
（2） 属性stanullfrac表示属性中为NULL的比例（为0表示该列没有NULL值）。
（3） 属性组{ stakind1, stanumbers1, stavalues1}构成PG_STATISTIC表的一个卡槽，存放表6-12中的一种数据结构类型的信息。在PG_STATISTIC表中有5个卡槽。一般情况下，第一个卡槽存储MCV信息，第二个卡槽存储直方图信息。以MCV卡槽为例：属性“stakind1”标识卡槽类型为MCV，其中“1”为“STATISTIC_KIND_MCV”的枚举值；属性stanumbers1与属性stavalues1记录MCV的具体内容，其中stavalues1记录key值，stanumbers1记录key对应的频次。上例中取值“1”的频次比例为0.2851，“2”的频次比例为0.1345。

表6-12 系统表PG\\_STATISTIC说明

类型

说明

STATISTIC_KIND_MCV

高频值（常见值），在一个列里出现最频繁的值，按照出现的频率进行排序，并且生成一个一一对应的频率数组，这样就能知道一个列中有哪些高频值，这些高频值的频率是多少

STATISTIC_KIND_HISTOGRAM

直方图，openGauss数据库用等频直方图来描述一个列中数据的分布，高频值不会出现在直方图中，这就保证了数据的分布是相对平坦的

STATISTIC_KIND_CORRELATION

相关系数，相关系数记录的是当前列未排序的数据分布和排序后的数据分布的相关性，这个值通常在索引扫描时用来估计代价，假设一个列未排序和排序之后的相关性是0，也就是完全不相关，那么索引扫描的代价就会高一些

STATISTIC_KIND_MCELEM

类型高频值（常见值），用于数组类型或者一些其他类型，openGauss数据库提供了ts_typanalyze系统函数来负责生成这种类型的统计信息

STATISTIC_KIND_DECHIST

数组类型直方图，用于给数组类型生成直方图，openGauss数据库提供了array_typanalyze系统函数来负责生成这种类型的统计信息

注意，数据分布和PG_STATISTIC表中的内容不是在创建表的时候自动生成的，其生成的触发条件是用户对表进行了analyze操作。

2. 数据分布抽取方法

数据分布的存储给出了数据分布在openGauss的逻辑结构和存储方式。那么上面介绍的数据分布信息是如何从数据中获得呢？针对该问题，下面将简要介绍openGauss抽取分布的主要过程。为加深对方法的理解，先分析该问题面临的挑战。
获取分布最直接的办法是遍历所有数据，并通过计数直接生成MCV和直方图信息。但现实中的数据可能是海量的，遍历的I/O代价往往不可接受。比如，银行的账单数据涉及上千亿条记录，需要TB级的存储。除I/O代价外，计数过程的内存消耗也可能超过上限，这也使得算法实现变得尤为困难。因此，更现实的做法是降低数据分析的规模，采用小样本分析估算整体数据分布。那么，样本选择的好坏就显得尤为重要。
目前，openGauss数据库的样本生成过程在acquire_sample_rows函数实现，它采用了两阶段采样的算法对数据分布进行估算。第一阶段使用S算法对物理页进行随机采样，生成样本S1；第二阶段使用Z（Vitter）算法对S1包含的元组进行蓄水池采样，最终生成一个包含3000元组的样本S2。两阶段算法可以保证S2是原数据的一个无偏样本。因此，可以通过分析S2推断原数据分布，并将分布信息记录在PG_STATISTIC表的对应元组中。
openGauss将样本的生成划分成两个步骤，主要是为了提高采样效率。该方法的理论依据依赖于以下现实条件：数据所占据的物理页数量M可以准确获得，而每个物理页包含的元组数n未知。由于M已知，S算法可以用1/M的概率对页进行均匀抽样，可以生成原数据的小样本S1。一般认为，某元组属于任一物理页是等概率事件，这就保证了S1是一个无偏样本；而由于S1包含的元组远少于原数据，在S1的基础上进行二次抽样代价将大大减少。第二阶段没有继续使用S算法的主要原因是：S1的元组总数N未知（因为n未知），该算法无法获得采样概率——1/N。而Z（Vitter）的算法是一种蓄水池抽样算法，这类算法可以在数据总量未知条件下保证采样的均匀。蓄水池抽样算法原理不是本书的重点，读者可以自行查阅资料。

3. 选择率与数据分布

SQL查询常常带有where约束（过滤条件），比如：Select * from student where gender = ‘male’； Select * from student where grade > ‘1’。那么，约束对于查询结果的实际影响是什么呢？为度量约束的效能，首先引入选择率的概念。

选择率：给定查询数据集 C C C（ C C C可为数据表或任何中间结果集合）和约束表达式 x x x， x x x相对 C C C的选择率定义为

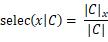
其中，表示 ∣ C ∣ |C| ∣C∣的总记录数，表示 ∣ C x ∣ |C_x| ∣Cx​∣上满足x约束的记录数。如表6-13所示，在 x x x为“grade = 1”时， s e l e c ( x ∣ C ) selec(x|C) selec(x∣C)=3/5。

表6-13 数据集C选择率结果

Sno

Name

Gender

Grade

001

小张

男

1

002

小李

男

2

003

小王

男

3

004

小周

女

1

005

小陈

女

1

记 C C C的数据分布为 π π π。从定义可知， s e l e c ( x ∣ C ) selec(x|C) selec(x∣C)其实是对 π π π按照语义 x x x的一种描述。从这里可看到数据分布的关键用处：数据分布可以辅助选择率的计算、而使得计算过程不必遍历原数据。在代价估算部分中，将看到选择率对计划代价估算的巨大作用。
根据该思路，介绍openGauss计算选择率的基本过程。注意，由于简单约束下的选择率计算具有代表性，本部分将主要围绕着该进行问题进行讲解。简单约束的定义为：仅涉及基表单个属性的非范围约束。
涉及非简单约束选择率的计算方法，读者可以参照本章自行阅读源码。

1） 简单约束的选择率计算

假设 x x x为简单约束，且 x x x所涉及的属性分布信息已存在于PG_STATISTIC表元组 r r r中（参见数据分布的存储部分内容）。openGauss通过调用clause_selectivity函数将元组 r r r按 x x x要求转换为选择率。
clause_selectivity的第二个参数clause为约束语句 x x x。面对不同SQL查询，输入clause_selectivity的clause可能有多种类型，典型类型如表6-14所示。

表6-14 简单约束类型

简单约束类型

实例

Var

SELECT * FROM PRODUCT WHERE ISSOLD;

Const

SELECT * FROM PRODUCT WHERE TRUE;

Param

SELECT * FROM PRODUCT WHERE $1;

OpExpr

SELECT * FROM PRODUCT WHERE PRIZE = ‘100’;

AND

SELECT * FROM PRODUCT WHERE PRIZE = ‘100’ AND TYPE = ‘HAT’;

OR

SELECT * FROM PRODUCT WHERE PRIZE = ‘100’ OR TYPE = ‘HAT’;

NOT

SELECT * FROM PRODUCT WHERE NOT EXIST TYPE = ‘HAT’;

其他

 

{Var, Const, Param, OpExpr}属于基础约束类型，而包含{AND, OR, NOT}的约束都是建立约束基础上的集合运算，称为SET约束类型。进一步观察可以发现，约束{Var, Const, Param}可以看作OpExpr约束的一个特例。比如：“SELECT * FROM PRODUCT WHERE ISSOLD”与“SELECT * FROM PRODUCT WHERE ISSOLD = TRUE”等价。限于篇幅，这里将着重介绍基于OpExpr类型的选择率计算，并简要给出SET类型计算的关键逻辑。
（1） OpExpr类型选择率。
以查询语句SELECT * FROM PRODUCT WHERE PRIZE = ‘100’为例。clause_selectivity函数首先根据clause（PRIZE = ‘100’）类型找到OpExpr分支。然后调用treat_as_join_clause函数判断clause是否是一个join约束；结果为假，说明clause是过滤条件（OP），则调用restriction_selectivity函数对clause参数进行选择率估算。代码如下：

Selectivity
clause_selectivity(PlannerInfo *root,
    Node *clause,
    int varRelid,
    JoinType jointype,
    SpecialJoinInfo *sjinfo)
{
  Selectivity s1 = 0.5;/* default for any unhandled clause type */
  RestrictInfo *rinfo = NULL;

  if (clause == NULL)      /* can this still happen? */
    return s1;
  if (IsA(clause, Var))...
  else if (IsA(clause, Const))...
  else if (IsA(clause, Param))
  
// not子句处理分支
else if (not_clause(clause))
  {
    /* inverse of the selectivity of the underlying clause */
    s1 = 1.0 - clause_selectivity(root,
                                   (Node *) get_notclausearg((Expr *) clause),
                                   varRelid,
                                   jointype,
                                   sjinfo);
}
  
// and子句处理分支
else if (and_clause(clause))
  {
    /* share code with clauselist_selectivity() */
    s1 = clauselist_selectivity(root,
                                   ((BoolExpr *) clause)->args,
                                   varRelid,
                                   jointype,
                                   sjinfo);
  }
  
  // or子句处理分支
else if (or_clause(clause))
  {
    ListCell   *arg;

    s1 = 0.0;
    foreach(arg, ((BoolExpr *) clause)->args)
    {
        Selectivity s2 = clause_selectivity(root,
                                    (Node *) lfirst(arg),
                                   varRelid,
                                   jointype,
                                   sjinfo);

      s1 = s1 + s2 - s1 * s2;
    }
  }
   
   // join或op子句处理分支
 else if (is_opclause(clause) || IsA(clause, DistinctExpr))
  {
    OpExpr   *opclause = (OpExpr *) clause;
    Oidopno = opclause->opno;

    // join子句处理
if (treat_as_join_clause(clause, rinfo, varRelid, sjinfo))
    {
      /* Estimate selectivity for a join clause. */
      s1 = join_selectivity(root, opno,
                                             opclause->args,
                                             opclause->inputcollid,
                                             jointype,
                                             sjinfo);
    }
    
   // op子句处理
else
    {
      /* Estimate selectivity for a restriction clause. */
      s1 = restriction_selectivity(root, opno,
                                             opclause->args,
                                             opclause->inputcollid,
                                             varRelid);
    }
  }
  ... ...
  return s1;
}

restriction_selectivity函数识别出PRIZE = ‘100’是形如Var = Const的等值约束，它将通过eqsel函数间接调用var_eq_const函数进行选择率估算。在该过程中，var_eq_const函数会读取PG_STATISTIC表中PRIZE列分布信息，并尝试利用信息中MCV计算选择率。首选调用get_attstatsslot函数判断‘100’是否存在于MCV中，有以下几种情况。

情况1：存在，直接从MCV中返回‘100’的占比作为选择率。
情况2：不存在，则计算高频值的总比例sumcommon，并返回(1.0 – sumcommon – nullfrac) / otherdistinct作为选择率。其中，nullfrac是NULL的比例，otherdistinct是低频值的NDV。

加入查询的约束是PRIZE < ‘100’，restriction_selectivity函数，该约束将根据操作符类型调用scalargtsel函数并尝试利用PG_STATISTIC表中信息计算选择率。由于满足< ‘100’的值可能分别存在于MCV和直方图中，所以需要分别在两种结构中收集满足条件的值。相比于MCV来说，在直方图中收集满足条件值的过程较为复杂，因此下面重点介绍：借助于直方图key的有序性，openGauss采用二分查找快速搜寻满足条件的值，并对其总占比进行求和并记作selec_histogram。注意，等高直方图不会单独记录‘100’的频次，而是将‘100’和相邻值合并放入桶(记作B桶)中，并仅记录B中数值的总频次(Fb)。为解决该问题，openGauss假设桶中元素频次相等，并采用公式 B 中 小 于 100 值 的 个 数 B 所 有 取 值 个 数 ∗ F b \\frac{B中小于100值的个数}{B所有取值个数} \\ast{F_b} B所有取值个数B中小于100值的个数​∗openGauss数据库源码解析系列文章——存储引擎源码解析

openGauss数据库源码解析系列文章——公共组件源码解析（上）

openGauss数据库源码解析系列文章——存储引擎源码解析

openGauss数据库源码解析系列文章——数据安全技术（上）

openGauss数据库源码解析系列文章—— 事务机制源码解析

⭐openGauss数据库源码解析系列文章—— 对象权限管理⭐