生存分析——泊松回归(LightGBM)实现生存分析

Posted 2021-09-05 悟乙己

You can find the full article here

来看一个比较特殊的Survival分析建模的案例,利用的是半参模型:Poisson Regression
具体参考文章:Survival Analysis with LightGBM plus Poisson Regression
里面的建模思路非常有意思，不适合工业落地，不过咨询公司的data scientist看过来~

---

1 Poisson Regression

1.1 松泊分布与泊松回归

参考：什么是松泊分布？泊松回归可以用来做什么？

试想一下，你现在就站在一个人流密集的马路旁，打算收集闯红灯的人群情况（？）。
首先，利用秒表和计数器，一分钟过去了，有5个人闯红灯；
第二分钟有4个人；而下一分钟有4个人。
持续记录下去，你就可以得到一个模型，这便是“泊松分布”的原型。

除此以外，现实生活中还有很多情况是服从泊松分布的：

• 10分钟内从ATM中取钱的人数
• 一天中发生车祸的次数
• 每100万人中患癌症的人数
• 单位面积土地内昆虫的数目

Poisson模型(泊松回归模型)是用于描述单位时间、单位面积或者单位容积内某事件发现的频数分布情况，
通常用于描述稀有事件（即小概率）事件发生数的分布。

上述例子中都明显的一个特点：
低概率性，以及单位时间(或面积、体积)内的数量。
通常情况下，满足以下三个条件时，可认为数据满足Poisson分布：

• (1) 平稳性：发生频数的大小，只与单位大小有关系（比如1万为单位，或者100万为单位时患癌症人数不同）；
• (2) 独立性：发生频数的大小，各个数之间没有影响关系，即频数数值彼此独立没有关联关系；
  比如前1小时闯红灯的人多了，第2小时闯红灯人数并不会受影响；
• (3) 普通性：发生频数足够小，即低概率性。

如果数据符合这类特征时，而又想研究X对于Y的影响（Y呈现出Poisson分布）；
此时则需要使用Poisson回归，而不是使用常规的线性回归等。

1.2 LightGBM 实现泊松回归的案例

参考来源：https://github.com/Microsoft/LightGBM/issues/807

import lightgbm as lgb
import numpy as np
import pandas as pd

n=100000
lam = .01
X = np.floor(np.random.lognormal(size=(n,2))).astype(int)
y = np.maximum(X[:,0],X[:,1])+np.random.poisson(lam=lam, size=n)

train_inds = np.arange(int(n/3))
val_inds =   np.arange(int(n/3), int(2*n/3))
test_inds =   np.arange(int(2*n/3), int(n))

X_test, y_test = X[test_inds,:], y[test_inds]

ds = lgb.Dataset(X,y, categorical_feature=[1])

ds_train = ds.subset(train_inds)
ds_val = ds.subset(val_inds)

params = {'objective':'poisson',
         'metric':'rmse',
         'learning_rate':.1
         }
gbm = lgb.train(params, ds_train, num_boost_round=300, early_stopping_rounds=20, valid_sets=[ds_val, ds_train], 
                verbose_eval=100, categorical_feature=[1])

yhat = gbm.predict(X_test)
print('neg obs:', len(yhat[yhat<0]))

y是需要服从poisson分布的

2 数据解读

2.1 数据样式

数据集解释：美国Washington, D.C.的一个共享单车公司
数据来源：bike-sharing-dataset
数据集的中文字段解释：
参考：Capital Bikeshare （美国Washington, D.C.的一个共享单车公司）提供的自行车数据上进行回归分析
具体实现 + 代码：Survival_LGBM-github

# 字段说明Instant 记录号

Dteday：日期
Season：季节
    1=春天
    2=夏天
    3=秋天
    4=冬天
yr：年份，(0: 2011, 1:2012)
mnth：月份( 1 to 12)
hr：小时 (0 to 23) （只在 hour.csv 有，作业忽略此字段）
holiday：是否是节假日
weekday：星期中的哪天，取值为 0～6
workingday：是否工作日
    1=工作日 （非周末和节假日）
    0=周末
weathersit：天气
1：晴天，多云
2：雾天，阴天
3：小雪，小雨
4：大雨，大雪，大雾
temp：气温摄氏度
atemp：体感温度
hum：湿度
windspeed：风速

y值
-   casual：非注册用户个数
-  registered：注册用户个数
-  cnt：给定日期（天）时间（每小时）总租车人数，响应变量 y

现在数据变成：

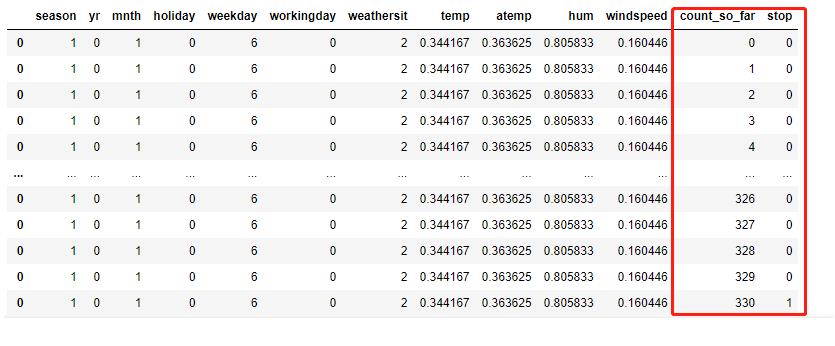
也就是把第一行数据，拆分成330行，新增了两列：

• count_so_far就是人员计数从[0,1,2,3,4,6,…,330]，
• stop，就是人数终止计数

这样构造的一个特殊的数据结构，造就了该模型object的独特，原文自评:

We solve a not classical survival problem where we have not to estimate the probability of surviving past time, but we estimate the probability that a specific event occurs at the end of the day. This is a simple example but it shows how to applicate survival modeling techniques, with classical instruments, in a not common scenario where our duty is to estimate a probability density function.

这里就把问题变成了，2011/1/1 这天，
在casual users = 0的时候，不会停止增长；在casual users = 1，不会停止增长；…；在casual users = 330，停止增长
最后，如何来预测临时用户的人数？
用的是一个“可能在什么数量上停止”的曲线，这里是把 hazard = 临时用户的增长量，会拟合一个达到预测数值的可能性趋势。

这里跟生存分析 以及常规回归的差异：

• 常规回归模型，y~x1+x2… 根据特征直接预测临时用户人数，点估计；这里的Poisson有点类似加强版区间估计，就叫趋势估计？
• 生存分析，
  • 生存函数使用的是KM曲线，计算不同生存时间区间下的存活率；
  • 风险函数，计算不同生存时间区间下的风险值

2.2 衡量模型指标

2.2.1 CRPS

我们对结果的评价是用这种任务的标准分数来进行的。连续排序概率评分(Continuous ranking Probability Score, CRPS)将MAE推广到概率预测的情况。

在涉及概率预测的情况下，CPRS是应用最广泛的精度指标之一。它需要对所涉及的整个概率函数进行评估，因此需要对每个每日样本的整个生存曲线进行估计。

PDF / CDF

• 概率密度函数probability density function（pdf）

• 累积分布函数(Cumulative Distribution Function)，又叫分布函数
  

2.2 训练与解读

数据的延展：

### EXPAND TRAIN DATA ###

X_train['count_so_far'] = X_train.apply(lambda x: np.arange(x.casual), axis=1)
X_train['stop'] = X_train.apply(lambda x: np.append(np.zeros(x.casual-1), 1), axis=1)
X_train = X_train.apply(pd.Series.explode)   # 数据扩充的方式

X_train['count_so_far'] = X_train.count_so_far.astype(int)
X_train['stop'] = X_train.stop.astype(int)

y_train = X_train['stop']
X_train = X_train[columns+['count_so_far']]

print(X_train.shape)
X_train

### EXPAND VALID DATA FOR PREDICTION ###

X_val_surv = df[(df.dteday >= datetime(year=2012, month=1, day=1))&(df.dteday < datetime(year=2012, month=5, day=1))].copy()

X_val_surv['count_so_far'] = X_val_surv.apply(lambda x: np.arange(max_count), axis=1)
X_val_surv['stop'] = X_val_surv.apply(lambda x:np.append(np.zeros(x.casual), np.ones(max_count-x.casual)), axis=1)
X_val_surv = X_val_surv.apply(pd.Series.explode)

X_val_surv['count_so_far'] = X_val_surv.count_so_far.astype(int)
X_val_surv['stop'] = X_val_surv.stop.astype(int)

y_val_surv = X_val_surv['stop']
X_val_surv = X_val_surv[columns+['count_so_far']]

print(X_val_surv.shape)

具体的已经在2.1 描述过了；这里要额外来看一下max_count，这个在train数据集中不会出现，
也就是今天有多少临时用户，就是多少X_train.apply(lambda x: np.arange(x.casual), axis=1)
但你会看到，X_val_surv是X_val_surv.apply(lambda x: np.arange(max_count), axis=1)，这里就是临时用户的最大值设定为4000，这个值根据临时用户max值来取的，就是临时用户上线。

params = {
         'objective':'poisson',
         'num_leaves':30, 
         'learning_rate': 0.001,
         'feature_fraction': 0.8,
         'bagging_fraction': 0.9,
         'bagging_seed': 33,
         'poisson_max_delta_step': 0.8,
         'metric': 'poisson'
         }

### FIT LGBM WITH POISSON LOSS ### 

trn_data = lgb.Dataset(X_train, label=y_train)
val_data = lgb.Dataset(X_val, label=y_val)

model = lgb.train(params, trn_data, num_boost_round=1000,
                  valid_sets = [trn_data, val_data],
                  verbose_eval=50, early_stopping_rounds=150)

这里X_train的shape为：(247252, 13)，那么可以知道训练集是非常大的；
需要重置数据，可到：

### PREDICT HAZARD FUNCTION ON VALIDATION DATA AND TRANSFORM TO SURVIVAL ###

p_val_hz = model.predict(X_val_surv).reshape(-1,max_count)
p_val = 1-np.exp(-np.cumsum(p_val_hz, axis=1))
X_val_surv.shape
>>> (484000, 12)
p_val.shape
>>> (121, 4000)

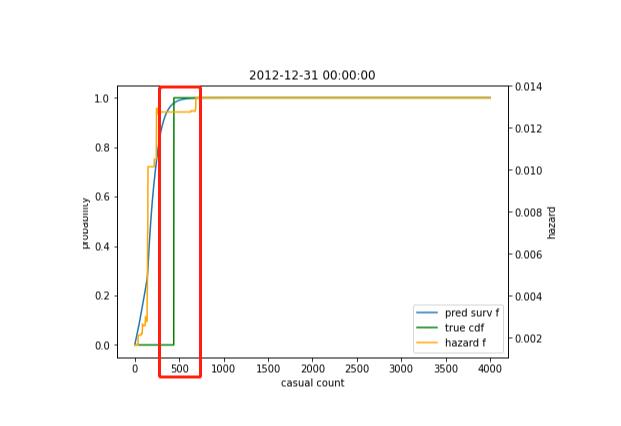
p_val就回归正常，代表着每一天，不同人群数量的概率，直接上图：

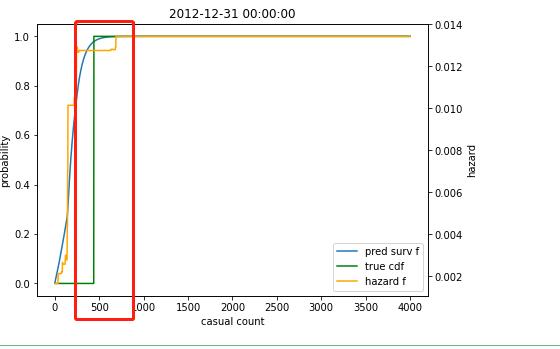
这天在500左右，达到峰值了，那么这天临时用户的预测值就在500左右了。

简单的模型检验：

### CRPS ON VALIDATION DATA ###
crps(t_val, p_val)
>>> 0.17425293919055515
### CRPS ON VALIDATION DATA WITH BASELINE MODEL ###
crps(t_val, np.repeat(cdf, len(t_val)).reshape(-1,max_count))

---

3 同等lightGBM分类测试

https://blog.csdn.net/wang263334857/article/details/81836578

来看一下同一份数据测试出来的结果如何，后续不贴太多，只贴一下我测试的代码，放在了之前的一个项目下面：Survival_Poisson_Regression