LeetCode 516. 最长回文子序列(区间dp) / 36. 有效的数独/73. 矩阵置零/496. 下一个更大元素 I / 456. 132 模式(特别的单调栈)
Posted Zephyr丶J
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了LeetCode 516. 最长回文子序列(区间dp) / 36. 有效的数独/73. 矩阵置零/496. 下一个更大元素 I / 456. 132 模式(特别的单调栈)相关的知识,希望对你有一定的参考价值。
516. 最长回文子序列
2021.8.12 每日一题
题目描述
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
示例 1:
输入:s = “bbbab”
输出:4
解释:一个可能的最长回文子序列为 “bbbb” 。
示例 2:
输入:s = “cbbd”
输出:2
解释:一个可能的最长回文子序列为 “bb” 。
提示:
1 <= s.length <= 1000
s 仅由小写英文字母组成
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/longest-palindromic-subsequence
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
经典区间dp问题,注意遍历顺序就可以
class Solution {
public int longestPalindromeSubseq(String s) {
int l = s.length();
int[][] dp = new int[l][l];
for(int i = 0; i < l; i++){
dp[i][i] = 1;
}
int max =1;
for(int i = l - 2; i >= 0; i--){
for(int j = i + 1; j < l; j++){
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
if(s.charAt(i) == s.charAt(j)){
dp[i][j] = Math.max(dp[i][j], dp[i + 1][j - 1] + 2);
}
max = Math.max(max, dp[i][j]);
}
}
return max;
}
}
区间dp,三叶姐给出的普遍思路:
1.从小到大枚举区间长度len
2.枚举左边下标l,根据区间长度计算出又端点r
3.求dp[l][r]
把这个模版也记住!!!
class Solution {
public int longestPalindromeSubseq(String s) {
int n = s.length();
char[] cs = s.toCharArray();
int[][] f = new int[n][n];
for (int len = 1; len <= n; len++) {
for (int l = 0; l + len - 1 < n; l++) {
int r = l + len - 1;
if (len == 1) {
f[l][r] = 1;
} else if (len == 2) {
f[l][r] = cs[l] == cs[r] ? 2 : 1;
} else {
f[l][r] = Math.max(f[l + 1][r], f[l][r - 1]);
f[l][r] = Math.max(f[l][r], f[l + 1][r - 1] + (cs[l] == cs[r] ? 2 : 0));
}
}
}
return f[0][n - 1];
}
}
作者:AC_OIer
链接:https://leetcode-cn.com/problems/longest-palindromic-subsequence/solution/gong-shui-san-xie-qu-jian-dp-qiu-jie-zui-h2ya/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
评论区大佬思路,将字符串翻转,然后求两个字符串的最长公共子序列:
class Solution {
public int longestPalindromeSubseq(String s) {
int l = s.length();
//翻转字符串
String r = new StringBuffer(s).reverse().toString();
//两个字符串的最长公共子序列
int[][] dp = new int[l + 1][l + 1];
for(int i = 1; i <= l; i++){
for(int j = 1; j <= l; j++){
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
if(s.charAt(i - 1) == r.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1] + 1;
}
}
}
return dp[l][l];
}
}
36. 有效的数独
题目描述
请你判断一个 9x9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 ‘.’ 表示。
注意:
一个有效的数独(部分已被填充)不一定是可解的。
只需要根据以上规则,验证已经填入的数字是否有效即可。
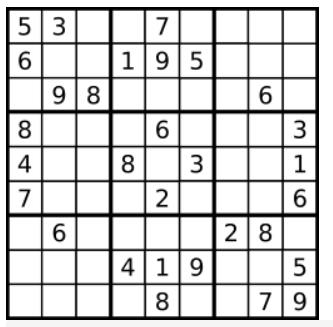
示例 1:
输入:board =
[[“5”,“3”,".",".",“7”,".",".",".","."]
,[“6”,".",".",“1”,“9”,“5”,".",".","."]
,[".",“9”,“8”,".",".",".",".",“6”,"."]
,[“8”,".",".",".",“6”,".",".",".",“3”]
,[“4”,".",".",“8”,".",“3”,".",".",“1”]
,[“7”,".",".",".",“2”,".",".",".",“6”]
,[".",“6”,".",".",".",".",“2”,“8”,"."]
,[".",".",".",“4”,“1”,“9”,".",".",“5”]
,[".",".",".",".",“8”,".",".",“7”,“9”]]
输出:true
示例 2:
输入:board =
[[“8”,“3”,".",".",“7”,".",".",".","."]
,[“6”,".",".",“1”,“9”,“5”,".",".","."]
,[".",“9”,“8”,".",".",".",".",“6”,"."]
,[“8”,".",".",".",“6”,".",".",".",“3”]
,[“4”,".",".",“8”,".",“3”,".",".",“1”]
,[“7”,".",".",".",“2”,".",".",".",“6”]
,[".",“6”,".",".",".",".",“2”,“8”,"."]
,[".",".",".",“4”,“1”,“9”,".",".",“5”]
,[".",".",".",".",“8”,".",".",“7”,“9”]]
输出:false
解释:除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
提示:
board.length == 9
board[i].length == 9
board[i][j] 是一位数字或者 ‘.’
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/valid-sudoku
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
class Solution {
public boolean isValidSudoku(char[][] board) {
//用哈希表记录每一行,每一列,每一个宫内出现的数字
//如果相同的就返回fasle
//9行,9列,9个宫
int l = board.length;
boolean[][] row = new boolean[l][10];
boolean[][] col = new boolean[l][10];
boolean[][] mat = new boolean[l][10];
for(int i = 0; i < l; i++){
for(int j = 0; j < l; j++){
if(board[i][j] == '.')
continue;
int t = board[i][j] - '0';
int idx = i / 3 * 3 + j / 3;
if(row[i][t] || col[j][t] || mat[idx][t])
return false;
row[i][t] = true;
col[j][t] = true;
mat[idx][t] = true;
}
}
return true;
}
}
73. 矩阵置零
题目描述
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
进阶:
一个直观的解决方案是使用 O(mn) 的额外空间,但这并不是一个好的解决方案。
一个简单的改进方案是使用 O(m + n) 的额外空间,但这仍然不是最好的解决方案。
你能想出一个仅使用常量空间的解决方案吗?
示例 1:
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-2^31 <= matrix[i][j] <= 2^31 - 1
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/set-matrix-zeroes
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
空间复杂度m+n的方法:
class Solution {
public void setZeroes(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
boolean[] row = new boolean[m];
boolean[] col = new boolean[n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == 0) {
row[i] = col[j] = true;
}
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (row[i] || col[j]) {
matrix[i][j] = 0;
}
}
}
}
}
主要是空间复杂度O1的方法难想
class Solution {
public void setZeroes(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
//要用O1的空间,很自然会想到用特殊的数去标记需要置0的位置,但是矩阵中的数取了整型所有值,所以不行
//然后想和m+n的解法一样,用一行一列去标记
//很自然会想到用第一行和第一列
//那么第一行和第一列本身用什么标记呢,就是两个变量
//那么一个变量可以吗,当然可以
//用一个变量去标记第一列是否需要置0
//然后用第一列标记每一行是否需要置0,第一行去标记这一列
//用第一行标记每一列是否需要置0
boolean flag = false;
for(int i = 0; i < m; i++){
//第一列
if(matrix[i][0] == 0)
flag = true;
for(int j = 1; j < n; j++){
if(matrix[i][j] == 0)
matrix[i][0] = matrix[0][j] = 0;
}
}
//这里考虑一下怎么修改这个状态
//因为要用到第一行和第一列,所以需要先把别的行列修改了,再修改第一行和第一列
//所以从下至上
for(int i = m - 1; i >= 0; i--){
for(int j = 1; j < n; j++){
if(matrix[i][0] == 0 || matrix[0][j] == 0)
matrix[i][j] = 0;
}
//遍历完这一行,可以更改第一列的状态了
if(flag)
matrix[i][0] = 0;
}
}
}
496. 下一个更大元素 I
题目描述
给你两个 没有重复元素 的数组 nums1 和 nums2 ,其中nums1 是 nums2 的子集。
请你找出 nums1 中每个元素在 nums2 中的下一个比其大的值。
nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在,对应位置输出 -1 。
示例 1:
输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
对于 num1 中的数字 4 ,你无法在第二个数组中找到下一个更大的数字,因此输出 -1 。
对于 num1 中的数字 1 ,第二个数组中数字1右边的下一个较大数字是 3 。
对于 num1 中的数字 2 ,第二个数组中没有下一个更大的数字,因此输出 -1 。
示例 2:
输入: nums1 = [2,4], nums2 = [1,2,3,4].
输出: [3,-1]
解释:
对于 num1 中的数字 2 ,第二个数组中的下一个较大数字是 3 。
对于 num1 中的数字 4 ,第二个数组中没有下一个更大的数字,因此输出 -1 。
提示:
1 <= nums1.length <= nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 10^4
nums1和nums2中所有整数 互不相同
nums1 中的所有整数同样出现在 nums2 中
进阶:你可以设计一个时间复杂度为 O(nums1.length + nums2.length) 的解决方案吗?
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/next-greater-element-i
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
这道题咋说呢,如果要实现最后复杂度的要求
应该算个中等题,单调栈思路
class Solution {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
//记得上次是不会做的,尽管是简单题
//思路:要在O1内找到比当前大的
//首先处理nums2,用栈处理,单调栈,找第一个比自己大的,存入map中
int l = nums2.length;
Stack<Integer> stack = new Stack<>();
Map<Integer, Integer> map = new HashMap<>();
stack.push(nums2[0]);
for(int i = 1; i < l; i++){
int temp = nums2[i];
while(!stack.isEmpty() && temp > stack.peek()){
int p = stack.pop();
map.put(p, temp);
}
stack.push(temp);
}
while(!stack.isEmpty()){
map.put(stack.pop(), -1);
}
int[] res = new int[nums1.length];
for(int i = 0; i < nums1.length; i++){
int temp = nums1[i];
res[i] = map.get(temp);
}
return res;
}
}
456. 132 模式
题目描述
给你一个整数数组 nums ,数组中共有 n 个整数。132 模式的子序列 由三个整数 nums[i]、nums[j] 和 nums[k] 组成,并同时满足:i < j < k 和 nums[i] < nums[k] < nums[j] 。
如果 nums 中存在 132 模式的子序列 ,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [1,2,3,4]
输出:false
解释:序列中不存在 132 模式的子序列。
示例 2:
输入:nums = [3,1,4,2]
输出:true
解释:序列中有 1 个 132 模式的子序列: [1, 4, 2] 。
示例 3:
输入:nums = [-1,3,2,0]
输出:true
解释:序列中有 3 个 132 模式的的子序列:[-1, 3, 2]、[-1, 3, 0] 和 [-1, 2, 0] 。
提示:
n == nums.length
1 <= n <= 2 * 10^5
-10^9 <= nums[i] <= 10^9
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/132-pattern
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
这道题我竟然还做过
先很自信的写了一个这样的代码
class Solution {
public boolean find132pattern(int[] nums) {
//单调栈
//如果比当前栈顶元素小,就弹出,然后记录这个最小元素min
//如果比栈顶元素大,就放入,然后遇到一个在min和栈顶之间的,就满足条件
Stack<Integer> stack = new Stack<>();
int l = nums.length;
stack.push(nums[0]);
int min = nums[0];
for(int i = 1; i < l; i++){
int temp = nums[i];
if(temp > min && temp < stack.peek())
return true;
while(!stack.isEmpty() && stack.peek() >=以上是关于LeetCode 516. 最长回文子序列(区间dp) / 36. 有效的数独/73. 矩阵置零/496. 下一个更大元素 I / 456. 132 模式(特别的单调栈)的主要内容,如果未能解决你的问题,请参考以下文章