AtCoder Regular Contest 124(练习)

Posted 2021-09-05 佐鼬Jun

A - LR Constraints

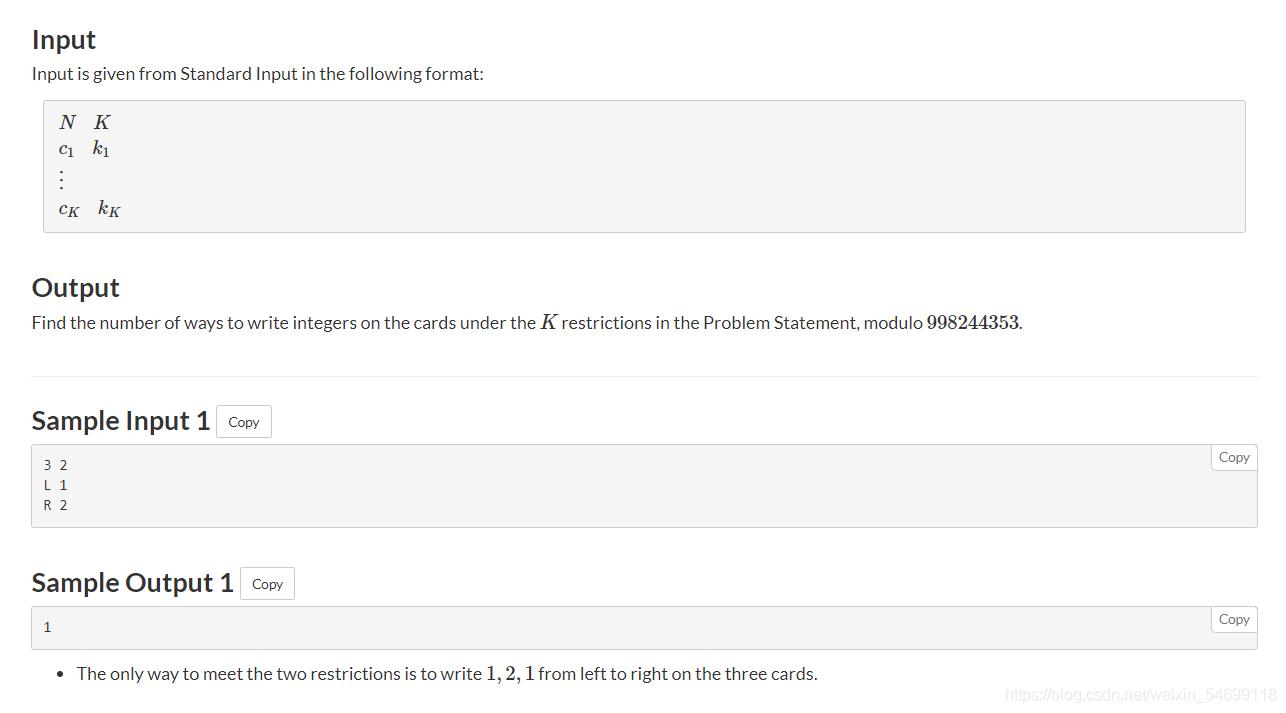
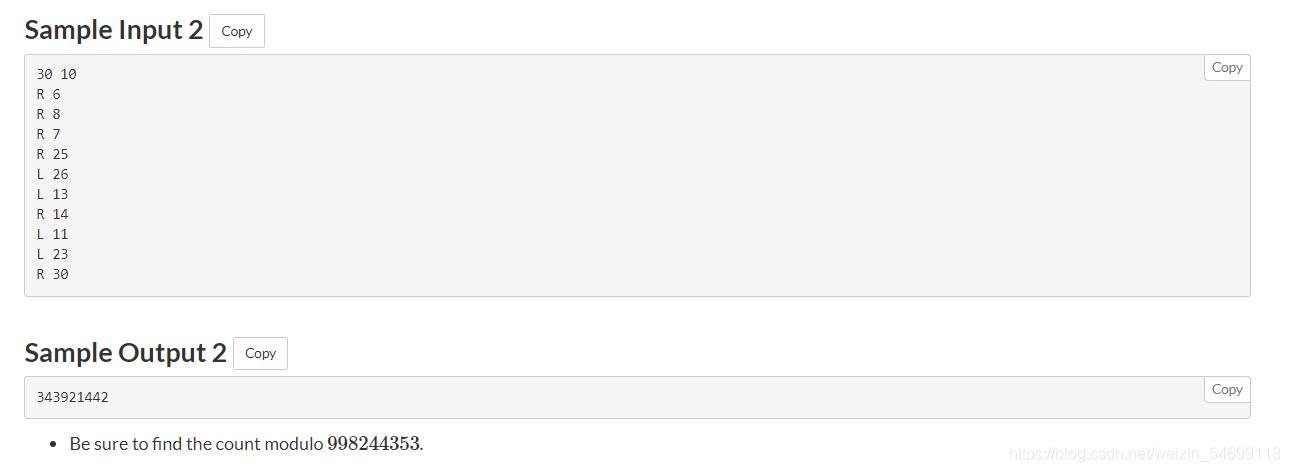
题意： N张卡片，每个卡片上的数字不超过K，且有K种限制，若$c_i$是‘L’,则$ki$这个位置必须是数字$k_i$,且从左往右数这个位置必须是第一次出现$k_i$这个数字的位置，若$c_i$是‘R’,则$ki$这个位置必须是数字$k_i$,且从左往右数这个位置必须是最后一个出现$k_i$这个数字的位置，现在问你在这些限制下，有多少种卡牌摆放方案
思路： 没有限制的情况下，每个位置都可以放k种卡片，有了限制后，对于指定位置，只能放要求的卡片，其他位置可以随便放，若出现‘L’则该位置左边就不能出现$c_i$这个数字，相当于$K-1$，‘R’就是该位置右边不能出现这个数字，也相当于$K-1$,所以开个桶记录每个位置可能出现的数字数量就行

#include <bits/stdc++.h>
using namespace std;
const int N = 111111;
const long long mod = 998244353;
#define ll long long
ll res = 1;
int M[N];
int main() {
    int n, k;
    cin >> n >> k;
    for (int i = 1; i <= n; i++) {
        M[i] = k;
    }
    for (int j = 0; j < k; j++) {
        char op;
        int x;
        cin >> op >> x;
        M[x] = 1;
        if (op == 'L') {
            for (int i = 1; i <= x - 1; i++) {
                M[i] = max(1, M[i] - 1);
            }
        } else {
            for (int i = x + 1; i <= n; i++) {
                M[i] = max(1, M[i] - 1);
            }
        }
    }
    for (int i = 1; i <= n; i++) {
        res = (ll)res * M[i] % mod;
    }
    printf("%lld\\n", res % mod);
    return 0;
}

B - XOR Matching 2

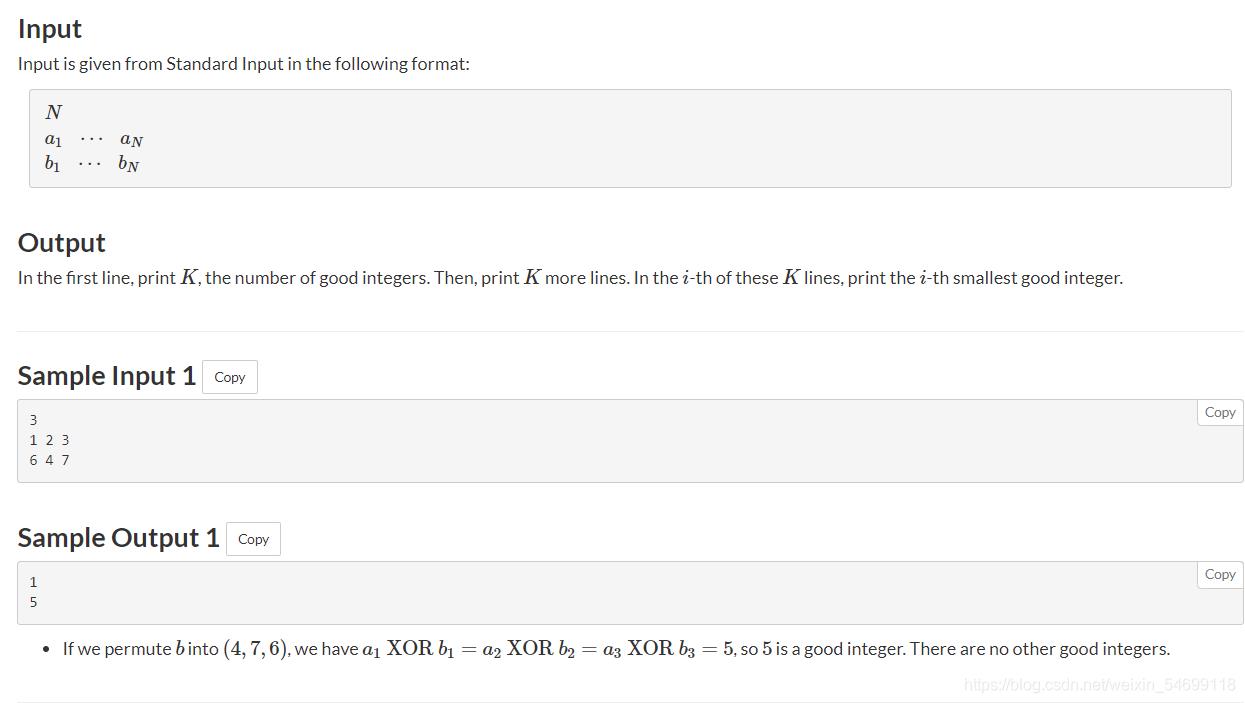
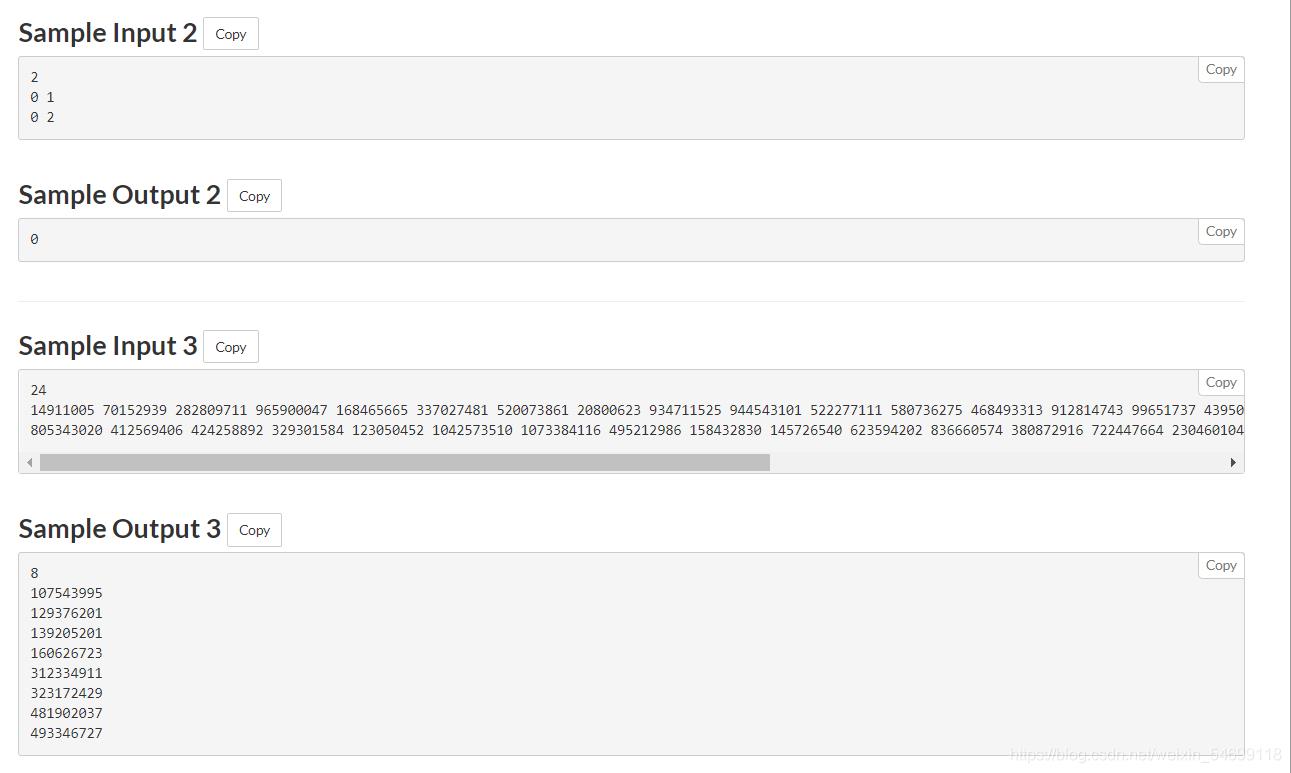
题意： 给定长度为n的两个数组a和b，问你能否重新排列b数组，使得$a_1$^$b_1$ $a_2$^$b_2$… $a_n$^$b_n$,如果能的话，输出不同异或值的数量，且把所有的异或值输出
思路：
可以枚举每个$b_i$与$a_1$进行异或，用异或的值再分别与每个$a_i$进行异或运算，把得出来的值排个序，与b数组进行比较，如果一样，说明这是一种方案，因为异或的逆运算还是异或，所以再异或一次后，如果是满足题意的，那么一定会异或出原来的值，开个vector来记录每种可行方案的异或值，最后记得去重即可，异或值一样的算重复

#include <bits/stdc++.h>
using namespace std;
const int N = 2222;
#define ll long long
ll a[N], b[N];

vector<ll> res;
int main() {
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%lld", &a[i]);
    }
    for (int i = 0; i < n; i++) {
        scanf("%lld", &b[i]);
    }

    vector<ll> c;
    sort(a, a + n);
    sort(b, b + n);

    for (int i = 0; i < n; i++) {
        ll x = a[0] ^ b[i];
        c.clear();
        for (int j = 0; j < n; j++) {
            ll y = x ^ a[j];
            c.push_back(y);
        }
        sort(c.begin(), c.end());
        int flag = 1;
        for (int j = 0; j < n; j++) {
            if (b[j] != c[j]) {
                flag = 0;
                break;
            }
        }
        if (flag) res.push_back(x);
    }

    sort(res.begin(), res.end());
    res.erase(unique(res.begin(), res.end()), res.end());

    printf("%d\\n", res.size());
    
    for (int i = 0; i < res.size(); i++) {
        printf("%d\\n", res[i]);
    }
    return 0;
}

C - LCM of GCDs

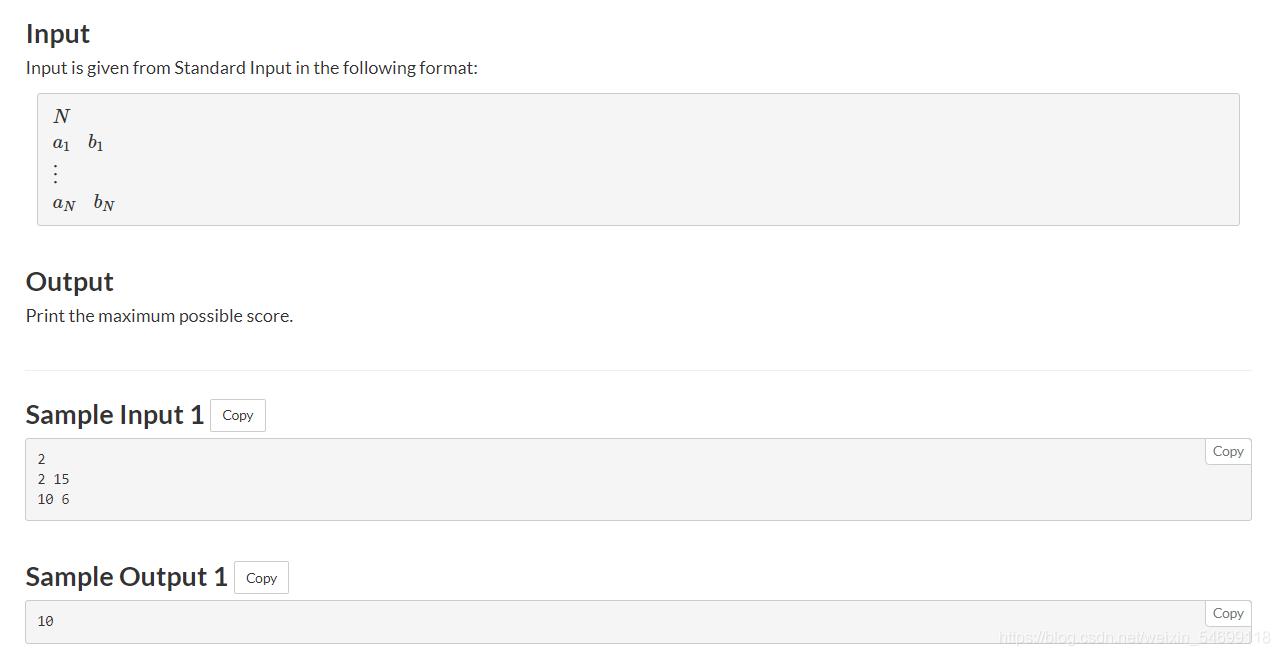
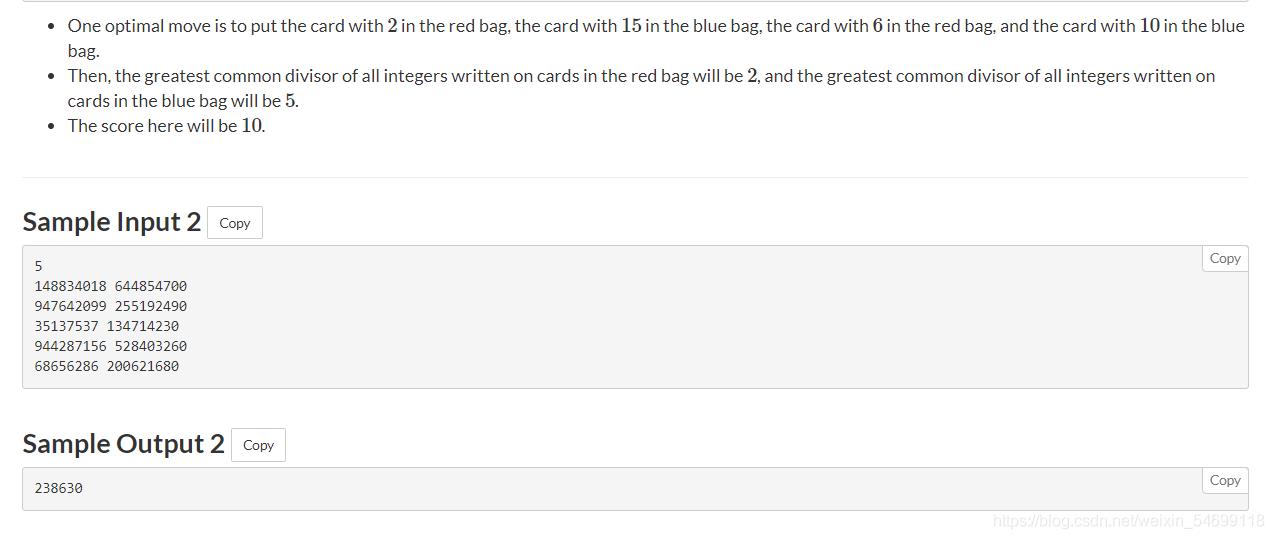
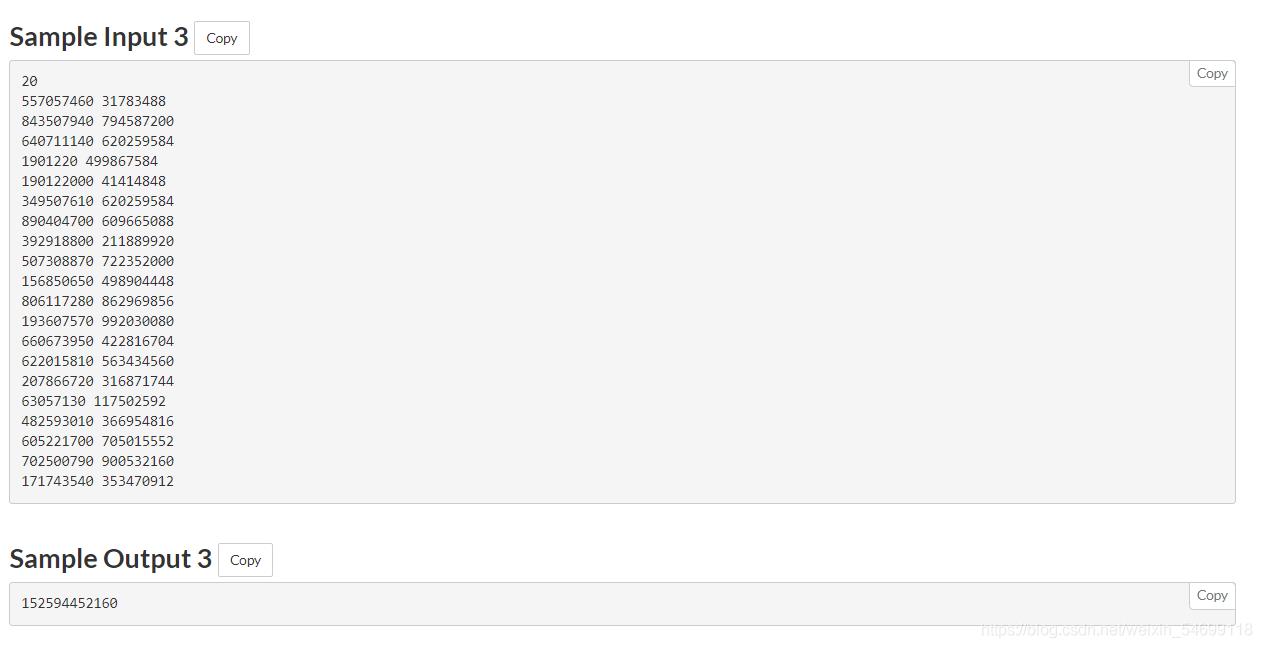
题意： 有n个卡包，每个卡包里面有2张卡片，每个卡片有相应的点数，每张卡片都可以选择放在红袋子里，或者蓝袋子，一张卡片放在红，那另一张就要放在蓝，题目要求让你求出红袋子所有卡片点数的最大公约数，和蓝袋子里所有卡片点数的最大公约数(gcd)，然后用两个最大公约数求出两数的最小公倍数(lcm)。
思路：
先对两个数（a1和b1就行，因为a1和b1肯定要分在不同的组，他们俩的约数之一，一定就是整个袋子的约数）进行求所有约数(除数)
然后枚举约数，假设A组有x个约数，B组月y个约数，那么一共就有$x\cdot y$种约数组合，枚举所有的约数组合，只要
所有的数都能整除这个约数，就说明它可以作为他们组的最大公约数出现，此时求出合法方案的约数组合，对于每个合法的约数组合求出它们的最小公倍数即可，然后取最大的就行。
也可以dfs爆搜+记忆化
知识点： 1.两个数大，不代表两数的最小公倍数就大
2.int范围内，一个数最多有$2^9$个因子

#include <bits/stdc++.h>
using namespace std;
#define ll long long
int n;
int a[55], b[55];

vector<int> divide(int x) {
    vector<int> res;
    for (int i = 1; i <= x / i; i++) {
        if (x % i == 0) {
            res.push_back(i);
            if (x / i != i) res.push_back(x / i);
        }
    }
    return res;
}
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d%d", &a[i], &b[i]);
    }
    ll res;
    ll ans = 0;
    vector<int> A, B;
    A = divide(a[1]);
    B = divide(b[1]);
    for (auto x : A) {
        for (auto y : B) {
            int flag = 1;
            for (int i = 1; i <= n; i++) {
                if (a[i] % x == 0 && b[i] % y == 0) continue;
                if (b[i] % x == 0 && a[i] % y == 0) continue;
                flag = 0;
                break;
            }
            if (flag) {
                int t = __gcd(x, y);
                res = (ll)x * y / t;
                ans = max(ans, res);
            }
        }
    }
    cout << ans << endl;
}

D - Yet Another Sorting Problem

这是一位大佬写的题解，比较好懂，过于愚钝一时间没理解，直接放大佬代码
链接: link.

To be continued
如果你有任何建议或者批评和补充，请留言指出，不胜感激