Connectivity(并查集)

Posted 2021-09-05 佐鼬Jun

D - Connectivity

-abc049




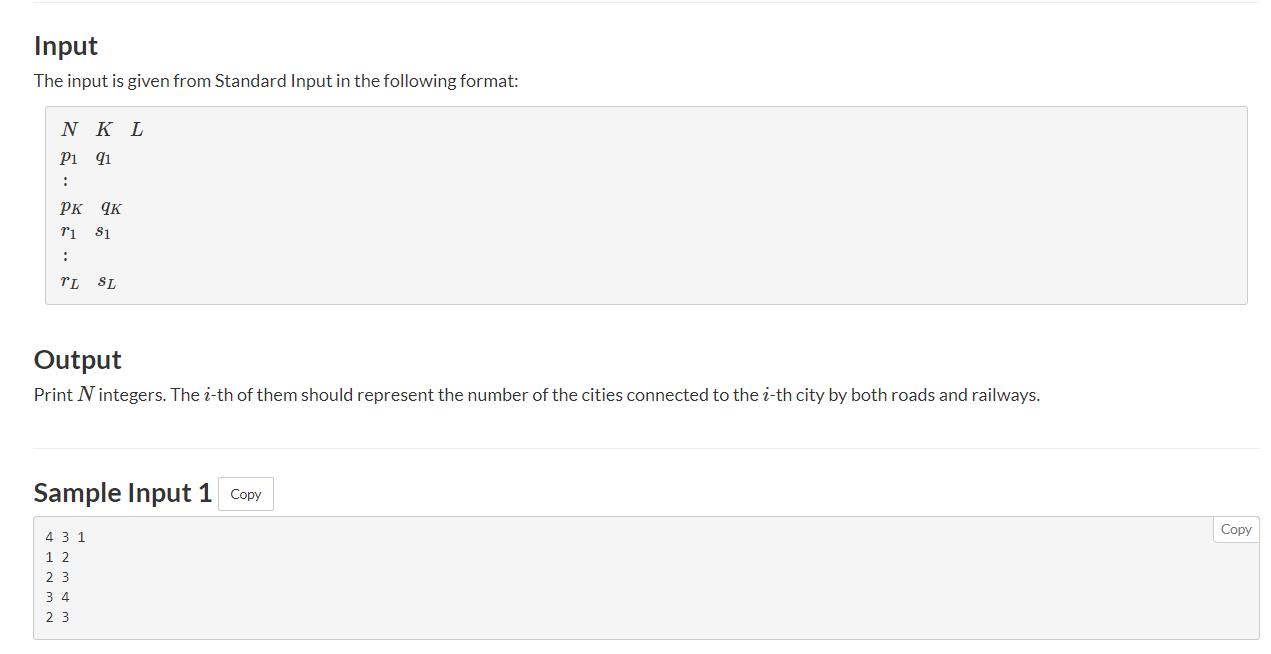
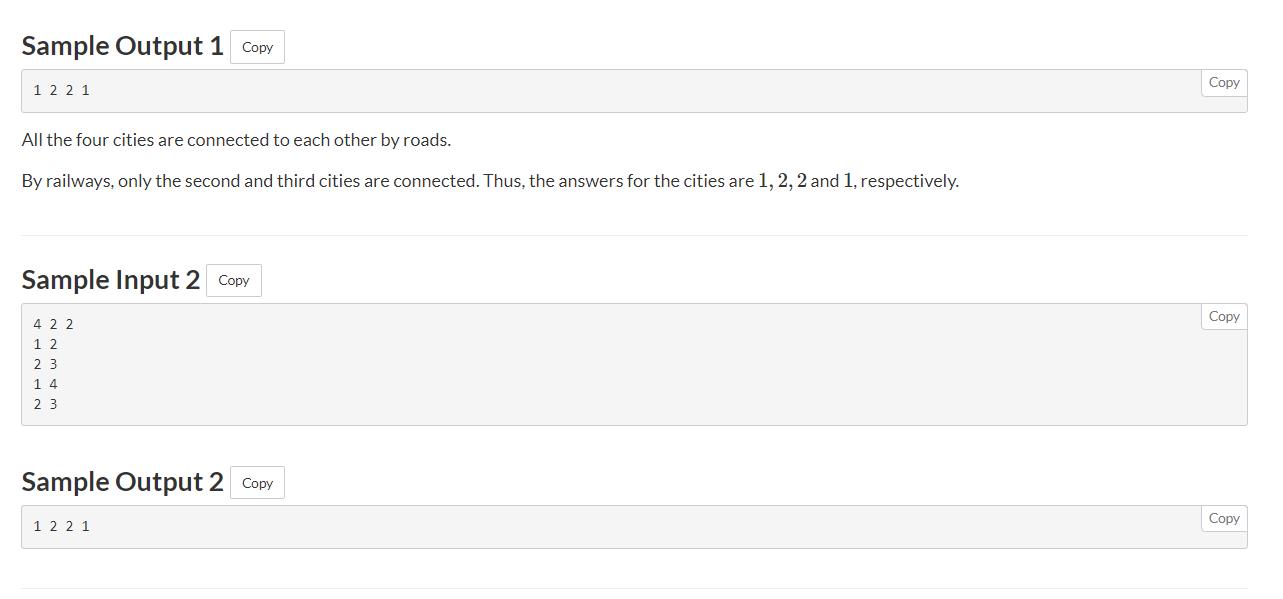
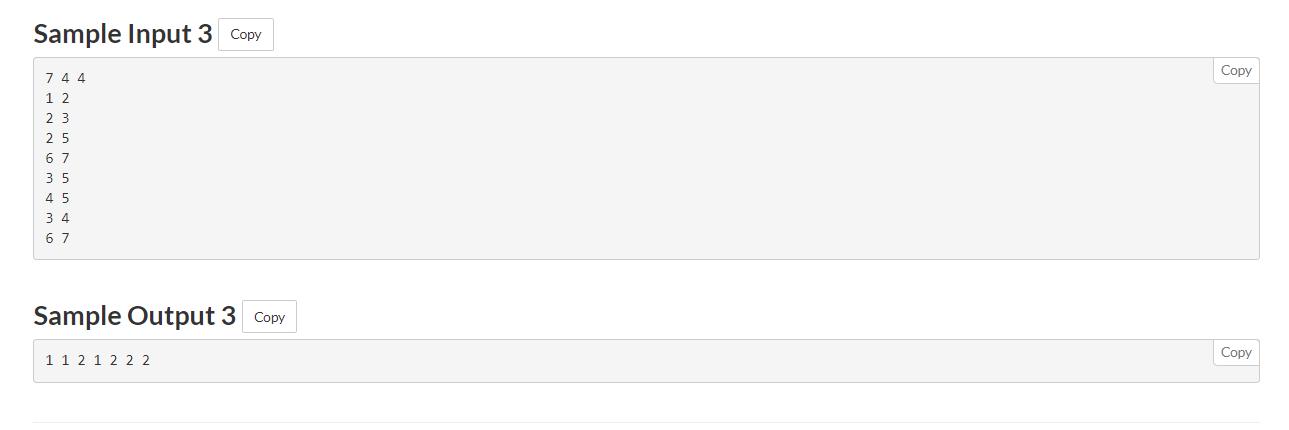
题意： 有n个点，k条公路，$l$条铁路，公路和铁路都是连接两个点的边，没有重边，只要A和B点能通过公路相通，就说明A和B使公路连接，铁路连接和这个一样，现在问，对于每个点来说，有多少个点是通过铁路和公路与这个点相连通(自己算连接自己)
(题意读了半天没读懂，样例都没研究出来 )
思路： 其实题目简化问题就是通过公路与当前点相连的点与通过铁路与当前点相连的点的交集。开两种并查集，来记录哪些点是通过公路和铁路与当前点相连，然后开个Map来存交集个数，Map里面存的就是父亲节点对的个数，对于集合里的元素来说，对于每个点通过找集合的祖先结点来计数，明显是可以的。
注意：并查集记录完后，要先完全路径压缩一遍，否则会出现父亲节点不是祖先结点的问题。

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
typedef pair<int, int> PII;
int fa1[N], fa2[N];
int n, k, l;
int find(int x, int *fa) {
    if (x != fa[x]) fa[x] = find(fa[x], fa);
    return fa[x];
}
void Union(int x, int y, int *fa) {
    int fx = find(fa[x], fa), fy = find(fa[y], fa);
    if (fx != fy) {
        fa[fx] = fy;
    }
}
int main() {
    scanf("%d%d%d", &n, &k, &l);
    for (int i = 0; i < N; i++) {
        fa1[i] = i, fa2[i] = i;
    }
    while (k--) {
        int a, b;
        scanf("%d%d", &a, &b);
        Union(a, b, fa1);
    }
    while (l--) {
        int a, b;
        scanf("%d%d", &a, &b);
        Union(a, b, fa2);
    }
    for (int i = 1; i <= n; i++) {
        find(i, fa1), find(i, fa2);
    }
    map<PII, int> m;
    for (int i = 1; i <= n; i++) {
        m[{fa1[i], fa2[i]}]++;
    }
    for (int i = 1; i <= n; i++) {
        printf("%d ", m[{fa1[i], fa2[i]}]);
    }
    puts("");
    return 0;
}

To be continued
如果你有任何建议或者批评和补充，请留言指出，不胜感激