LeetCode 22. 括号生成c++/java详细题解

Posted 2021-09-05 林深时不见鹿

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了LeetCode 22. 括号生成c++/java详细题解相关的知识，希望对你有一定的参考价值。

1、题目

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

输入：n = 1
输出：["()"]

提示：

1 <= n <= 8

2、思路

(dfs) $O(C_{2n}^{n})$

首先我们需要知道一个结论，一个合法的括号序列需要满足两个条件：

1、左右括号数量相等
2、任意前缀中左括号数量 >= 右括号数量（也就是说每一个右括号总能找到相匹配的左括号）

题目要求我们生成n对的合法括号序列组合，可以考虑使用深度优先搜索，将搜索顺序定义为枚举序列的每一位填什么，那么最终的答案一定是有n个左括号和n个右括号组成。

如何设计dfs搜索函数？

最关键的问题在于搜索序列的当前位时，是选择填写左括号，还是选择填写右括号？因为我们已经知道一个合法的括号序列，任意前缀中左括号数量一定 >= 右括号数量，因此，如果左括号数量不大于 n，我们就可以放一个左括号，来等待一个右括号来匹配。如果右括号数量小于左括号的数量，我们就可以放一个右括号，来使一个右括号和一个左括号相匹配。

递归搜索树如下：

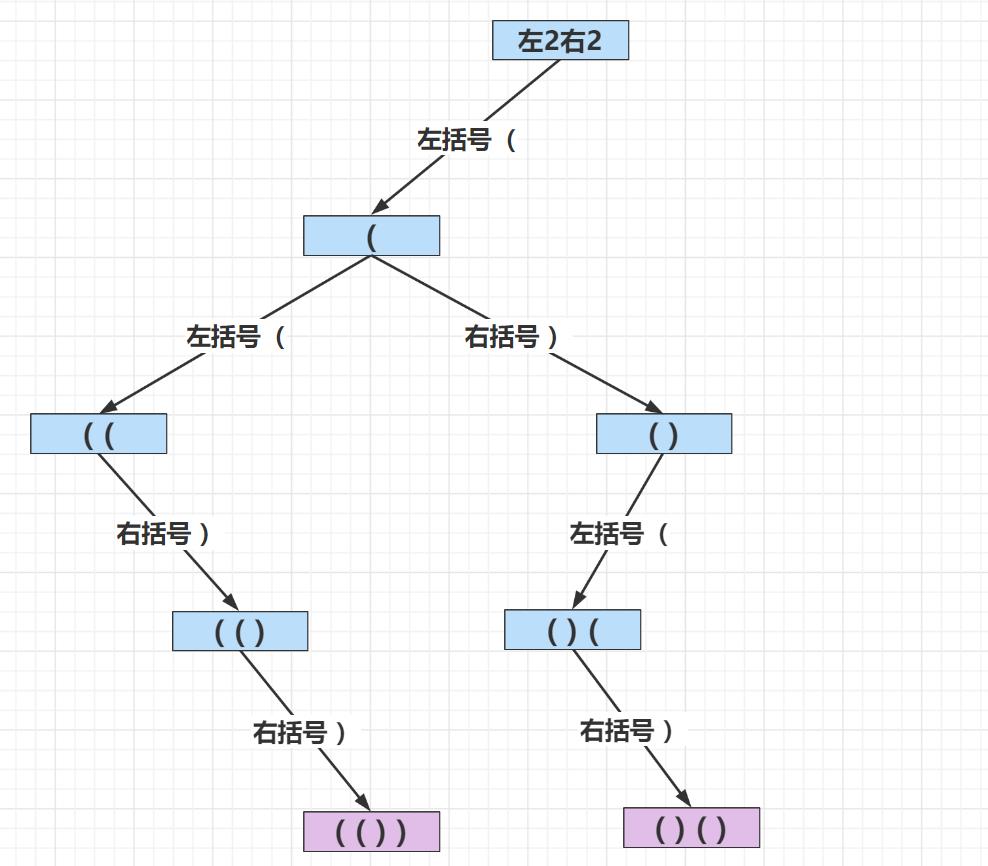
递归函数设计

void dfs(int n ,int lc, int rc ,string str)

n是括号对数，lc是左括号数量，rc是右括号数量，str是当前维护的合法括号序列。

搜索过程如下：

1、初始时定义序列的左括号数量lc 和右括号数量rc都为0。
2、如果 lc < n，左括号的个数小于n，则在当前序列str后拼接左括号。
3、如果 rc < n && lc > rc , 右括号的个数小于左括号的个数，则在当前序列str后拼接右括号。
4、当lc == n && rc == n 时，将当前合法序列str加入答案数组res中。

时间复杂度分析： 经典的卡特兰数问题，因此时间复杂度为 $O(\\frac{1}{n+1}C_{2n}^{n}) = O(C_{2n}^n)$ 。

3、c++代码

class Solution {
public:
    vector<string> res; //记录答案 
    vector<string> generateParenthesis(int n) {
        dfs(n , 0 , 0, "");
        return res;
    }
    void dfs(int n ,int lc, int rc ,string str)
    {
        if( lc == n && rc == n) res.push_back(str);   
        else
        {
            if(lc < n) dfs(n, lc + 1, rc, str + "(");
            if(rc < n && lc > rc) dfs(n, lc, rc + 1, str + ")");
        }
    }
};

4、java代码

class Solution {
    static List<String> res = new ArrayList<String>();  //记录答案 

    public List<String> generateParenthesis(int n) {
        res.clear();
        dfs(n, 0, 0, "");
        return res;
    }
    public void dfs(int n ,int lc, int rc ,String str)
    {
        if( lc == n && rc == n) res.add(str);   
        else
        {
            if(lc < n) dfs(n, lc + 1, rc, str + "(");
            if(rc < n && lc > rc) dfs(n, lc, rc + 1, str + ")");
        }
    }
}