LeetCode 130. 被围绕的区域

Posted 2021-09-05 ZSYL

LeetCode 130. 被围绕的区域

• 题目描述
• DFS
• • Java
  • Python
• BFS
• • Java
  • Python

题目描述

给你一个 m x n 的矩阵 board ，由若干字符 ‘X’ 和 ‘O’ ，找到所有被 ‘X’ 围绕的区域，并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。

示例：

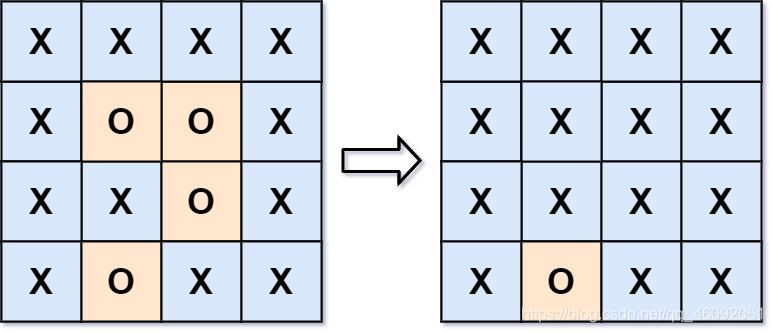
输入：board = [[“X”,“X”,“X”,“X”],[“X”,“O”,“O”,“X”],[“X”,“X”,“O”,“X”],[“X”,“O”,“X”,“X”]]
输出：[[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“O”,“X”,“X”]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 ‘O’ 都不会被填充为 ‘X’。 任何不在边界上，或不与边界上的 ‘O’ 相连的 ‘O’ 最终都会被填充为 ‘X’。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

DFS

写在前面

本题给定的矩阵中有三种元素：

• 字母 X；
• 被字母 X 包围的字母 O；
• 没有被字母 X 包围的字母 O。

本题要求将所有被字母 X 包围的字母 O都变为字母 X ，但很难判断哪些 O 是被包围的，哪些 O 不是被包围的。

注意到题目解释中提到：任何边界上的 O 都不会被填充为 X。 我们可以想到，所有的不被包围的 O 都直接或间接与边界上的 O 相连。我们可以利用这个性质判断 O 是否在边界上，具体地说：

• 对于每一个边界上的 O，我们以它为起点，标记所有与它直接或间接相连的字母 O；
• 最后我们遍历这个矩阵，对于每一个字母：
  • 如果该字母被标记过，则该字母为没有被字母 X 包围的字母 O，我们将其还原为字母 O；
  • 如果该字母没有被标记过，则该字母为被字母 X 包围的字母 O，我们将其修改为字母 X。

深度优先搜索

思路及解法

我们可以使用深度优先搜索实现标记操作。在下面的代码中，我们把标记过的字母 O 修改为字母 A。

Java

class Solution {
    int n, m;

    public void solve(char[][] board) {
        n = board.length;
        if (n == 0) {
            return;
        }
        m = board[0].length;
        for (int i = 0; i < n; i++) {
            dfs(board, i, 0);
            dfs(board, i, m - 1);
        }
        for (int i = 1; i < m - 1; i++) {
            dfs(board, 0, i);
            dfs(board, n - 1, i);
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (board[i][j] == 'A') {
                    board[i][j] = 'O';
                } else if (board[i][j] == 'O') {
                    board[i][j] = 'X';
                }
            }
        }
    }

    public void dfs(char[][] board, int x, int y) {
        if (x < 0 || x >= n || y < 0 || y >= m || board[x][y] != 'O') {
            return;
        }
        board[x][y] = 'A';
        dfs(board, x + 1, y);
        dfs(board, x - 1, y);
        dfs(board, x, y + 1);
        dfs(board, x, y - 1);
    }
}

Python

class Solution:
    def solve(self, board: List[List[str]]) -> None:
        if not board:
            return
        
        n, m = len(board), len(board[0])

        def dfs(x, y):
            if not 0 <= x < n or not 0 <= y < m or board[x][y] != 'O':
                return
            
            board[x][y] = "A"
            dfs(x + 1, y)
            dfs(x - 1, y)
            dfs(x, y + 1)
            dfs(x, y - 1)
        
        for i in range(n):
            dfs(i, 0)
            dfs(i, m - 1)
        
        for i in range(m - 1):
            dfs(0, i)
            dfs(n - 1, i)
        
        for i in range(n):
            for j in range(m):
                if board[i][j] == "A":
                    board[i][j] = "O"
                elif board[i][j] == "O":
                    board[i][j] = "X"

复杂度分析

• 时间复杂度：O(n×m)，其中 n 和 m 分别为矩阵的行数和列数。深度优先搜索过程中，每一个点至多只会被标记一次。
• 空间复杂度：O(n×m)，其中 n 和 m 分别为矩阵的行数和列数。主要为深度优先搜索的栈的开销。

BFS

思路及解法

我们可以使用广度优先搜索实现标记操作。在下面的代码中，我们把标记过的字母 O 修改为字母 A。

Java

class Solution {
    int[] dx = {1, -1, 0, 0};
    int[] dy = {0, 0, 1, -1};

    public void solve(char[][] board) {
        int n = board.length;
        if (n == 0) {
            return;
        }
        int m = board[0].length;
        Queue<int[]> queue = new LinkedList<int[]>();
        for (int i = 0; i < n; i++) {
            if (board[i][0] == 'O') {
                queue.offer(new int[]{i, 0});
                board[i][0] = 'A';
            }
            if (board[i][m - 1] == 'O') {
                queue.offer(new int[]{i, m - 1});
                board[i][m - 1] = 'A';
            }
        }
        for (int i = 1; i < m - 1; i++) {
            if (board[0][i] == 'O') {
                queue.offer(new int[]{0, i});
                board[0][i] = 'A';
            }
            if (board[n - 1][i] == 'O') {
                queue.offer(new int[]{n - 1, i});
                board[n - 1][i] = 'A';
            }
        }
        while (!queue.isEmpty()) {
            int[] cell = queue.poll();
            int x = cell[0], y = cell[1];
            for (int i = 0; i < 4; i++) {
                int mx = x + dx[i], my = y + dy[i];
                if (mx < 0 || my < 0 || mx >= n || my >= m || board[mx][my] != 'O') {
                    continue;
                }
                queue.offer(new int[]{mx, my});
                board[mx][my] = 'A';
            }
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (board[i][j] == 'A') {
                    board[i][j] = 'O';
                } else if (board[i][j] == 'O') {
                    board[i][j] = 'X';
                }
            }
        }
    }
}

Python

class Solution:
    def solve(self, board: List[List[str]]) -> None:
        if not board:
            return
        
        n, m = len(board), len(board[0])
        que = collections.deque()
        for i in range(n):
            if board[i][0] == "O":
                que.append((i, 0))
                board[i][0] = "A"
            if board[i][m - 1] == "O":
                que.append((i, m - 1))
                board[i][m - 1] = "A"
        for i in range(m - 1):
            if board[0][i] == "O":
                que.append((0, i))
                board[0][i] = "A"
            if board[n - 1][i] == "O":
                que.append((n - 1, i))
                board[n - 1][i] = "A"
        
        while que:
            x, y = que.popleft()
            for mx, my in [(x - 1, y), (x + 1, y), (x, y - 1), (x, y + 1)]:
                if 0 <= mx < n and 0 <= my < m and board[mx][my] == "O":
                    que.append((mx, my))
                    board[mx][my] = "A"
        
        for i in range(n):
            for j in range(m):
                if board[i][j] == "A":
                    board[i][j] = "O"
                elif board[i][j] == "O":
                    board[i][j] = "X"

复杂度分析

• 时间复杂度：O(n×m)，其中 n 和 m 分别为矩阵的行数和列数。广度优先搜索过程中，每一个点至多只会被标记一次。
• 空间复杂度：O(n×m)，其中 n 和 m 分别为矩阵的行数和列数。主要为广度优先搜索的队列的开销。