跳跃游戏Ⅳ（bfs+动态规划）

Posted 2021-09-05 秦枫-_-

解题思路：
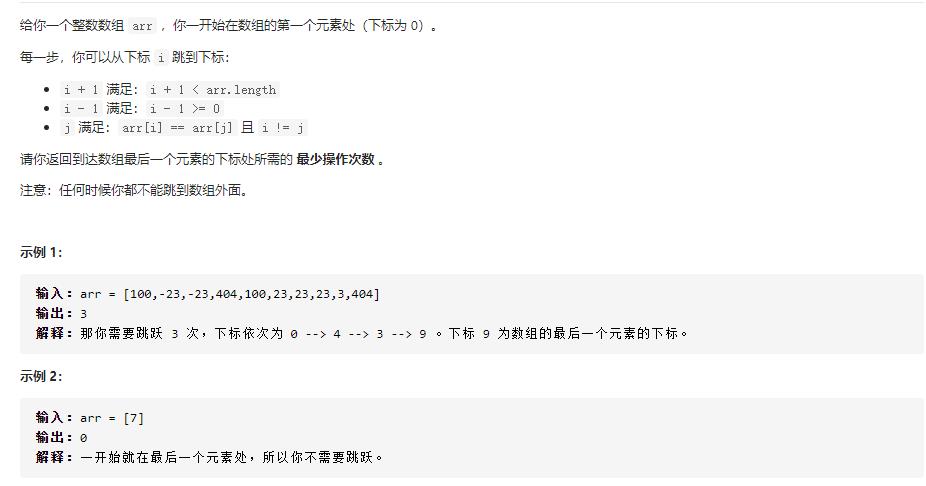
题目要求计算从第一个元素跳到最后一个元素最少的操作次数。首先容易想到的是，坐标位于最后一个元素时，结果应为0，因为不用任何操作；对于这个元素紧挨着的左右元素（此时只存在左边的元素），它的操作数是1，因为只需要跳一次就跳到了最后；同理，对于数组里值和最后一个元素相等的那些数，他们的操作数都是1。
然后，对于倒数第二个元素，它的操作数前一步已经求得为1，它右边数的结果也已经知道了，是0；它左边的数如果不等于最后一个数，那么它跟最后一个数的距离应为2。这里距离的意思是指操作次数，即跳两次才能到达最后一个数；同样，和倒数第二个数相等的那些元素最小的操作数也都是1+1=2.

这样，可以理解为最后一个数所在层数为0，第1层就是挨着它的元素以及值和它相等的那些数，第2层就是第一层挨着的元素以及值和第一层元素相等的那些数…按层次依次往上加。因为题目要求最少操作数，对于“挨着它的元素”如果前面已经求出了距离（层数），这时就不用再去算了，因为+1之后结果只会更大。例如，用一个数组dis[]表示每一个元素对应的最小操作数，初始化一个大数，如果对于元素i它左边有dis[i-1]等于这个大数，就表明i-1位置还没有求，于是dis[i-1]=dis[i]+1;如果dis[i-1]不等于这个大数就说明左边的元素前面已经算过了，就不要再去给它+1。

为了去找数组中和某一个数相等的所有元素位置，使用HashMap来存下所有值和相应位置（列表）的映射，可以避免一遍遍遍历这个数组去寻找。
（这时候你就可以自己动手去写了，小总结：一个数组存结果，一个Map映射和一个队列来广度优先搜索）

现在写出的代码运行那几个试例是没问题的，不过提交的时候会遇到一个满页是7，最后一个数是13的测例，可能会超时。这里还可以继续优化：对于那堆7，从倒数第二个元素开始其实就已经算出了他们的距离是[2,2,…,2,1,0],每次他都会把新出现的7放入队列，然后又遍历一遍7所在的所有位置。于是可以用一个数组visited[]来记录这个数是否被访问（计算）过，如果已经访问过了就没必要再去map里遍历它对应的所有位置了。

class Solution {
    public int minJumps(int[] arr) {
    int n=arr.length;
    Map<Integer,List<Integer>> map=new HashMap<>();
    boolean []pass=new boolean[n];
    int []ans=new int[n];
    Queue<Integer> q=new LinkedList<>();
    q.offer(n-1);
    int inf=Integer.MAX_VALUE;
    Arrays.fill(ans,inf);
    ans[n-1]=0;
    for(int i=0;i<n;i++){
        List<Integer> list=map.getOrDefault(arr[i],new ArrayList<>());
        list.add(i);
        map.put(arr[i],list);//重复值放在一起
    }
    while(!q.isEmpty()){
        int top=q.poll();
        if(top>0&&ans[top-1]==inf){//更新top-1处的值
            ans[top-1]=ans[top]+1;
            q.offer(top-1);
        }
        if(top<n-1&&ans[top+1]==inf){//更新top+1处的值，但是只能用ans[idx]==inf来判断是否更新过，因为这里如果用pass就不会再去查哈希表的重复值因而就缺少很多情况
            ans[top+1]=ans[top]+1;
            q.offer(top+1);
        }
        if(!pass[top]){//避免遇到大量重复值不同位置时重复遍历哈希表
            for(Integer ch:map.get(arr[top])){
                 if(ans[ch]==inf){
                     ans[ch]=ans[top]+1;
                     q.offer(ch);
                     pass[ch]=true;
                 }
            }
        }
    }
    return ans[0];
    }
}