LeetCode 516 最长回文子序列[动态规划] HERODING的LeetCode之路

Posted 2021-09-05 HERODING23

解题思路：
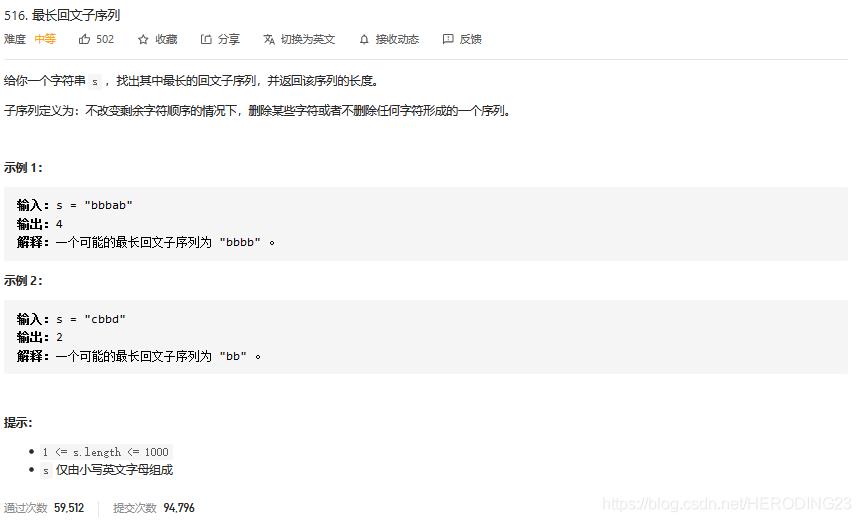
非常经典的一道字符串动态规划题目，首先是dp数组的定义，dp[i][j]代表着从i到j最长回文子序列长度，对于dp[i][i]，每个字符自身就是回文串，长度为1，遍历得从子字符串往整个字符串的方向进行，i 和 j 又代表着子字符串的头尾，所以i要从后往前走，j从i + 1开始往后走，这样才能够满足条件。状态转移方程很好理解，因为 i 和 j 代表着字符串的头尾，如果所指向的字符串相等，那么 dp[i][j] = dp[i + 1][j - 1] + 2;，即子串的最长回文串长度 + 2，如果不相等，那么就取子串中最长的回文串长度，即dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);最后返回dp[0][n - 1]即可，代码如下：

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.length();
        vector<vector<int>> dp(n, vector<int>(n));
        // 从后往前遍历，为了保证i在前，j在后构成一个子字符串进行比较，且从小串往大串发展
        for(int i = n - 1; i >= 0; i --) {
            dp[i][i] = 1;
            char c1 = s[i];
            for(int j = i + 1; j < n; j ++) {
                char c2 = s[j];
                // 相等，更新回文串长度
                if(c1 == c2) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {// 不相等选择最大长度的子回文串长度
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[0][n - 1];
    }
};