python matplotlib pyplot plt.axhline()函数（绘制平行于x轴的水平参考线）

Posted 2021-09-05 Dontla

函数功能：绘制平行于x轴的水平参考线

调用签名：plt.axhline(y=0.0, c="r", ls="--", lw=2)

y：水平参考线的出发点

c：参考线的线条颜色

ls：参考线的线条风格

lw：参考线的线条宽度

平移性：上面的函数，同样适用于axvline()函数

示例：

d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')

import torch
from torch.distributions import multinomial
from d2l import torch as d2l

# 为了抽取⼀个样本，我们只需传⼊⼀个概率向量。输出是另⼀个相同⻓度的向量：它在索引i处的值是采样结果中i出现的次数。
fair_probs = torch.ones([6]) / 6
# print(fair_probs)   # tensor([0.1667, 0.1667, 0.1667, 0.1667, 0.1667, 0.1667])
print(multinomial.Multinomial(1, fair_probs).sample())  # tensor([0., 0., 1., 0., 0., 0.])

# 如果你运⾏采样器很多次，你会发现每次你都得到随机的值。在估计⼀个骰⼦的公平性时，我们经常希望从
# 同⼀分布中⽣成多个样本。如果⽤Python的for循环来完成这个任务，速度会慢得令⼈难以忍受，因此我们使
# ⽤的函数⽀持同时抽取多个样本，返回我们想要的任意形状的独⽴样本数组。
print(multinomial.Multinomial(10, fair_probs).sample())  # tensor([1., 2., 1., 2., 2., 2.])

# 现在我们知道如何对骰⼦进⾏采样，我们可以模拟1000次投掷。然后，我们可以统计1000次投掷后, 每个数字
# 被投中了多少次。具体来说，我们计算相对频率作为真实概率的估计。
# 将结果存储为32位浮点数以进⾏除法
counts = multinomial.Multinomial(1000, fair_probs).sample()
counts = counts / 1000  # 相对频率作为估计值
print(counts)  # tensor([0.1530, 0.1700, 0.1620, 0.1600, 0.1770, 0.1780])
# 因为我们是从⼀个公平的骰⼦中⽣成的数据，我们知道每个结果都有真实的概率1/6，⼤约是0.167，所以上⾯
# 输出的估计值看起来不错。

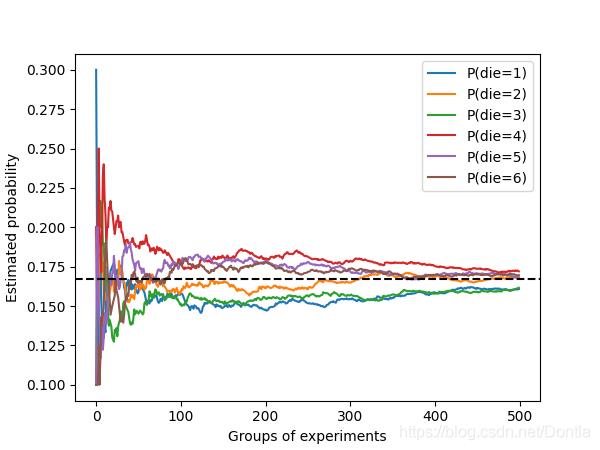
# 我们也可以看到这些概率如何随着时间的推移收敛到真实概率。让我们进⾏500组实验，每组抽取10个样本
counts = multinomial.Multinomial(10, fair_probs).sample((500,))
print(counts.shape)  # torch.Size([500, 6])
cum_counts = counts.cumsum(dim=0)   # 沿指定轴逐级累加

estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)   # 获得概率

# 绘图
d2l.set_figsize((6, 4.5))
for i in range(6):
    # d2l.plt.plot(estimates[:, i].numpy(), label=("P(die=" + str(i + 1) + ")"))
    d2l.plt.plot(estimates[:, i], label=("P(die=" + str(i + 1) + ")"))  # 转不转换成numpy数组都行
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend()
d2l.plt.show()

运行结果：

参考文章：python可视化—axhline()函数