深度学习中Transformer的原理和方法（李宏毅视频课笔记）
Posted Y_蒋林志
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了深度学习中Transformer的原理和方法（李宏毅视频课笔记）相关的知识，希望对你有一定的参考价值。
文章目录
0 前言
本节学习的是Transformer。Google于2017年6月发布在arxiv上的一篇文章《Attention is all you need》，提出解决sequence to sequence问题的transformer模型，用全self-attention的结构代替了lstm，这也是现在主流的BERT模型的基础。本文由整理李宏毅老师视频课笔记和个人理解所得，详细讲述了Transformer的原理及实现方法。我会及时回复评论区的问题，如果觉得本文有帮助欢迎点赞 😃。
1 RNN to CNN
一般常用的就是RNN，输入是一串Vector Sequence，输出也是一串Vector Sequence。RNN常用于处理输入是有序的情况，但是RNN有问题——不易被平行化（并行运算）。如图，就单向RNN而言，当仅需要输出
b
4
b^4
b4时，则需要等候
a
1
,
a
2
,
a
3
,
a
4
a^1, a^2, a^3, a^4
a1,a2,a3,a4的输入。即使是双向的RNN，
b
1
,
b
2
,
b
3
,
b
4
b^1, b^2, b^3, b^4
b1,b2,b3,b4也不能同时计算：
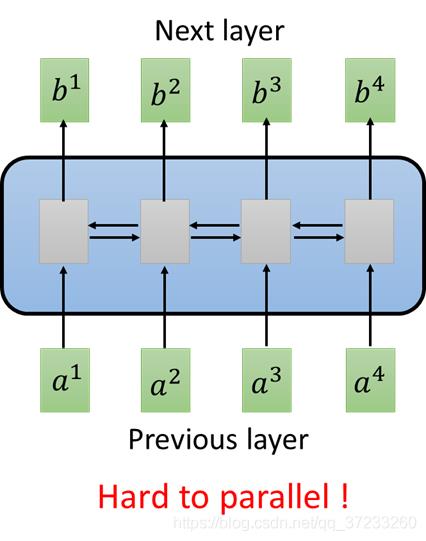
所以有人想使用CNN来代替RNN，输入不变，三角形代表是一个Filter（不止一个），以3个向量为一组进行扫描。多使用几组Filter也可以做到，输入是一个Sequence，对应输出是一个Sequence：
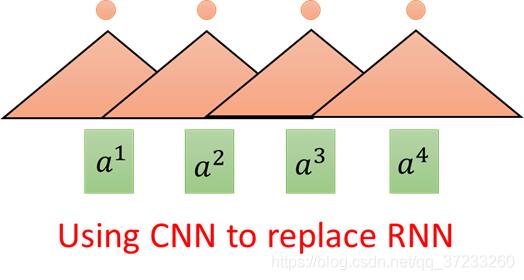
表面上CNN和RNN一样，但是一层CNN的一个输出只考虑三个输入的Vector，但是RNN（双向的）却要考虑整个句子。所以考虑增加CNN的层数，这样就是可以使得感受野增大，即可以考虑所有的输入。CNN的好处是可以平行化，每一个Filter（三角形）都可以单独运算，并不需要等之前或者之后的Filter计算结束。
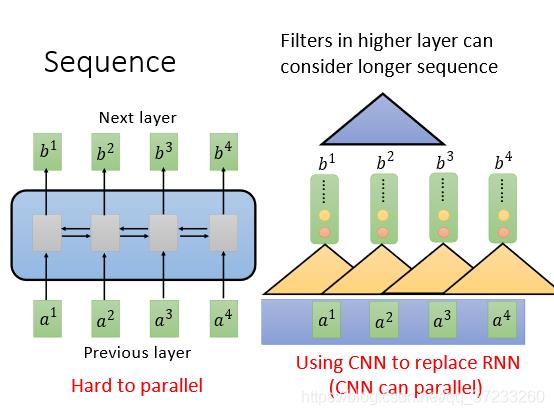
2 Self-Attention
2.1 Base Method
CNN需要叠很多层，如果只要求一层就要获得所有输入的信息怎么做呢？这里就是引入Self-Attention Layer，可以完美替代双向RNN：
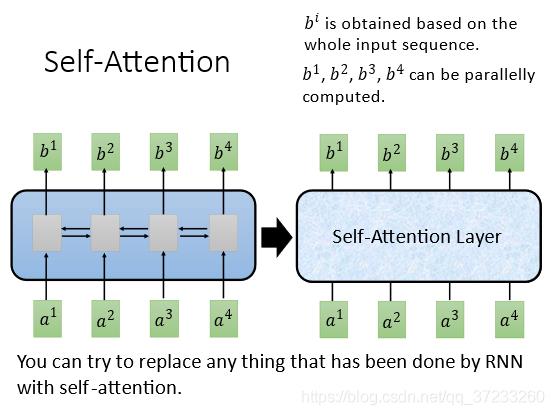
输入是
x
i
x^i
xi，通过一个embedding（映射）W矩阵得到
a
i
a^i
ai，然后将
a
i
a^i
ai输入到self-attention layer，分别乘上三个不同的变换，获得三个不同的vector，即
q
i
,
k
i
,
v
i
q^i,k^i,v^i
qi,ki,vi，代表不同的三种意思：
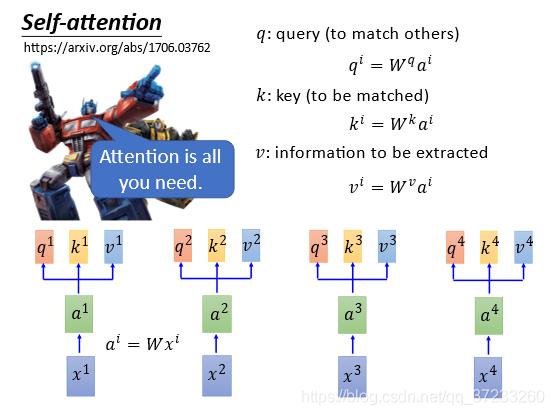
接下来要做拿每一个query
q
q
q去对每一个key
k
k
k做attention（4对4），以
q
1
q^1
q1为例，如下图，得到4个attention：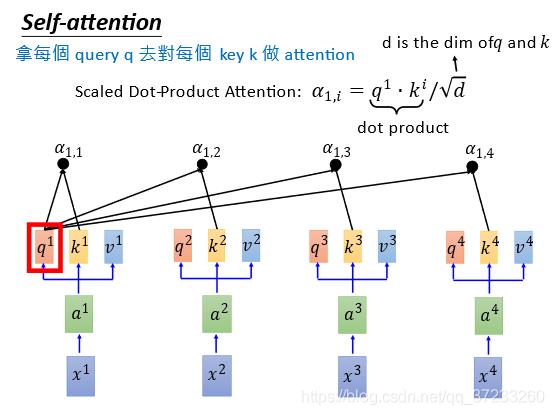 
我们已知attention的本质就是匹配度，那么就需要定义匹配度的计算：
α
1
,
i
=
q
1
⋅
k
i
/
d
\\alpha_{1, i}=q^{1} \\cdot k^{i} / \\sqrt{d}
α1,i=q1⋅ki/d
其中d是
q
q
q和
k
k
k的维度。关于除以
d
\\sqrt{d}
d有个这样的解释：
q
q
q和
k
k
k的内积的值和维度d大小关系很大，这样除了之后方差就会为1了。当然定义别的匹配度也可以。
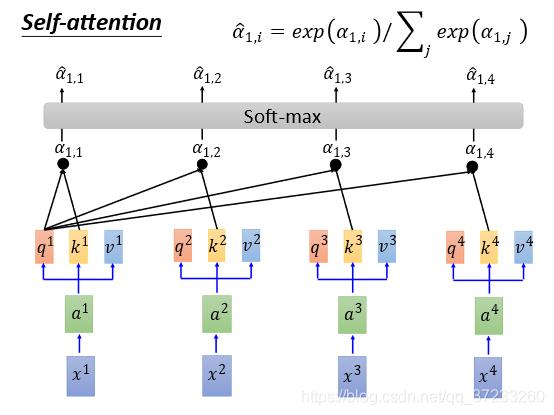
接下来通过一个Softmax Layer得到对应的概率值
α
^
1
,
1
α
^
1
,
2
α
^
1
,
3
α
^
1
,
4
\\begin{array}{llll}\\hat{\\alpha}_{1,1} & \\hat{\\alpha}_{1,2} & \\hat{\\alpha}_{1,3} & \\hat{\\alpha}_{1,4}\\end{array}
α^1,1α^1,2α^1,3α^1,4：
将
α
^
1
,
1
α
^
1
,
2
α
^
1
,
3
α
^
1
,
4
\\begin{array}{llll}\\hat{\\alpha}_{1,1} & \\hat{\\alpha}_{1,2} & \\hat{\\alpha}_{1,3} & \\hat{\\alpha}_{1,4}\\end{array}
α^1,1α^1,2α^1,3α^1,4与各自的
v
v
v相乘之后相加（
b
1
=
∑
i
α
^
1
,
i
v
i
b^{1}=\\sum_{i} \\hat{\\alpha}_{1, i} v^{i}
b1=∑iα^1,ivi 等价于weight sum），得到一个向量
b
1
b^1
b1：
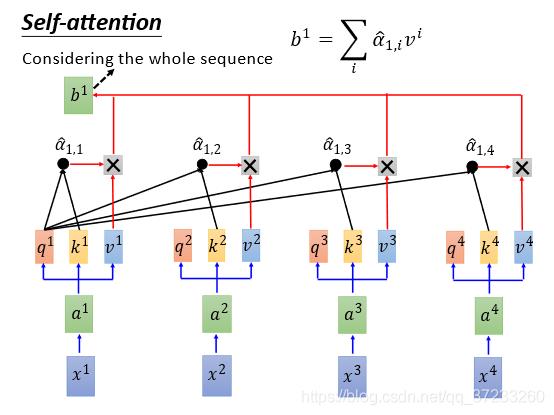
这样Self-Attention就输出一个vector，而且产生这个
b
1
b^1
b1已经考虑了所有输入的信息，如果只想考虑local的信息，只需要将
α
^
1
,
1
α
^
1
,
2
α
^
1
,
3
α
^
1
,
4
\\begin{array}{llll}\\hat{\\alpha}_{1,1} & \\hat{\\alpha}_{1,2} & \\hat{\\alpha}_{1,3} & \\hat{\\alpha}_{1,4}\\end{array}
α^1,1α^1,2α^1,3α^1,4中不需要的变成0就可以了。需要什么信息，就获取什么信息。
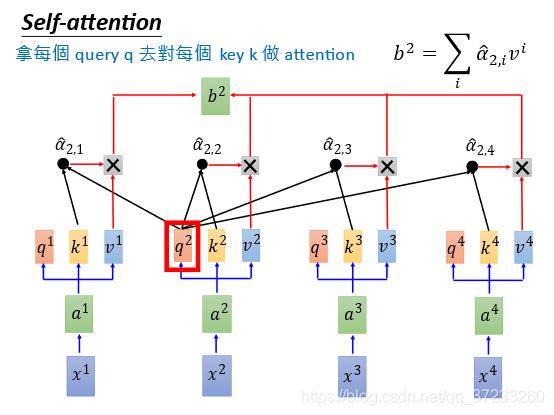
因为信息是已知的，在同一个时间如下图可以计算
b
2
b^2
b2，并不冲突：
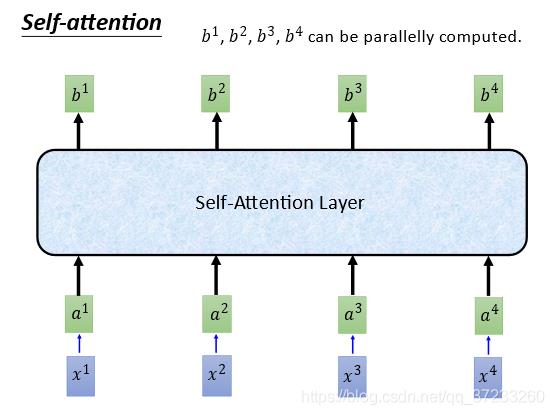
总而言之，输入了
x
1
,
x
2
,
x
3
,
x
4
x^1, x^2, x^3 ,x^4
x1,x2,x3,x4，输出了
b
1
,
b
2
,
b
3
,
b
4
b^1, b^2, b^3, b^4
b1,b2,b3,b4，和RNN做了一样的工作，但是可以平行计算的：
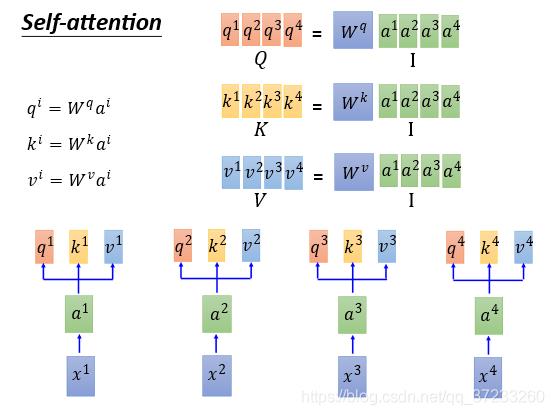
2.2 Matrix Representation
接下来用矩阵的形式表述Self-Attention是怎么做平行化的。将所有的
q
q
q收集起来作为一个
Q
Q
Q矩阵，每一列作为一个
q
q
q，同理可以得到其他的矩阵：
接下来表述 α i , j \\alpha_{i,j} αPyTorch深度学习项目实战100例—— 基于Transformer实现Twitter文本隐喻二分类 | 第43例