论文|SDNE的算法原理代码实现和在阿里凑单场景中的应用说明
Posted 搜索与推荐Wiki
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了论文|SDNE的算法原理代码实现和在阿里凑单场景中的应用说明相关的知识,希望对你有一定的参考价值。
1.概述
SDNE(Structural Deep Network Embedding)算法是发表在KDD-2016上的一篇文章,论文的下载地址为:https://www.kdd.org/kdd2016/papers/files/rfp0191-wangAemb.pdf
SDNE主要也是用来构建node embedding的,和之前介绍的node2vec发表在同年,但不过node2vec可以看作是deepwalk的扩展,而SDNE可以看作是LINE的扩展。
2.算法原理
SDNE和LINE中相似度的定义是一致的,同样是定义了一阶相似度和二阶相似度,一阶相似度衡量的是相邻的两个顶点对之间相似性,二阶相似度衡量的是,两个顶点他们的邻居集合的相似程度。
模型结构 如下:
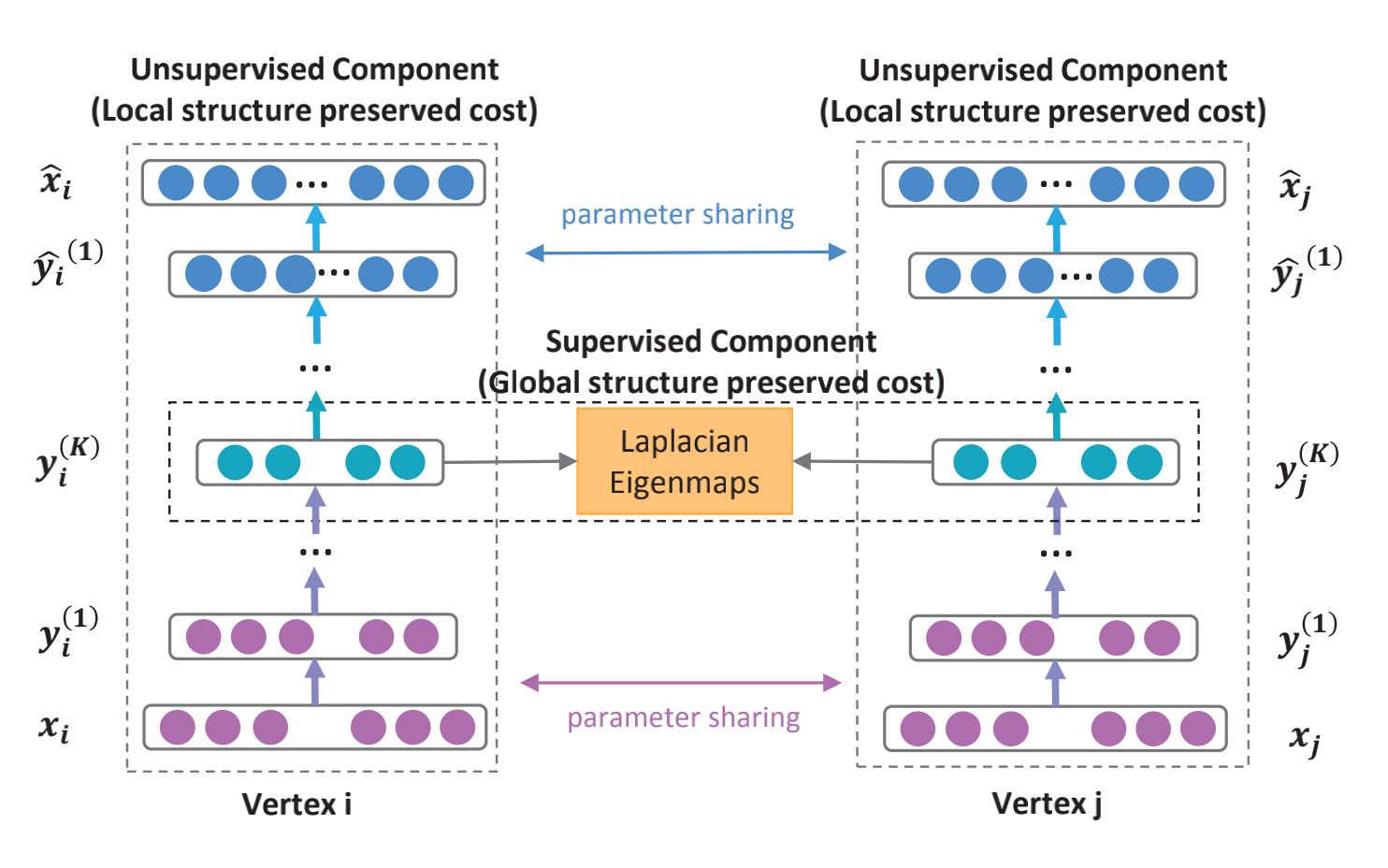
模型主要包括两个部分:无监督和有监督部分,其中:
- 无监督部分是一个深度自编码器用来学习二阶相似度(上图中两侧部分)
- 监督部分是一个拉普拉斯特征映射捕获一阶相似度(中间的橘黄色部分)
对于一阶相似度,损失函数定义如下:
L
1
s
t
=
∑
i
,
j
=
1
s
i
,
j
∥
y
i
K
−
y
j
K
∥
2
2
=
∑
i
,
j
=
1
s
i
,
j
∥
y
i
−
y
j
∥
2
2
L_{1st}=\\sum_{i,j=1}s_{i,j} \\left \\| y_i^K - y_j^K \\right \\| _{2}^{2} = \\sum_{i,j=1}s_{i,j} \\left \\| y_i - y_j \\right \\| _{2}^{2}
L1st=i,j=1∑si,j∥∥yiK−yjK∥∥22=i,j=1∑si,j∥yi−yj∥22
该损失函数可以让图中的相邻的两个顶点对应的embedding vector在隐藏空间接近。
论文中还提到一阶相似度的损失函数还可以表示为:
L
1
s
t
=
∑
i
,
j
=
1
s
i
,
j
∥
y
i
−
y
j
∥
2
2
=
2
t
r
(
Y
T
L
Y
)
L_{1st}=\\sum_{i,j=1}s_{i,j} \\left \\| y_i - y_j \\right \\| _{2}^{2} = 2tr(Y^TLY)
L1st=i,j=1∑si,j∥yi−yj∥22=2tr(YTLY)
其中:
- L L L 是图对应的拉普拉斯矩阵
- L = D − S L = D - S L=D−S, D D D 是图中顶点对应的度矩阵, S S S 是邻接矩阵, D i , i = ∑ j s i , j D_{i,i} = \\sum_{j}s_{i,j} Di,i=∑jsi,j
拉普拉斯矩阵是「图论」中重要的知识点,可以参考:https://blog.csdn.net/qq_30159015/article/details/83271065,查看更清晰的介绍
对于二阶相似度,损失函数定义如下:
L
2
n
d
=
∑
i
n
∥
x
i
^
−
x
i
∥
2
2
L_{2nd} = \\sum_{i}^{n} \\left \\| \\hat{x_i} - x_i \\right \\| _{2}^{2}
L2nd=i∑n∥xi^−xi∥22
这里使用图的邻接矩阵进行输入,对于第
i
i
i 个顶点,有
x
i
=
s
i
x_i = s_i
xi=si ,每一个
s
i
s_i
si 都包含了顶点
i
i
i 的邻居结构信息,所以这样的重构过程能够使得结构相似的顶点具有相似的embedding表示向量。
但是现实中由于图都是稀疏的,邻接矩阵
S
S
S 中的非零元素是远远少于零元素的,那么对于神经网络来说只要全部输出0也能取得一个不错的效果,这不是我们想要的。为了解决这个问题,论文提出一种使用带权损失函数,对于非零元素具有更高的惩罚系数。 修正后的损失函数为:
L
2
n
d
=
∑
i
n
∥
(
x
i
^
−
x
i
)
⊙
b
i
∥
2
2
=
∥
(
X
i
^
−
X
i
)
⊙
B
∥
F
2
L_{2nd} = \\sum_{i}^{n} \\left \\| (\\hat{x_i} - x_i) \\odot b_i \\right \\| _{2}^{2} = \\left \\| (\\hat{X_i} - X_i) \\odot B \\right \\| _{F}^{2}
L2nd=i∑n∥(xi^−xi)⊙bi∥22=∥∥∥(Xi^−Xi)⊙B∥∥∥F2
其中:
- ⊙ \\odot ⊙ 为逐元素积
- b i = { b i , j } j = 1 n b_i = \\left \\{ b_{i,j} \\right \\}_{j=1}^{n} bi={bi,j}j=1n,若 s i , j = 0 s_{i,j}=0 si,j=0,则 b i , j = 1 b_{i,j}=1 bi,j=1,否则 b i , j = β > 1 b_{i,j} = \\beta >1 bi,j=β>1
模型整体的优化目标为:
L
m
i
x
=
α
L
1
s
t
+
L
2
n
d
+
v
L
r
e
g
L_{mix} = \\alpha L_{1st} + L_{2nd} + v L_{reg}
Lmix=αL1st+