2021杭电多校赛2021“MINIEYE杯”中国大学生算法设计超级联赛签到题5题
Posted 小哈里
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2021杭电多校赛2021“MINIEYE杯”中国大学生算法设计超级联赛签到题5题相关的知识,希望对你有一定的参考价值。
Solved Pro.ID Title Ratio(Accepted / Submitted)
1001 Fall with Fake Problem 3.45%(3/87)
1002 Fall with Soldiers 28.57%(8/28)
1003 Fall with Trees 23.77%(618/2600) 结论,推公式
1004 Link with Balls 43.45%(179/412)
1005 Link with EQ 69.82%(303/434)
1006 Link with Grenade 43.55%(206/473)
1007 Link with Limit 16.21%(490/3022)建图,找环
1008 Smzzl with Greedy Snake 57.28%(527/920) 小模拟
1009 Smzzl with Safe Zone 5.48%(12/219)
1010 Smzzl with Tropical Taste 53.36%(898/1683) 签到,判断
1011 Yiwen with Formula 12.73%(76/597)
1012 Yiwen with Sqc 32.05%(483/1507)统计贡献,差分优化
1003 Fall with Trees
题意:
- 在二维平面坐标系中,给出根节点和左右子节点的坐标,按照规范画k层二叉树并求凸包面积。
- 规范为:子节点横坐标关于父节点对称,高度相等,左子树小于右子树。
思路:
- 2e5个询问,很容易想到是个结论题,所以推公式,需要注意输出的精度。
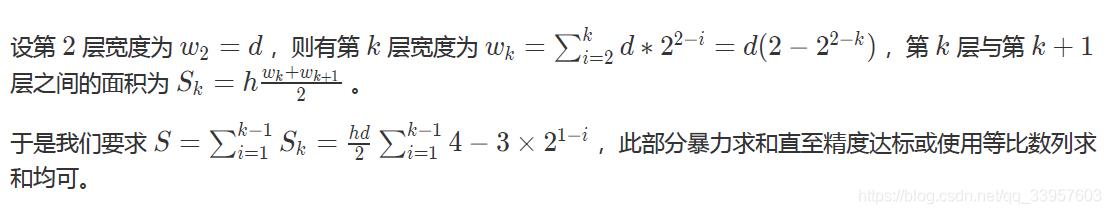
#include<bits/stdc++.h>
using namespace std;
int main(){
int T; scanf("%d", &T);
while(T--){
int k; scanf("%d", &k);
double px, py, lx, ly, rx, ry;
scanf("%lf%lf%lf%lf%lf%lf",&px,&py,&lx,&ly,&rx,&ry);
double x = (rx-lx)/2, y = py-ly;
double ans = x*y*(4*k-10+3.0/pow(2,k-2));
//cout<<fixed<<setprecision(3)<<ans<<"\\n";
printf("%.3f\\n", ans);
}
return 0;
}
1007 Link with Limit
题意:
- 给出f[1]到f[n], 定义f1[x]=f[x], fn[x]=f[f{n-1}[x]].
- 定义g(x)=sum{fi[x], 1<=i<=∞}, 判断x=[1,n]时g(x)是否满足都相等, x,n<=1e5
思路:
- 开始看错题了,以为g(x)是1-n的,就在想怎么优化预处理出所有的f数组,后来意识到∞才知道方向错了,需要往数学方面想,又绕了一段时间,意识到1e5的数据可能是图论或数据结构。
- 建图,点 x 向点 f(x) 连边,那么迭代的过程实质上是在图上行走的过程。原题实际上问的是每一个环的点权平均值是否相同,使用任意方法找出所有环并求出平均值即可。
- 扔一个好多年前不知道多久没用过的kosaraju板子跑出了所有强连通分量,注意统计的时候需要考虑,如样例“2 1 1”,2是连向1的自环,2虽然是联通分量但是它本身不算环,需要加一条特判一下有没有连向自己的边。同时在比较平均值是否相等的时候,为了防止除法精度的问题,可以采用比较当前与下一个分子分母错位相乘结果的方式。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 2e5+10;
//kosaraju
vector<int>G[maxn], rG[maxn];
vector<int>vs, cmp[maxn];
int vis[maxn], book[maxn], cnt;
void dfs(int u){
if(vis[u])return ;
vis[u] = 1;
for(int to: G[u])dfs(to);
vs.push_back(u);
}
void rdfs(int u){
book[u] = cnt;
cmp[cnt].push_back(u);
for(int to: rG[u])if(!book[to])rdfs(to);
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int T; cin>>T;
while(T--){
int n; cin>>n;
vs.clear(); cnt = 0;
for(int i = 1; i <= n; i++)G[i].clear(),rG[i].clear(),cmp[i].clear(),vis[i]=book[i]=0;
for(int i = 1; i <= n; i++){
int fi; cin>>fi;
G[i].push_back(fi); rG[fi].push_back(i);
}
for(int i = 1; i <= n; i++)dfs(i);
for(int i = n-1; i >= 0; i--){
if(!book[vs[i]]){
++cnt;
rdfs(vs[i]);
}
}
int ok = 1;
for(int i = 1; i+1 <= cnt; i++){
double sum = 0, sum2=0;
if(cmp[i].size()==1 && G[cmp[i][0]][0]!=cmp[i][0]){//特判
continue;
}
for(int x:cmp[i]) sum += x;
for(int x:cmp[i+1])sum2+=x;
if(sum*cmp[i+1].size()!=sum2*cmp[i].size()){//比较
ok = 0; break;
}
}
if(ok==1)cout<<"YES\\n";
else cout<<"NO\\n";
}
return 0;
}
1008 Smzzl with Greedy Snake
题意:
- 给出n个食物及其坐标,必须按顺序吃掉全部,保证方案存在。
- 从(x,y)出发,沿着d方向,每次可以前进或顺时针逆时针转弯,用时都为1,求构造用时最少的方案。
思路:
- 因为要按顺序吃,所以可以贪心在当前吃完的地方直接直线+转弯+直线的方式吃掉下一个,直接模拟就好。
- 注意到如果当前和下一个要吃的食物是对角线时,当前方向如果与某个方向一致,那需要先走这个方向,实际写的时候可以直接两个都跑一遍选最短即可。
#include<bits/stdc++.h>
using namespace std;
string go(int x, int y, int &d, int sx, int sy){
string s1="";
if(sx<x && d!=3){
if(d==0)s1+='u';
if(d==2)s1+='c';
if(d==1)s1+="uu";
d=3;
}
if(sx>x && d!=1){
if(d==0)s1+='c';
if(d==2)s1+='u';
if(d==3)s1+="uu";
d=1;
}
s1 += string(abs(sx-x), 'f');
if(sy<y && d!=2){
if(d==0)s1+="cc";
if(d==1)s1+='c';
if(d==3)s1+='u';
d=2;
}
if(sy>y && d!=0){
if(d==1)s1+='u';
if(d==2)s1+="uu";
if(d==3)s1+='c';
d=0;
}
s1 += string(abs(sy-y), 'f');
return s1;
}
string go2(int x, int y, int &d, int sx, int sy){
string s1="";
if(sy<y && d!=2){
if(d==0)s1+="cc";
if(d==1)s1+='c';
if(d==3)s1+='u';
d=2;
}
if(sy>y && d!=0){
if(d==1)s1+='u';
if(d==2)s1+="uu";
if(d==3)s1+='c';
d=0;
}
s1 += string(abs(sy-y), 'f');
if(sx<x && d!=3){
if(d==0)s1+='u';
if(d==2)s1+='c';
if(d==1)s1+="uu";
d=3;
}
if(sx>x && d!=1){
if(d==0)s1+='c';
if(d==2)s1+='u';
if(d==3)s1+="uu";
d=1;
}
s1 += string(abs(sx-x), 'f');
return s1;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int T; cin>>T;
while(T--){
int x, y, d; cin>>x>>y>>d;
int n; cin>>n;
string ans = "";
for(int i = 1; i <= n; i++){
int sx, sy; cin>>sx>>sy;
int d1=d, d2=d;
string t1= go(x,y,d1,sx,sy);
string t2= go2(x,y,d2,sx,sy);
if(t1.size()<t2.size())ans+=t1,d=d1;
else ans+=t2,d=d2;
x = sx, y = sy;
}
cout<<ans<<"\\n";
}
return 0;
}
1010 Smzzl with Tropical Taste
题意:
- 一个游泳池,开始有V升冰红茶,店主每秒加入qV升,男孩喝每秒pV升,判断男孩能否喝到G升。(G取任意正整数)
思路:
- 只要加入的比喝的快就行,即q>=p。
#include<bits/stdc++.h>
using namespace std;
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int T; cin>>T;
while(T--){
double p, q; cin>>p>>q;
if(q>=p)cout<<"N0 M0R3 BL4CK 1CE TEA!\\n";
else cout<<"ENJ0Y YOURS3LF!\\n";
}
return 0;
}
1012 Yiwen with Sqc
题意:
- 给出一个字符串,计算每个字母在每个区间出现次数的平方和。
思路:
- 可以发现不同字母之间没有影响,所以分别考虑每一种字母,比如考虑 ‘a’ , ‘a’ 在字符串中一共出现cnt次,第i次的位置为 p[i](p[0]=0, p[cnt+1]=n+1),记len[i] = p[i+1]-p[i],即两个相邻 ‘a’ 之间的距离。
- 首先固定左端点为1,移动右端点,可以发现答案=sum{k=1->cnt, len[k]*k^2},因为右端点在两个字母间移动时字母数量不变,对答案贡献也不变,可以直接累加。然后固定右端点,移动左端点,可以发现对于p[i]到p[i+1]之间的位置,答案为 sum{ k=i+1->cnt, len[k]*(k-i)^2}。
- 考虑维护两次差分对复杂度进行优化,最后O(n)可以通过。


#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int mod = 998244353;
int calc(vector<int>vc){
int ans = 0, per = 0, dif = 0;
for(int i = 1; i < vc.size(); i++){
ans = (1ll*ans+1ll*per*(vc[i]-vc[i-1]))%mod;
dif = (1ll*dif+2ll*vc[i-1]+vc[i]-vc[i-1])%mod;
per = (per+dif)%mod;
}
return ans;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int T; cin>>T;
while(T--){
string s; cin>>s; s="1"+s;
int n = s.size()-1;
vector<int>vc[30];
for(int i = 0; i <= 25; i++)vc[i].push_back(0);
for(int i = 1; i <= n; i++)vc[s[i]-'a'].push_back(i);
for(int i = 0; i <= 25; i++)vc[i].push_back(n+1);
int ans = 0;
for(int i = 0; i <= 25; i++)
ans = (ans+calc(vc[i]))%mod;
cout<<ans<<"\\n";
}
return 0;
}
以上是关于2021杭电多校赛2021“MINIEYE杯”中国大学生算法设计超级联赛签到题5题的主要内容,如果未能解决你的问题,请参考以下文章