（动态规划）1547. 切棍子的最小成本（区间dp）/221. 最大正方形 / 1312. 让字符串成为回文串的最少插入次数（区间dp）

Posted 2021-09-04 Zephyr丶J

1547. 切棍子的最小成本

题目描述

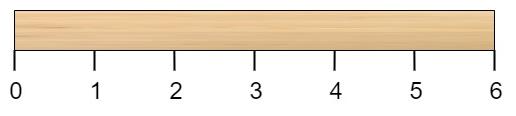
有一根长度为 n 个单位的木棍，棍上从 0 到 n 标记了若干位置。例如，长度为 6 的棍子可以标记如下：

给你一个整数数组 cuts ，其中 cuts[i] 表示你需要将棍子切开的位置。

你可以按顺序完成切割，也可以根据需要更改切割的顺序。

每次切割的成本都是当前要切割的棍子的长度，切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍（这两根木棍的长度和就是切割前木棍的长度）。请参阅第一个示例以获得更直观的解释。

返回切棍子的 最小总成本 。

示例 1：

输入：n = 7, cuts = [1,3,4,5]
输出：16
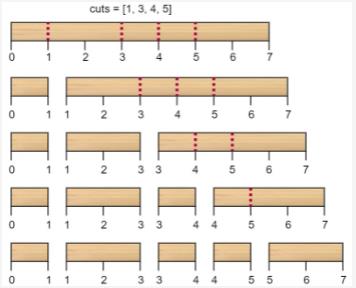
解释：按 [1, 3, 4, 5] 的顺序切割的情况如下所示：

第一次切割长度为 7 的棍子，成本为 7 。第二次切割长度为 6 的棍子（即第一次切割得到的第二根棍子），第三次切割为长度 4 的棍子，最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。
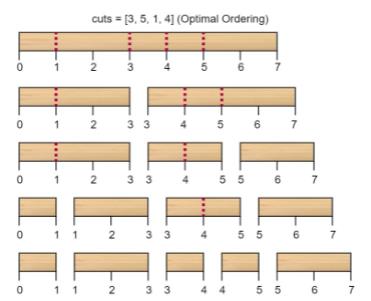
而将切割顺序重新排列为 [3, 5, 1, 4] 后，总成本 = 16（如示例图中 7 + 4 + 3 + 2 = 16）。

示例 2：

输入：n = 9, cuts = [5,6,1,4,2]
输出：22
解释：如果按给定的顺序切割，则总成本为 25 。总成本 <= 25 的切割顺序很多，例如，[4, 6, 5, 2, 1] 的总成本 = 22，是所有可能方案中成本最小的。

提示：
2 <= n <= 10^6
1 <= cuts.length <= min(n - 1, 100)
1 <= cuts[i] <= n - 1
cuts 数组中的所有整数都 互不相同

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-cost-to-cut-a-stick
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

区间dp，学习

class Solution {
    public int minCost(int n, int[] cuts) {
        //区间dp
        //dp[i][j]表示表示在当前待切割的木棍的左端点为cuts[i]，右端点为cuts[j] 时，将木棍全部切开的最小总成本。
        //那么怎么更新呢，
        //首先在左右两端各加一个切割点，0和n
        //在dp[i][j]内共有cut[i + 1],cut[i + 2]...cut[j - 1]个切割点，枚举这些切割点，可以将木棍分成更小的部分
        //dp[i][j] = dp[i][k] + dp[k][j] + len;
        //也就是子问题

        int m = cuts.length;
        //对cuts数组排序，即对切割点进行排序
        Arrays.sort(cuts);
        //加开头和结尾两个点，复制到新的数组中
        int[] cutss = new int[m + 2];

        cutss[0] = 0;
        cutss[m + 1] = n;

        System.arraycopy(cuts, 0, cutss, 1, m);

        int[][] dp = new int[m + 2][m + 2];
        //相邻两个点切割成本为0
        dp[0][0] = 0;
        for(int i = 1; i < m + 2; i++){
            dp[i][i] = 0;
            dp[i - 1][i] = 0;
        }
        
        //因为根据更新规则，i依赖于比它大的，j依赖于比它小的，所以i从大大小遍历，j从小到大
        for(int i = m; i >= 0; i--){
            for(int j = i + 2; j < m + 2; j++){
                //如果i和j相等，那么只有一个切割点，
                dp[i][j] = Integer.MAX_VALUE;
                //遍历所有的分割点
                for(int k = i + 1; k < j; k++){
                    dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j]);
                }
                dp[i][j] += cutss[j] - cutss[i];
            }
        }
        return dp[0][m + 1];
    }
}

221. 最大正方形

题目描述

在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。

示例 1：

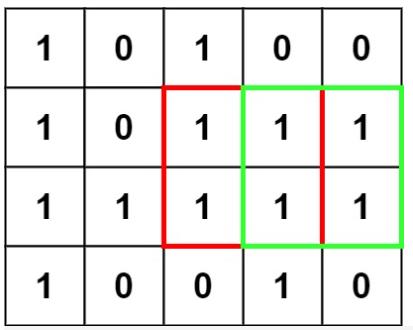
输入：matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出：4

示例 2：

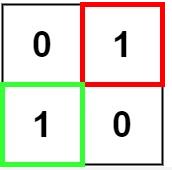
输入：matrix = [[“0”,“1”],[“1”,“0”]]
输出：1

示例 3：

输入：matrix = [[“0”]]
输出：0

提示：
m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] 为 ‘0’ 或 ‘1’

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximal-square
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

只能想到用前缀和处理面积，然后遍历开始位置和正方形边长，根据前缀和处理面积是否等于边长的平方
怎么动态规划呢？

class Solution {
    public int maximalSquare(char[][] matrix) {
        //我能想到的就是矩阵的前缀和，然后遍历开始位置和正方形的边长大小，确定一个最大的正方形
        //就和牛客模拟笔试那个题一样

        //怎么动态规划呢
        //dp[i][j]表示以(i,j)为右下角，最大的正方形边长
        //此时，和dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]有关系，
        //就等于三者的最小值，加1
        //因为如果想要扩展这个正方形的边长，那么这三个值，肯定都得是一样的，否则，只能由最小的来表示当前的正方形
        
        int m = matrix.length;
        int n = matrix[0].length;

        int[][] dp = new int[m + 1][n + 1];
        int max = 0;
        for(int i = 1; i <= m; i++){
            for(int j = 1; j <= n; j++){
                if(matrix[i - 1][j - 1] == '0'){
                    dp[i][j] = 0;
                    continue;
                }
                dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
                max = Math.max(max, dp[i][j]);
            }
        }
        return max * max;
    }
}

1312. 让字符串成为回文串的最少插入次数

这周力扣推荐的题

题目描述

给你一个字符串 s ，每一次操作你都可以在字符串的任意位置插入任意字符。

请你返回让 s 成为回文串的 最少操作次数 。

「回文串」是正读和反读都相同的字符串。

示例 1：

输入：s = “zzazz”
输出：0
解释：字符串 “zzazz” 已经是回文串了，所以不需要做任何插入操作。

示例 2：

输入：s = “mbadm”
输出：2
解释：字符串可变为 “mbdadbm” 或者 “mdbabdm” 。

示例 3：

输入：s = “leetcode”
输出：5
解释：插入 5 个字符后字符串变为 “leetcodocteel” 。

示例 4：

输入：s = “g”
输出：0

示例 5：

输入：s = “no”
输出：1

提示：

1 <= s.length <= 500
s 中所有字符都是小写字母。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-insertion-steps-to-make-a-string-palindrome
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

一眼望去就是动规

class Solution {
    public int minInsertions(String s) {
        //dp[i][j]表示i到j成为回文串的最小操作次数
        //如果s[i]和s[j]相同，那么就是dp[i + 1][j - 1]
        //如果不同，那么就需要添加一个字符，可以添加在开头，也可以添加在结尾，即考虑dp[i + 1][j]（添加在了末尾）
        //或者dp[i][j - 1]（添加在了开头）
        
        int l = s.length();
        int[][] dp = new int[l][l];

        //i依赖于i+1，j依赖于j-1
        for(int i = l - 2; i >= 0; i--){
            for(int j = i + 1; j < l; j++){
                if(s.charAt(i) == s.charAt(j))
                    dp[i][j] = dp[i + 1][j - 1];
                else{
                    dp[i][j] = Math.min(dp[i][j - 1] + 1, dp[i + 1][j] + 1);
                }
            }
        }
        return dp[0][l - 1];
    }
}

或者还可以这样想，也就是官解1的做法：
题目表示求让一个字符串变为回文串的最少插入操作，意思就是这个字符串里面最长的回文子序列的长度是多少，其他字符要形成回文需要对称的添加；所以用字符串长度减去最长回文子序列即可
这个不太好理解