自学笔记-线段树（21.8.9）

Posted 2021-09-04 未定_

线段树（一）
三.区间修改
1.在线段树的基础上增加了以下操作：
•区间[i,j]内的值全部加v
•计算区间[l,r]的区间和
为了节省时间，采取lazy原理，即树上某一结点的区间全部在[i,j]范围内，只需要对该结点的区间值全部加v，不需要继续深入对每一个数改变；如果树上某一结点的区间有部分在[i,j]范围内，不能再用lazy，需继续深入直到全部在范围内。图解：以1～10为例，把区间[3,6]每个元素加3。

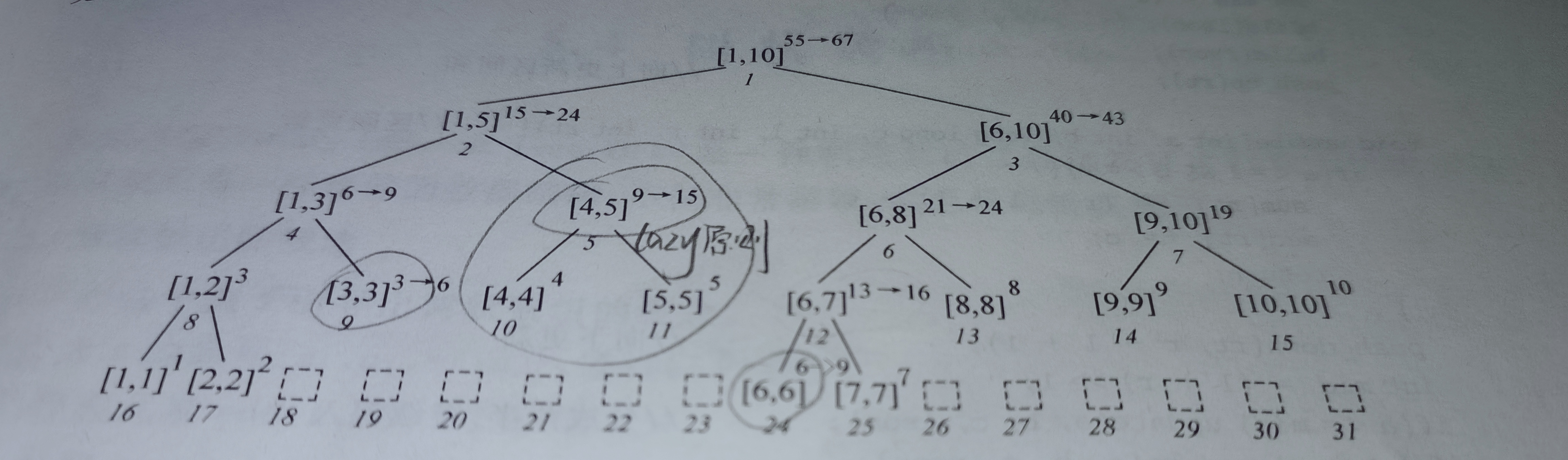
为了用lazy原理，需要增加一个数组add[i]来记录，其值为每个元素需要增加的值，多次lazy也可以累加。如果某结点lazy被破坏，则需要深入(向下更新)，该结点add归0，表示没有lazy，更新子结点，这里通常自写向下更新函数push_down( )实现该功能。

2.建树： 可以用满二叉树建树：以1～10为例

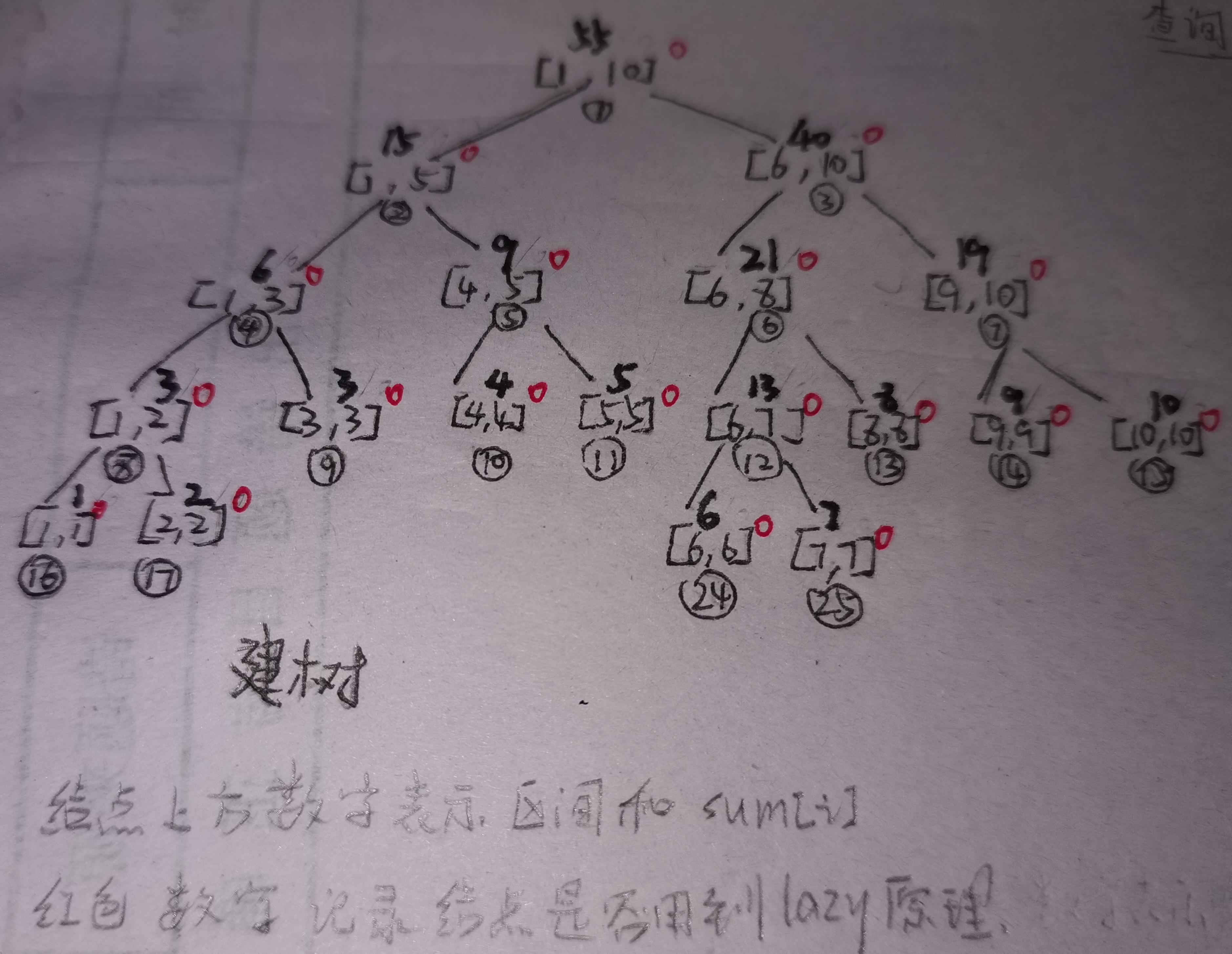
结点上方区间和用sum[]表示，右上方红色记录是否用到lazy原理，即add[]

void build(int l,int r,int rt)//满二叉树建树
{
    add[rt]=0;
    if(l==r)
    {
        scanf("%lld",&sum[rt]);
        return;
    }
    int mid=(l+r)>>1;
    build(lson);
    build(rson);
    push_up(rt);//向上更新区间和
}

3.向上更新函数与向下更新函数
向上更新函数用于把子结点的值递归到父结点，更新区间并求区间和时需要用到；向下更新函数用于碰坏lazy，更新子结点。

void push_up(int rt)//向上更新，通过当前结点rt把值递归到父结点
{
    sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}
void push_down(int rt,int m)//更新rt的子结点,m为区间数字的个数
{
    if(add[rt])
    {
        add[rt<<1]+=add[rt];//左儿子累加
        add[rt<<1|1]+=add[rt];//右儿子累加
        sum[rt<<1]+=(m-(m>>1))*add[rt];//左儿子区间总和变化
        sum[rt<<1|1]+=(m>>1)*add[rt];//右儿子区间总和变化
        add[rt]=0;//取消本层标记
    }
}

4.区间更新
对区间[a,b]内的每一个元素加c，[l,r]为查询区间

void update(int a,int b,long long c,int l,int r,int rt)
{
    if(a<=l&&b>=r)
    {
        sum[rt]+=(r-l+1)*c;
        add[rt]+=c;
        return;
    }
    push_down(rt,r-l+1);//先向下更新
    int mid=(l+r)>>1;//分成两半继续深入
    if(a<=mid)
        update(a,b,c,lson);
    if(b>mid)
        update(a,b,c,rson);
    push_up(rt);//向上更新
}

以更改[3,6]为例


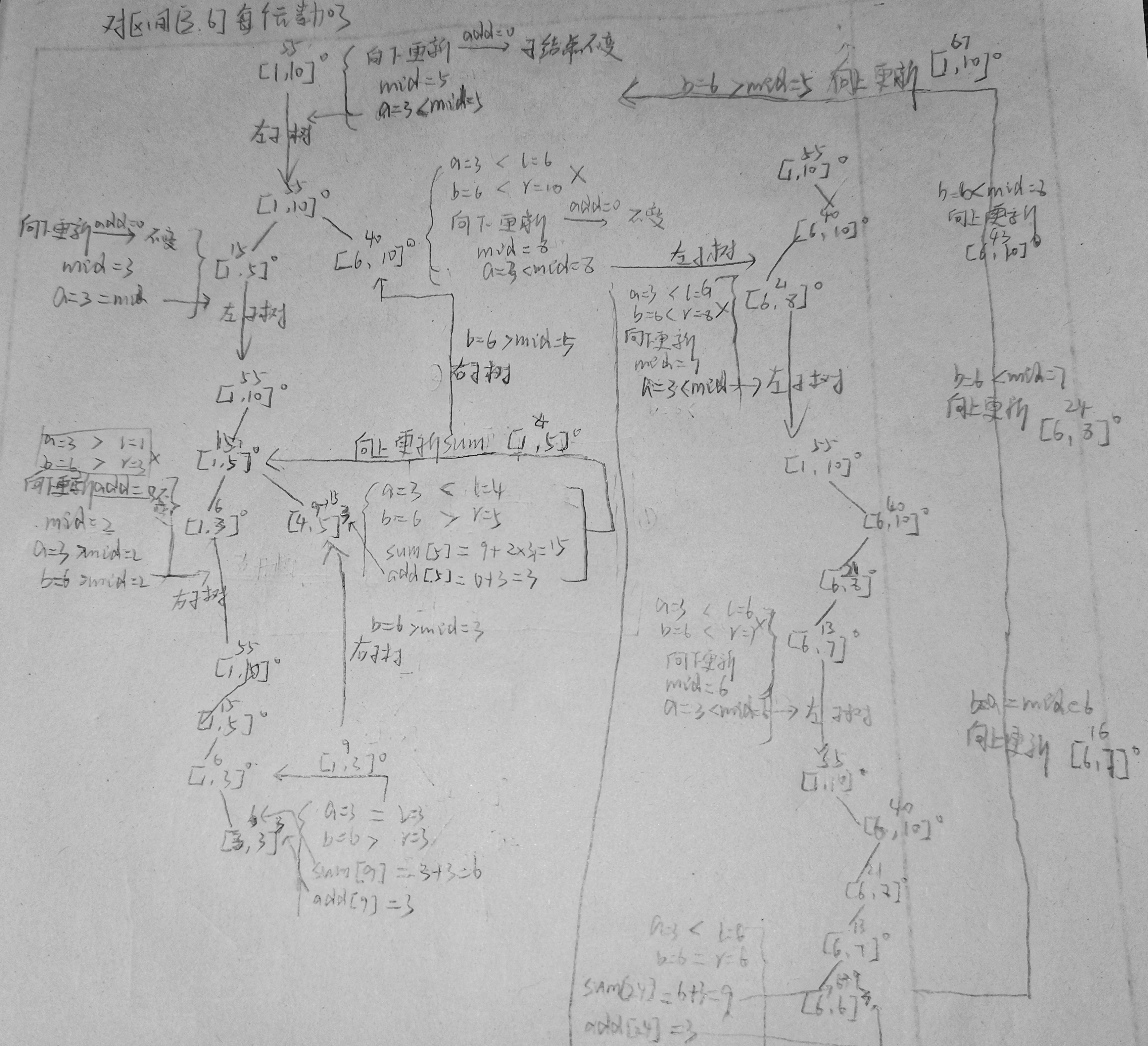
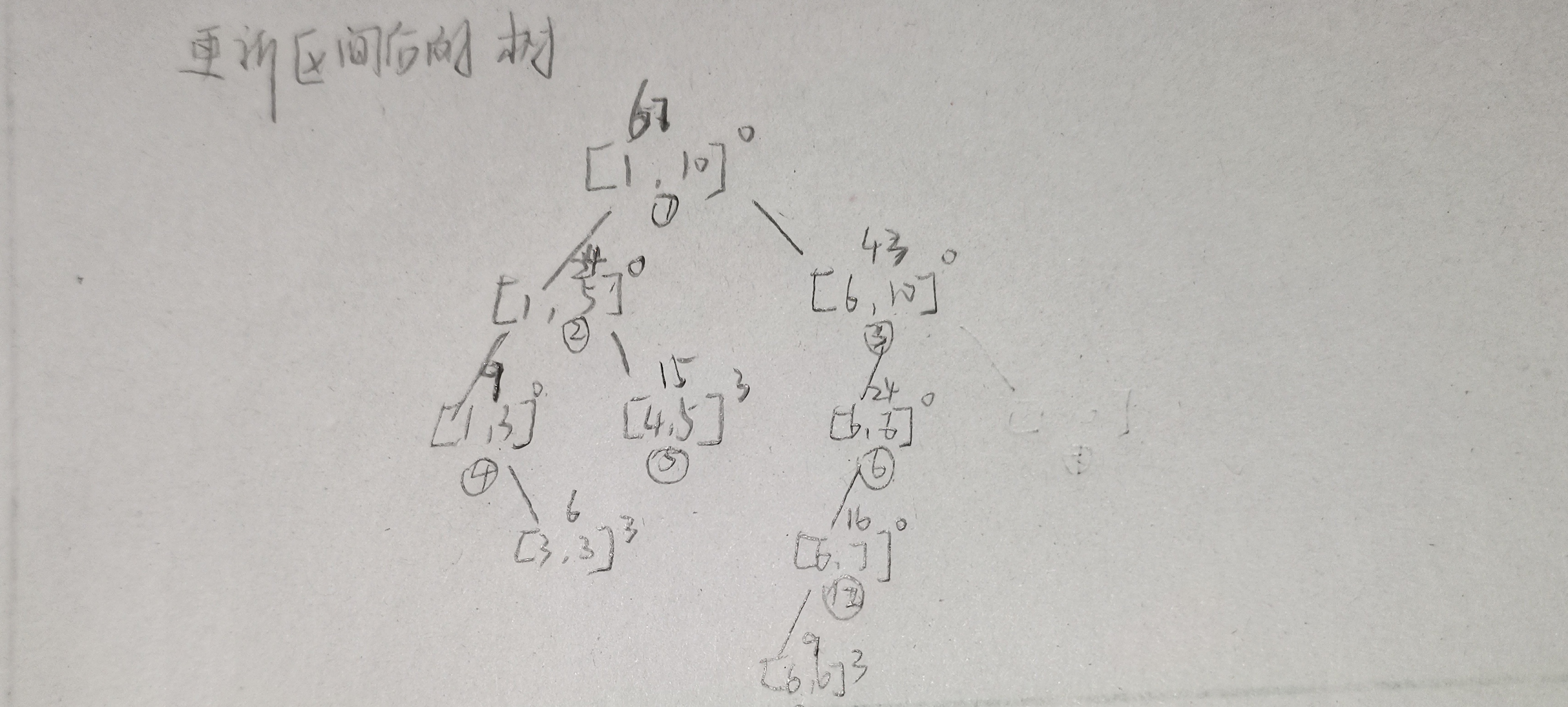
5.区间求和

long long query(int a,int b,int l,int r,int rt)//区间求和
{
    if(a<=l&&b>=r)
        return sum[rt];//满足lazy,直接返回值
    push_down(rt,r-l+1);//向下更新
    int mid=(l+r)>>1;
    long long ans=0;
    if(a<=mid)
        ans+=query(a,b,lson);
    if(b>mid)
        ans+=query(a,b,rson);
    return ans;
}

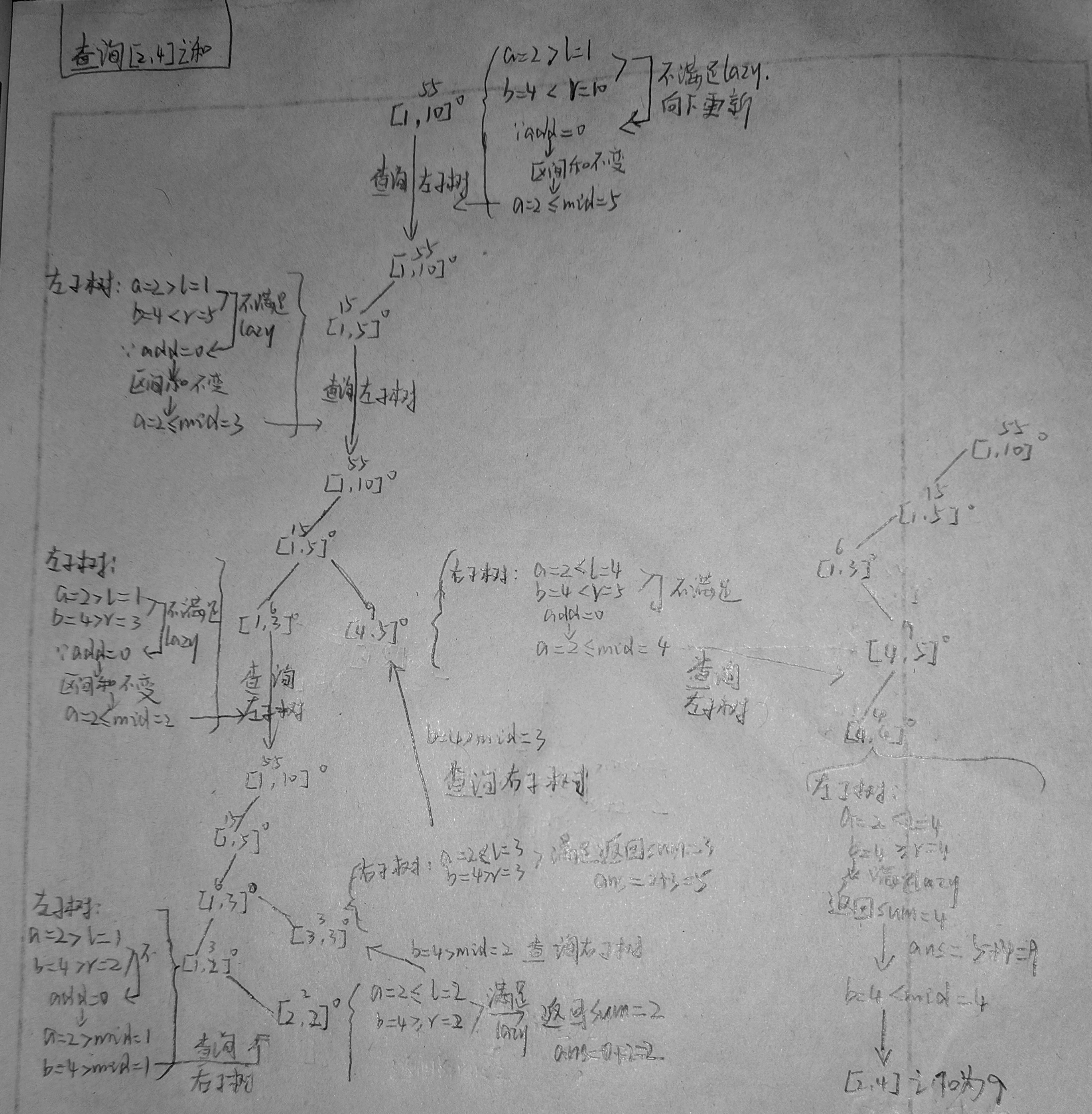
以查询区间[2,4]的和为例：

经典模板题：A Simple Problem with Integers
题意：给你N个数，进行Q个操作
操作1：C a b c：[a,b]内每个元素加c
操作2：Q a b:求：[a,b]区间和

#include<iostream>
#include<cstdio>
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1//这里或运算即rt*2+1
using namespace std;
const int MAXN=1e5+10;
long long sum[MAXN<<2],add[MAXN<<2];//sum[]记录结点的区间和，add[]记录结点是否用到了lazy原理，数组都需要开4倍空间
void push_up(int rt)//向上更新，通过当前结点rt把值递归到父结点
{
    sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}
void push_down(int rt,int m)//更新rt的子结点,m为区间数字的个数
{
    if(add[rt])
    {
        add[rt<<1]+=add[rt];//左儿子累加c
        add[rt<<1|1]+=add[rt];//右儿子累加c
        sum[rt<<1]+=(m-(m>>1))*add[rt];//左儿子区间总和变化
        sum[rt<<1|1]+=(m>>1)*add[rt];//右儿子区间总和变化
        add[rt]=0;//取消本层标记
    }
}
void build(int l,int r,int rt)//满二叉树建树
{
    add[rt]=0;
    if(l==r)
    {
        scanf("%lld",&sum[rt]);
        return;
    }
    int mid=(l+r)>>1;
    build(lson);
    build(rson);
    push_up(rt);//向上更新区间和
}
void update(int a,int b,long long c,int l,int r,int rt)
{
    if(a<=l&&b>=r)
    {
        sum[rt]+=(r-l+1)*c;
        add[rt]+=c;
        return;
    }
    push_down(rt,r-l+1);//先向下更新
    int mid=(l+r)>>1;//分成两半继续深入
    if(a<=mid)
        update(a,b,c,lson);
    if(b>mid)
        update(a,b,c,rson);
    push_up(rt);//向上更新
}
long long query(int a,int b,int l,int r,int rt)//区间求和
{
    if(a<=l&&b>=r)
        return sum[rt];//满足lazy,直接返回值
    push_down(rt,r-l+1);//向下更新
    int mid=(l+r)>>1;
    long long ans=0;
    if(a<=mid)
        ans+=query(a,b,lson);
    if(b>mid)
        ans+=query(a,b,rson);
    return ans;
}
int main()
{
    int N,Q;
    scanf("%d%d",&N,&Q);
    build(1,N,1);
    while(Q--)
    {
        char str[2];//为了空格不影响后面操作
        scanf("%s",str);
        int a,b;
        long long c;
        if(str[0]=='C')
        {
            scanf("%d%d%lld",&a,&b,&c);
            update(a,b,c,1,N,1);
        }
        else{
            scanf("%d%d",&a,&b);
            printf("%lld\\n",query(a,b,1,N,1));
        }
    }
    return 0;
}