2021.8.10提高B组模拟2T3 比赛（二分）（贪心—前缀和）

Posted 2021-09-04 SSL_LKJ

比赛

题目大意

有两个队伍A和B，每个队伍都有n个人。这两支队伍之间进行n场1对1比赛，每一场都是由A中的一个选手与B中的一个选手对抗。同一个人不会参加多场比赛，每个人的对手都是随机而等概率的。例如A队有A1和A2两个人，B队有B1和B2两个人，那么(A1 vs B1,A2 vs B2)和(A1 vs B2,A2 vs B1)的概率都是均等的50%。

每个选手都有一个非负的实力值。如果实力值为X和Y的选手对抗，那么实力值较强的选手所在的队伍将会获得(X-Y)^2的得分。

求A的得分减B的得分的期望值。

输入样例

第一行一个数n表示两队的人数为n。

第二行n个数，第i个数A[i]表示队伍A的第i个人的实力值。

第三行n个数，第i个数B[i]表示队伍B的第i个人的实力值。

2
3 7
1 5

输出样例

输出仅包含一个实数表示A期望赢B多少分。答案保留到小数点后一位（注意精度）。

20.0

题目数据

对于30%的数据，n≤50。

对于100%的.据,n≤50000;A[i],B[i]≤50000。

解题思路

首先答案肯定时两两匹配，结果再除以n

接下来就就是优化

我们可以先将 B 数组进行排序

对于每一个$a_i$有一些操作

在排好序的 B 数组中找到一个位置 k，使左边的数字小于它，右边的数字大于它（二分）

然后左边算（a[] - b[]）的平方，右边算（b[] - a[]）的平方

显然如果暴力做，还是会TLE

那我们就可以用 完全平方公式

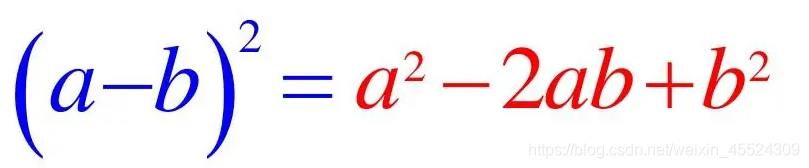
那左边就成了

$$k\ast a_i\ast a_i-a_i\ast （b_1+b_2+\dots \dots +b_k)+（b_1\ast b_1+b_2\ast b_2+\dots \dots +b_k\ast b_k）$$

$b_1$~$b_k$的和 与 $b_1\ast b_1$~ $b_k\ast b_k$的和 可以用前缀和来预处理

就完成优化了

注：记得开 long long 和 特判

AC代码

#include<algorithm>
#include<cstdio>
using namespace std;
long long n,a[50005],b[50005],f[50005],fa[50005];
double ans;
void work(long long x)//二分
{
	long long l=1,r=n,k=0;
	if(a[x]>=b[n])//特判
	{
		ans+=n*a[x]*a[x]-2ll*a[x]*f[n]+fa[n];
		return;
	}
	if(a[x]<=b[1])
	{
		ans-=n*a[x]*a[x]-2ll*a[x]*f[n]+fa[n];
		return;
	}	
	while(l<=r)
	{
		long long mid=(l+r)/2ll;
		if(a[x]>=b[mid])l=mid+1,k=mid;
		else r=mid-1;
	}
	ans+=k*a[x]*a[x]-2ll*a[x]*f[k]+fa[k]-((n-k)*a[x]*a[x]-2ll*a[x]*(f[n]-f[k])+(fa[n]-fa[k]));
}
int main()
{
	scanf("%lld",&n);
	for(long long i=1;i<=n;i++)scanf("%lld",&a[i]);
	for(long long i=1;i<=n;i++)scanf("%lld",&b[i]); 
	sort(b+1,b+n+1);
	for(long long i=1;i<=n;i++)//预处理
	{
		f[i]=f[i-1]+b[i];
		fa[i]=fa[i-1]+b[i]*b[i];
	}
	for(long long i=1;i<=n;i++)work(i);
	printf("%.1lf",ans/(n*1.0));
	return 0;
}

谢谢