折半查找的算法思想实现及其判定树的查找和构造（C语言）

Posted 2021-09-04 bfhonor

一、折半查找

（一）算法思想

• 折半查找，又称“二分查找”，仅适用于有序的顺序表。

1. 查找成功

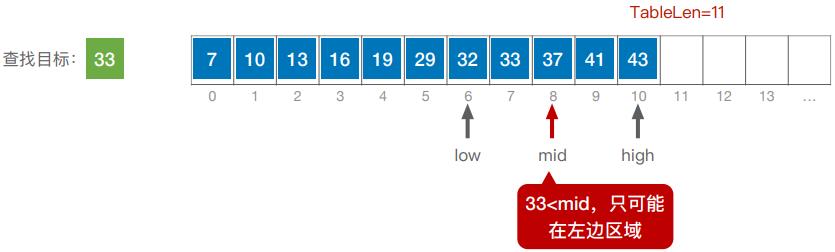
2. 查找失败

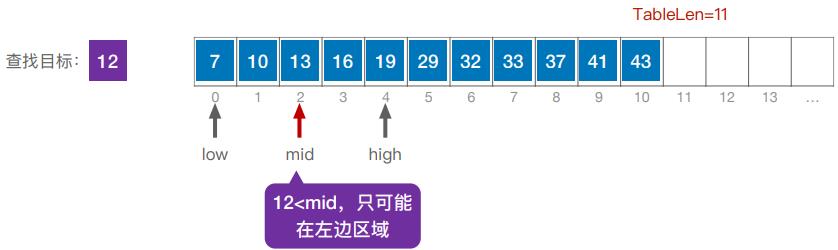
（二）算法实现

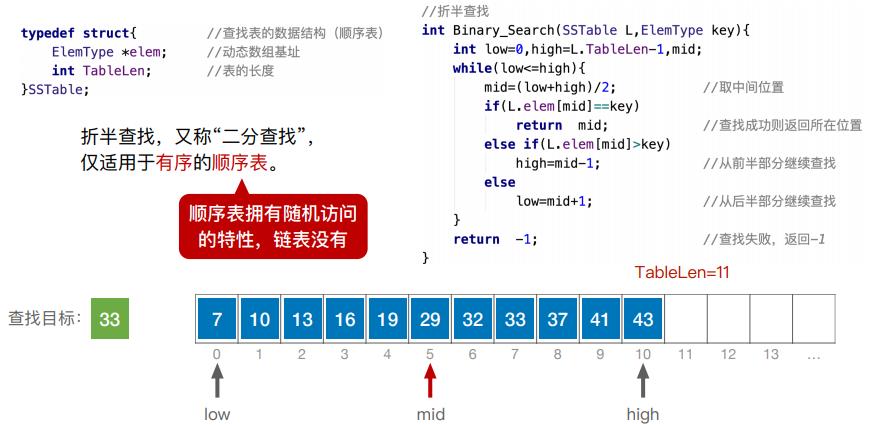
（三）查找判定树

1. 查找效率分析

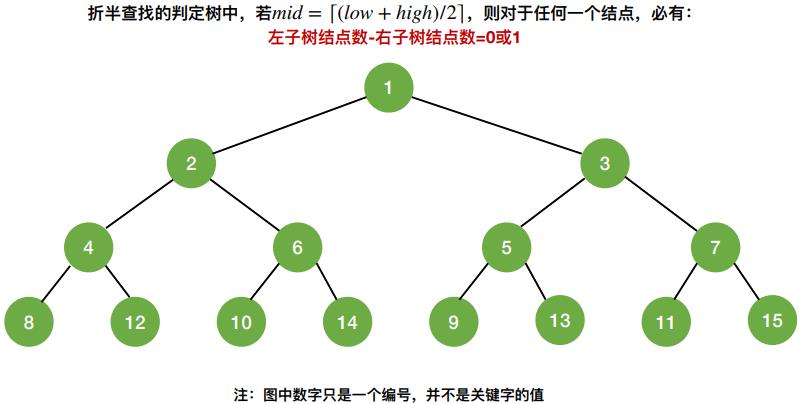
2. 折半查找判定树的构造

• 如果当前low和high之间有奇数个元素，则 mid 分隔后，左右两部分元素个数相等
• mid = ⌊(low + high)/2⌋
  
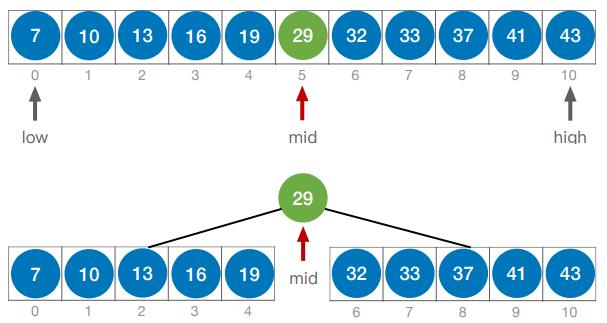
• 如果当前low和high之间有偶数个元素，则 mid 分隔后，左半部分比右半部分少一个元素
• mid = ⌊(low + high)/2⌋
  
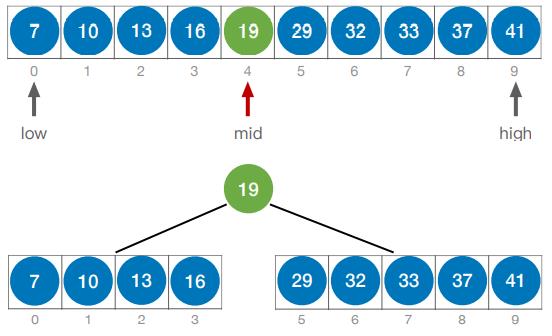
• 如果当前low和high之间有奇数个元素，则 mid 分隔后，左右两部分元素个数相等
• 如果当前low和high之间有偶数个元素，则 mid 分隔后，左半部分比右半部分少一个元素
  
  
  
  
  
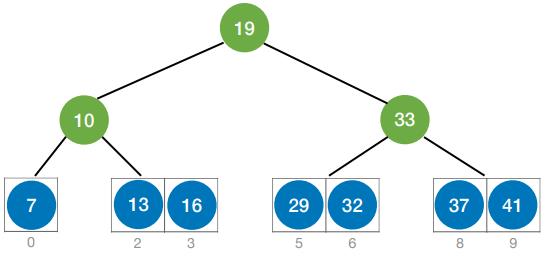
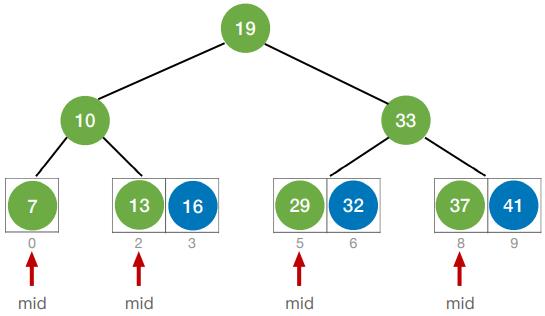
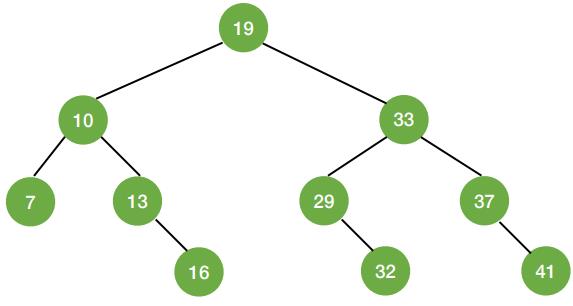
• 折半查找的判定树一定是平衡二叉树
• 折半查找的判定树中，只有最下面一层是不满的。因此，元素个数为n时树高h = ⌈log2(n + 1)⌉
  
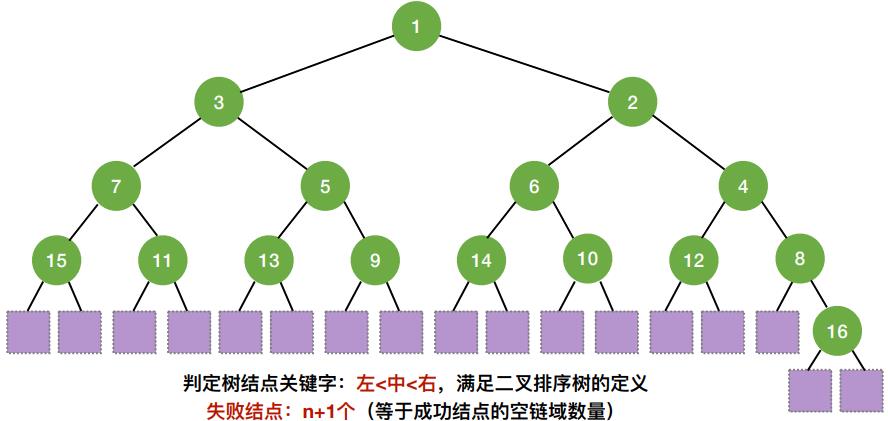
• 判定树结点关键字：左<中<右，满⾜⼆叉排序树的定义；
• 失败结点：n+1个（等于成功结点的空链域数量）

（四）折半查找效率

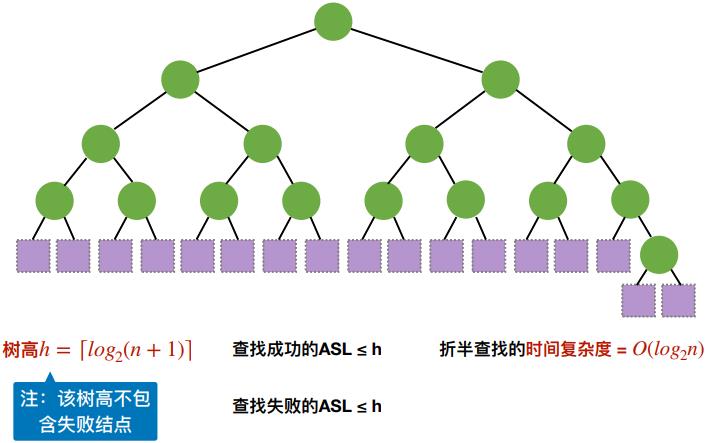
（五）扩展

• 我们通过上面的图即可看出，折半查找不一定比顺序查找更快。因为当查找的元素和顺序表中第一个元素就匹配的时候，顺序查找速度更快。
  
• 如果当前low和high之间有奇数个元素，则 mid 分隔后，左右两部分元素个数相等
• 如果当前low和high之间有偶数个元素，则 mid 分隔后，左半部分比右半部分多一个元素