Jzoj 4257组合数学着色

Posted 2021-09-04 SSL_ZZL

着色

• Link
• 题面
• 解题思路
• • 最基础的思路
  • 两种颜色的特殊
  • 个别图的特殊
• Code

Link

Jzoj【4257】着色

---

题面

Description
有个电子工程系的学生从小喜欢涂颜色。现在他买了本涂色书和K种不同的颜料开始涂色。有趣的是它并不喜欢色彩斑斓的图案，所以一幅图他最多只会用3种不同的颜料。还有，他不会把两个相邻区域涂成同样的颜色。当两个区域的边界至少有一个共同点时两个区域是相邻的。如下图，区域3和4是相邻的，区域1和2不是相邻的。下面的图给出了一种合法的涂色方案。

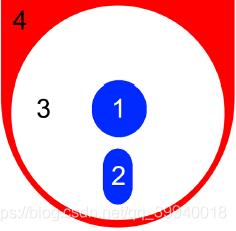
他想知道对于给定的一个图和颜料，有多少种合法的涂色方案。

Input
两个整数N（1<=N<=8），K（1<=K<=1000），N代表他要涂的是书里的第N张图片，K代表有K中不同的颜料选择。
这本书的内容请看后面！！

Output
输出一个整数。代表合法的方案数。

Sample Input
输入1：
2 2
输入2：
5 3
输入3：
7 3

Sample Output
输出1：
0
输出2：
12
输出3：
96

Data Constraint
N（1<=N<=8），K（1<=K<=1000）

Hint

---

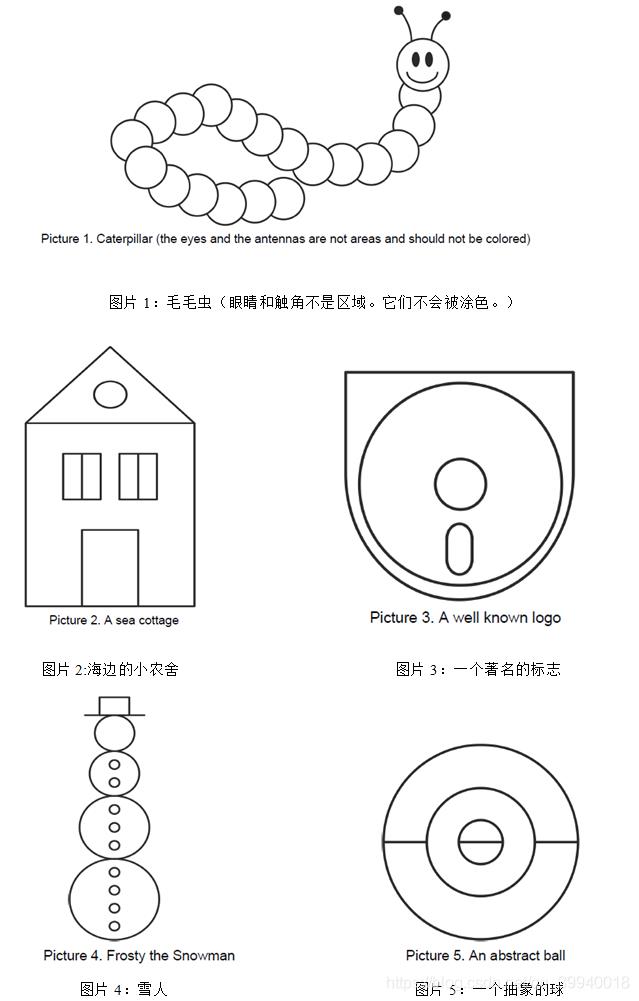
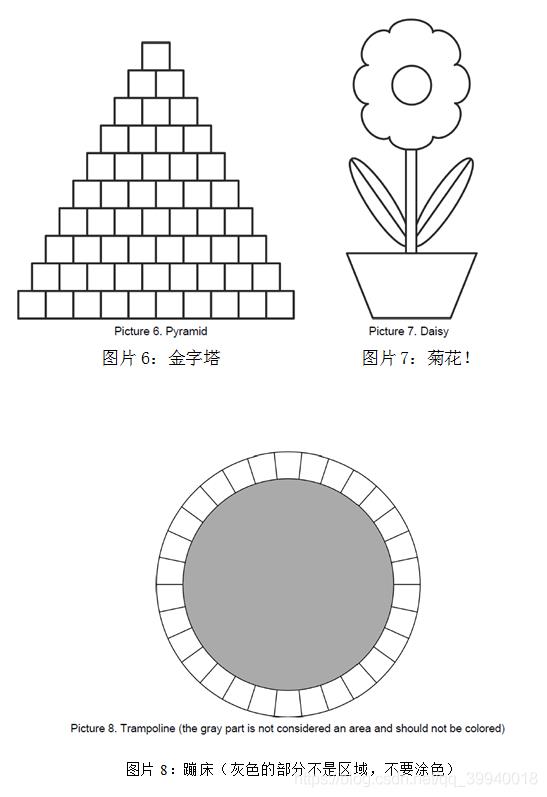
解题思路

一开始没看到一张图最多用三种颜色。。。。。
这题思路很多，很简单就是很长而已，程序短到离谱。。。。

最基础的思路

每个图都简化成一个有向图，有边相连的点不能是同颜色
以图片7为例

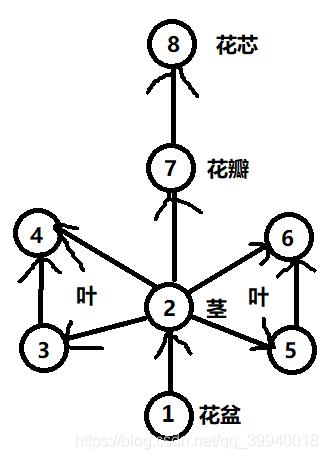
然后每个点都有选颜色的方案数，每个点的方案数 = 3 - 入度数
方案数就是前面的点选了一种颜色，那么这个点有多少种颜色可以选（就是组合数学啦[怒]）

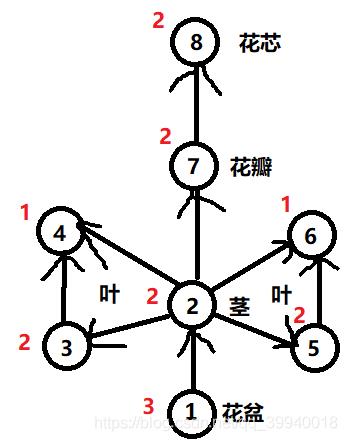
那么这个图用3个颜色的方案数就是3 * 2 * 2 * 2 * 1 * 2 * 1 * 2 * 2 = 96
然后乘上k种颜色中选3种颜色的方案数
剩下的都可以建图推出来

两种颜色的特殊

但是有几个很特殊，可以用2种颜色就可以填出来，比如图片1
那么在3个颜色的方案数中其实包含的2种颜色的方案数

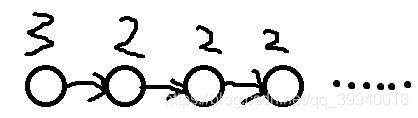
考虑包含了多少2种颜色的方案数
如果是2种颜色，那就是abababab…这样排下去
第一位选一种颜色，3种方案数；第二位选一种颜色，2种方案数；前面两位选定剩下的位就已经固定了
所以其中包含了6个只填了2种颜色的方案数
那就是3 * (2 ^ 19) - 6

那用2种颜色方案数是多少呢？
那其实就是上面的图的数字改一下，颜色种类从3变成了2，方案数就是2 * 1 * 1…

个别图的特殊

图片6
可以发现金字塔建图很麻烦，而且有些点入度为3（！！！）
但其实代入颜色手动填一下，可以发现，顶上的三个选中后，后面的颜色就是固定的了
所以其实就是求顶上三个的方案数

图片8
所有图里最难算的，我直接搞了个暴力dfs求
当然也不是不能建图， 2 * 2 * 2…

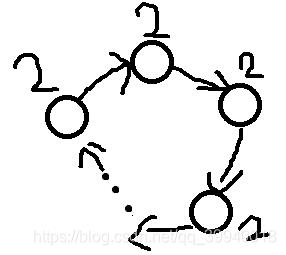
但是起点是有三种颜色可以选，然后分类讨论变得乱七八糟
暴搜yyds

---

Code

#include <iostream>
#include <cstdio>
#define ll unsigned long long

using namespace std;

ll fl[9] = {0, 2, 0, 2, 2, 0, 0, 0, 2};  //填两种颜色的方案数
ll fk[9] = {0, 1572858, 96, 18, 24570, 12, 6, 96, 1073741820};  //填三种颜色的方案数
int n;
ll k, l;

int main() {
	freopen("color.in", "r", stdin);
	freopen("color.out", "w", stdout);
	scanf("%d %lld", &n, &k);
	l = k * (k - 1) / 2;  //k种颜色中选2种颜色
	k = k * (k - 1) * (k - 2) / (ll)6;  //k种颜色中选3种颜色
	printf("%lld", l * fl[n] + fk[n] * k);
}